Download Chapter3-1

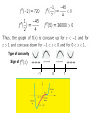
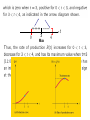
Additional Applications of the
Derivative
Chaper Three
§3.1 Increasing and Decreasing
Function
Increasing and Decreasing Function Let f(x) be a function
defined on the interval a<x<b, and let x1 and x2 be two numbers
in the interval, Then
f(x) is increasing on the interval if f(x2)>f(x1) whenever x2>x1
f(x) is decreasing on the interval if f(x2)<f(x1) whenever x2 >x1
Monotonic
increasing
单调递增
Monotonic
decreasing
单调递减
§3.1 Increasing and Decreasing
Function
Tangent line with positive slope
f(x) will be increasing
f ( x)  0
f ( x)  0
Tangent line with negative slope
f(x) will be decreasing
§3.1 Increasing and Decreasing Function
If f ( x)  0 for every x on some interval I,
then f(x) is increasing on the interval
If f ( x )  0 for every x on some interval I,
then f(x) is decreasing on the interval
If f ( x)  0 for every x on some interval I,
then f(x) is constant on the interval
How to determine all intervals of increase and decrease
for a function ?
How to find all intervals on which the sign
of the derivative does not change.
Intermediate value property
A continuous function cannot change sign without first becoming 0.
§3.1 Increasing and Decreasing
Function
Procedure for using the derivative to determine
intervals of increase and decrease for a function of f.
Step 1. Find all values of x for which f ( x)  0 or f ( x ) is
not continuous, and mark these numbers on a number line.
This divides the line into a number of open intervals.
Step 2. Choose a test number c from each interval a<x<b
determined in the step 1 and evaluate f (c ) . Then
If f (c)  0 the function f(x) is increasing on a<x<b.
If f (c)  0 the function f(x) is decreasing on a<x<b
Example. Find the intervals of increase and decrease for the
function
f ( x)  2 x3  3x 2  12 x  7
Solution:
f ( x)  6 x 2  6 x  12  6( x  2)( x  1)
Which is continuous everywhere, with f ( x)  0 where x=1 and x=-2
The number -2 and 1 divide x axis into three open intervals.
x<-2, -2<x<1 and x>1
Interval
Test
number
Conclusion
f (c )
Direction
of graph
x<-2
-3
f ( 3)  0 f is increasing
Rising
-2<x<1
0
f (0)  0 f is deceasing
Falling
x>1
2
f (2)  0 f is increasing
Rising
§3.1 Relative Extrema
Relative (Local) Extrema The Graph of the function f(x) is said
to be have a relative maximum at x=c if f(c)  f(x) for all x in
interval a<x<b containing c. Similarly the graph has a relative
Minimum at x=c if f(c)  f(x) on such an interval. Collectively,
the relative maxima and minima of f are called its relative extrema
Peaks: C,E,
(Relative maxima)
Valleys: B, D, G
(Relative minima)
§3.1 Critical Points
Critical Numbers and Critical Points
A number c in the
domain of f(x) is called a critical number if either f (c)  0 or
f (c ) does not exist. The corresponding point (c,f(c)) on the graph
of f(x) is called a critical point for f(x).
Relative extrema can only occur at critical points!
§3.1 Critical Points
Not all critical points correspond to relative extrema!
Figure. Three critical points where f’(x) = 0:
(a) relative maximum, (b) relative minimum
(c) not a relative extremum.
§3.1 Critical Points
Not all critical points correspond to relative extrema!
Figure Three critical points where f’(x) is undefined:
(a) relative maximum, (b) relative minimum
(c) not a relative extremum.
§3.1 The First Derivative Test
The First Derivative Test for Relative Extrema
Let c be a critical number for f(x) [that is, f(c) is defined
and either f ( x)  0 or f (c ) does not exist]. Then the critical
point (c,f(c)) is
A relative maximum
if f ( x)  0 to
the left of c and f ( x)  0 to the right of c
A relative minimum
if f ( x)  0 to
the left of c and f ( x)  0 to the right of c
Not a relative extremum if f ( x )
has the same sign on both sides of c
f0 c
f0
f0 c
f0 c f0
f0
f0
c
f0
Example Find all critical numbers of the function
f ( x)  2 x 4  4 x 2  3
and classify each critical point as a relative maximum, a relative
minimum, or neither
Solution
f ( x)  8x3  8x  8x( x 1)( x  1)
The derivative exists for all x, the only critical numbers are
Where f ( x)  0 that is, x=0,x=-1,x=1. These numbers
divide that x axis into four intervals, x<-1, -1<x<0, 0<x<1, x>1
Choose a test number in each of these intervals
f (5)  960  0
1
f ( )  3  0
2
-------- ++++++ -------- +++++
+
-1 min
0 max
1 min
1
15
f ( )    0
4
8
f (2)  48  0
Thus the graph of f falls for x<-1 and for
0<x<1, and rises for -1<x<0 and for x>1
x=0 relative maximum
x=1 and x=-1 relative minimum
§3.1 Sketch the graph
A Procedure for Sketching the Graph of a Continuous
Function f(x) Using the Derivative
Step 1. Determine the domain of f(x).
Step 2. Find f ( x) and each critical number, analyze the sign of
derivative to determine intervals of increase and decrease for f(x).
Step 3. Plot the critical point P(c,f(c)) on a coordinate plane,
with a “cap”
at P if it is a relative maximum or a “cup”
if P is a relative minimum. Plot intercepts and other key points that
can be easily found.
Step 4 Sketch the graph of f as a smooth curve joining the critical
points in such way that it rise where f ( x)  0, falls where f ( x)  0
and has a horizontal tangent where f ( x)  0
Example
Sketch the graph of the function
f ( x)  x 4  8x3  18x 2  8
Solution
f ( x)  4 x3  24 x 2  36 x  4 x( x  3)2
The derivative exists for all x, the only critical numbers are
Where f ( x)  0 that is, x=0, x=-3. These numbers divide
that x axis into three intervals, x<-3, -3<x<0, x>0.
Choose test number in each interval (say, -5, -1 and 1 respectively)
f (5)  80  0
--------
--------
-3
neither
++++++
0
min
f (1)  16  0 f (1)  64  0
Thus the graph of f has a horizontal
tangents where x is -3 and 0, and it is
falling in the interval x<-3 and -3<x<0
and is rising for x>0
f(-3)=19 f(0)=-8
Plot a “cup”
at the critical point (0,-8)
Plot a “twist”
at (-3,19) to indicate a galling graph with
a horizontal tangent at this point .
Complete the sketch by passing a smooth curve through the
Critical point in the directions indicated by arrow
Example The revenue derived from the sale of a new kind of
motorized skateboard t weeks after its introduction is given by
63t  t 2
R(t )  2
t  63
million dollars. When does maximum revenue occur? What is
the maximum revenue
Solution
Critical number t=7 divides the domain
0  t  63 into two intervals x<=t<7
63(7)  (7)2
and 7<t<=63
R(7) 
++++++ -------7
63
0
Max
(7)  63
2
t
 3.5
§3.2 Concavity
Increase and decrease of the slopes are our concern!
Figure The output Q(t) of a factory worker t hours after coming to work.
§3.2 Concavity
Concavity
If the function f(x) is differentiable on the interval
a<x<b then the graph of f is
Concave upward on a<x<b if f ( x ) is increasing on the interval
Concave downward on a<x<b if f ( x ) is decreasing on the interval
§3.2 Concavity
A graph is concave upward on the interval if it lies above all its
tangent lines on the interval and concave downward on an
Interval where it lies below all its tangent lines.
Note Don’t confuse the concavity of a graph with its “direction”
(rising or falling). A function may be increasing or decreasing on
an interval regardless of whether its graph is concave upward or
concave downward on the interval.
§3.2 Concavity and the second
Derivative
How to characterize the concavity of the graph of function f(x)
in terms of the second derivative?
A function f(x) is increasing where its derivative is positive. Thus, the
derivative function f ( x ) must be increasing where its derivative f ( x ) is
positive. Similarly, on interval a<x<b, where f ( x )  0 , the derivative f ( x )
will be decreasing.
§3.2 Concavity and the second
Derivative
Second Derivative Procedure for Determining Intervals of
Concavity for a Function f.
Step 1. Find all values of x for which f ( x )  0 or f ( x ) is
not continuous, and mark these numbers on a number line.
This divides the line into a number of open intervals.
Step 2. Choose a test number c from each interval a<x<b
determined in the step 1 and evaluate f (c ). Then
If f (c )  0 , the graph of f(x) is concave upward on a<x<b.
If f (c )  0 the graph of f(x) is concave downward on a<x<b
to be continued
Type of concavity
Sign of
++++++
-1
--------
-------0
++++++
1
§3.2 Inflection points
Type of concavity
Sign of
--------
--------
0
No inflection
++++++
1
inflection
to be continued
Type of concavity
Sign of
++++++
-------
0
inflection
Note: A function can have an inflection point only where it
is continuous.!!
§3.2 Behavior of Graph f(x) at an
inflection point P(c,f(c))
--------
++++++
-1.5
min
++++++
1
Neither
to be continued
Type of concavity
Sign of
++++++
--------
-2/3
inflection
++++++
1
inflection
to be continued
Review
a.
b. Find all critical numbers of the function
c. Classify each critical point as a relative maximum, a
relative minimum, or neither
d.
e. Find all inflection points of function
to be continued
++++++
--------
--------
++++++
to be continued
--------
++++++
--------
++++++
to be continued
§3.2 The Second Derivative Test
to be continued
++++++ -------3
4
0
Max
t