Download Chapter 5 Sect. 1,2,3 - Columbus State University

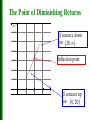
Chapter 5
Applications of the
Derivative
Sections 5.1, 5.2, 5.3, and 5.4
Applications of the Derivative
 Maxima and Minima
 Applications of Maxima and Minima
 The Second Derivative - Analyzing Graphs
Absolute Extrema
Let f be a function defined on a domain D
Absolute
Maximum
Absolute
Minimum
Absolute Extrema
A function f has an absolute (global) maximum at
x = c if f (x)  f (c) for all x in the domain D of f.
The number f (c) is called the absolute maximum
value of f in D
Absolute
Maximum
f (c )
c
Absolute Extrema
A function f has an absolute (global) minimum at
x = c if f (c)  f (x) for all x in the domain D of f.
The number f (c) is called the absolute minimum
value of f in D
c
f (c )
Absolute
Minimum
Generic Example
y
8
7
6
5
4
3
2
1
x
-3
-2
-1
1
-1
2
3
4
5
6
Generic Example
y
8
7
6
5
4
3
2
1
x
-3
-2
-1
1
-1
2
3
4
5
6
Generic Example
y
8
7
6
5
4
3
2
1
x
-3
-2
-1
1
-1
2
3
4
5
6
Relative Extrema
A function f has a relative (local) maximum at x  c if
there exists an open interval (r, s) containing c such
that f (x)  f (c) for all r  x  s.
Relative
Maxima
Relative Extrema
A function f has a relative (local) minimum at x  c if
there exists an open interval (r, s) containing c such
that f (c)  f (x) for all r  x  s.
Relative
Minima
Generic Example
y
8
f ( x)  0
7
6
5
4
3
f ( x)  DNE
2
1
x
-3
-2
-1
1
2
3
4
5
6
-1
The corresponding values of x are called
Critical Points of f
Critical Points of f
A critical number of a function f is a number c in
the domain of f such that
a. f (c)  0 (stationary point)
b. f (c ) does not exist (singular point)
Candidates for Relative Extrema
1.Stationary points: any x such that x is in
the domain of f and f '(x)  0.
2.Singular points: any x such that x is in the
domain of f and f '(x)  undefined
3. Remark: notice that not every critical number
correspond to a local maximum or local minimum.
We use “local extrema” to refer to either a max or
a min.
Fermat’s Theorem
If a function f has a local maximum or minimum
at c, then c is a critical number of f
Notice that the theorem does not say that at every
critical number the function has a local maximum or
local minimum
Generic Example
y
8
f ( x)  0
7
not a local extrema
6
5
4
3
f ( x)  DNE
2
not a local extrema
1
x
-3
-2
-1
1
2
3
4
5
6
-1
Two critical points of f that do
not correspond to local extrema
Example
Find all the critical numbers of
f ( x)  3 x 3  3 x .
x2 1
f ( x) 
3
x
3
 3x

2
Stationary points: x  1
Singular points: x  0,  3
Graph of f ( x)  x  3 x .
3
3
y
Local max. f (1)  3 2
2
1
x
-2
-1
1
2
3
-1
-2
-3
Local min. f (1)   3 2
Extreme Value Theorem
If a function f is continuous on a closed interval [a,b],
then f attains an absolute maximum and absolute
minimum on [a, b]. Each extremum occurs at a critical
number or at an endpoint.
a
b
Attains max.
and min.
a
b
a
b
Attains min.
but no max.
No min. and
no max.
Open Interval
Not continuous
Finding absolute extrema on [a , b]
1. Find all critical numbers for f (x) in (a,b).
2. Evaluate f (x) for all critical numbers in (a,b).
3. Evaluate f (x) for the endpoints a and b of the
interval [a,b].
4. The largest value found in steps 2 and 3 is the
absolute maximum for f on the interval [a , b],
and the smallest value found is the absolute
minimum for f on [a,b].
Example
 1 
Find the absolute extrema of f ( x)  x  3 x on   ,3 .
 2 
2
f ( x)  3x  6 x  3x( x  2)
3
2
Critical values of f inside the interval (-1/2,3) are x = 0, 2
Evaluate
f (0)  0
Absolute Max.
f (2)  4
Absolute Min.
7
 1
f    
8
 2
f  3  0
Absolute Max.
Example
 1 
Find the absolute extrema of f ( x)  x  3 x on   ,3 .
 2 
3
2
Critical values of f inside the interval (-1/2,3) are x = 0, 2
Absolute Max.
-2
-1
1
2
3
4
5
6
Absolute Min.
-5
Example
 1 
Find the absolute extrema of f ( x)  x  3x on   ,1 .
 2 
2
f ( x)  3x  6 x  3x( x  2)
3
2
Critical values of f inside the interval (-1/2,1) is x = 0 only
Evaluate
f (0)  0
Absolute Max.
7
 1
f    
8
 2
f 1  2
Absolute Min.
Example
 1 
Find the absolute extrema of f ( x)  x  3x on   ,1 .
 2 
2
f ( x)  3x  6 x  3x( x  2)
3
2
Critical values of f inside the interval (-1/2,1) is x = 0 only
Absolute Max.
-2
-1
1
2
3
4
5
6
Absolute Min.
-5
Increasing/Decreasing/Constant
y
8
7
6
5
4
3
2
1
x
-3
-2
-1
1
-1
2
3
4
5
6
Increasing/Decreasing/Constant
y
8
7
6
5
4
3
2
1
x
-3
-2
-1
1
-1
2
3
4
5
6
Increasing/Decreasing/Constant
If f  x   0 for each value of x in an interval a, b ,
then f is increasing on a, b .
If f x   0 for each value of x in an interval a, b ,
then f is decreasing on a, b .
If f  x   0 for each value of x in an interval a, b ,
then f is constant on a, b .
The First Derivative Test
Generic Example
y
A similar
Observation
Applies at a
Local Max.
8
7
6
5
4
3
2
f ( x)  0
1
to the left of c
x
c
-3
-2
-1
1
-1
2
3
4
f ( x)  0
to the right of c
5
6
The First Derivative Test
Determine the sign of the derivative of f to
the left and right of the critical point.
left
right




No change
conclusion
f (c) is a relative maximum
f (c) is a relative minimum
No relative extremum
Relative Extrema
Example: Find all the relative extrema of
f ( x)  x  6 x  1
3
Stationary points:
2
2

f ( x)  3x  12 x  0
x  0, 4
Singular points: None
The First Derivative Test
Find all the relative extrema of f ( x)  x3  6 x 2  1.
f ( x)  3x 2  12 x  0
3x( x  4)  0
x  0, 4
Relative max.
f (0) = 1
f
f
+
0
0
-
0
4
Relative min.
f (4) = -31
+
The First Derivative Test
y
5
(0,f(0)=1)
-2
-1
1
2
x
3
4
5
6
7
-5
-10
-15
-20
-25
-30
(4,f(4)=-31)
-35
8
9
10
The First Derivative Test
y
5
(0,f(0)=1)
-2
-1
1
2
x
3
4
5
6
7
-5
-10
-15
-20
-25
-30
(4,f(4)=-31)
-35
8
9
10
Another Example
Find all the relative extrema of
f ( x)  3 x 3  3 x .
x 1
2
f ( x) 
3
x
3
 3x

2
Stationary points: x  1
Singular points: x  0,  3
Stationary points: x  1
Singular points: x  0,  3
Relative max.
Relative min.
f ( 1)  3 2
f (1)   3 2
f +
f
ND + 0
 3
-1
-
ND
0
-
0
+ ND +
1
3
Graph of f ( x)  x  3 x .
3
3
y
Local max. f (1)  3 2
2
1
x
-2
-1
1
2
3
-1
-2
-3
Local min. f (1)   3 2
Domain Not a Closed Interval
Example: Find the absolute extrema of
1
f ( x) 
on 3,  .
 x  2
Notice that the interval is not closed. Look graphically:
Absolute Max.
(3, 1)
Optimization Problems
1. Identify the unknown(s). Draw and label a diagram as
needed.
2. Identify the objective function. The quantity to be
minimized or maximized.
3. Identify the constraints.
4. State the optimization problem.
5. Eliminate extra variables.
6. Find the absolute maximum (minimum) of the
objective function.
Optimization - Examples
An open box is formed by cutting identical squares from
each corner of a 4 in. by 4 in. sheet of paper. Find the
dimensions of the box that will yield the maximum
volume.
x
4 – 2x
x
x 4 – 2x x
V  lwh  (4  2x)(4  2x) x ; x in 0, 2
V  x   16 x 16 x2  4 x3
V ( x)  16  32 x  12 x 2
 4(2  3 x)(2  x)
2
both in [0, 2]
Critical points: x  2,
3
V (2)  0
V (0)  0
2
V    4.74 in 3
3
The dimensions are 8/3 in. by 8/3 in. by 2/3 in. giving
a maximum box volume of V  4.74 in3.
Optimization - Examples
An metal can with volume 60 in3 is to be constructed
in the shape of a right circular cylinder. If the cost of
the material for the side is $0.05/in.2 and the cost of
the material for the top and bottom is $0.03/in.2 Find
the dimensions of the can that will minimize the cost.
V   r h  60
2
C  (0.03)(2) r 2  (0.05)2 rh
cost
top and
bottom
side
V   r h  60
2
60
So h  2
r
C  (0.03)(2) r 2  (0.05)2 rh Sub. in for h
60
2
 (0.03)(2) r  (0.05)2 r 2
r
6
2
 0.06 r 
r
6
C   0.12 r  2
r
6
C   0 gives 0.12 r  2
r
6
3
r
 2.52 in. which yields h  3.02 in.
0.12
Graph of cost function to verify absolute minimum:
2.5
So with a radius ≈ 2.52 in. and height ≈ 3.02 in.
the cost is minimized at ≈ $3.58.
Second Derivative
If y  f ( x) is a function of x, then the function
y  f ( x) denotes the first derivative of f ( x).
Now, the derivative of y  f ( x) is denoted by
y  f ( x) and called the second derivative of
the function y  f ( x).
d2 f
Notation: f ( x) is also denoted by
dx2
Second Derivative - Example
Given s(t )  130  15t  8t
2
s(t )  30t  24t
3
find s(2).
2
s(t )  30  48t
then, s(2)  30  48(2)  66
Second Derivative
In both cases f is increasing. However, in the first case
f curves down and in the second case f curves up.
Second Derivative
f ( x ) is
f ( x ) is
f ( x) is
so, f ( x)  0
f ( x) is
so, f ( x)  0
Concavity
Let f be a differentiable function on (a, b).
1. f is concave upward on (a, b) if f ' is increasing on
aa(a, b). That is f ''(x)  0 for each value of x in (a, b).
2. f is concave downward on (a, b) if f ' is decreasing
on (a, b). That is f ''(x)  0 for each value of x in (a, b).
concave upward
concave downward
Inflection Point
A point on the graph of f at which f is continuous
and concavity changes is called an inflection point.
To search for inflection points, find any point, c in the
domain where f ''(x)  0 or f ''(x) is undefined.
If f '' changes sign from the left to the right of c, then
(c,f (c)) is an inflection point of f.
Example: Inflection Points
Find all inflection points of
f ( x)  x  6 x  1.
2

f ( x)  3x  12 x
3
2
f ( x)  6 x  12
Possible inflection points are solutions of
a) f ( x)  0
b) f ( x)  DNE
6 x  12  0
no solutions
x2
Inflection
point at x  2
f 
f
-
0
2
+
y
5
(0,f(0)=1)
-2
-1
1
2
x
3
4
5
6
7
-5
-10
-15
-20
-25
-30
(4,f(4)=-31)
-35
8
9
10
The Point of Diminishing Returns
If the function S (t )  100  60t 2  t 3 represents the
total sales of a particular object, t months after being
introduced, find the point of diminishing returns.
S (t )  120t  3t
S concave up
on  0, 20 
2
S (t )  120  6t
S concave down
on  20, 
The point of diminishing returns is at 20 months
(the rate at which units are sold starts to drop).
The Point of Diminishing Returns
S(t)
30000
S concave down
on  20, 
25000
20000
Inflection point
15000
10000
5000
t
10
20
30
40
S concave up
on  0, 20 