Download Tanabe-Sugano Diagram Jahn-Teller Effect

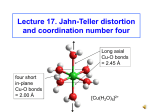
4/8/2012
Tanabe-Sugano Diagram
Jahn-Teller Effect
In order to accurately interpret the electronic spectra
of transition metal complexes, a series of diagrams
have been created.
These diagrams are used to assign transitions (initial
energy state and final energy state) to peaks observed
in the spectra, and to calculate the value of ∆o.
Tanabe-Sugano diagrams have the lowest energy
state (the ground state) plotted along the horizontal
axis. The energy of excited states can then be readily
compared to the ground state.
Yuniar Ponco Prananto
Tanabe-Sugano diagrams are used in coordination chemistry to
predict absorptions in the UV and visible electromagnetic
spectrum of coordination compounds.
The results from a Tanabe-Sugano diagram analysis of a metal
complex can also be compared to experimental spectroscopic
data. They are qualitatively useful and can be used to
approximate the value of 10Dq, the ligand field splitting energy.
Tanabe-Sugano diagrams can be used for both high spin and low
spin complexes.
Tanabe-Sugano diagrams can also be used to predict the size of
the ligand field necessary to cause high-spin to low-spin
transitions.
In a Tanabe-Sugano diagram, the ground state is used as a
constant reference. The energy of the ground state is taken to be
zero for all field strengths, and the energies of all other terms
and their components are plotted with respect to the ground
term.
The x-axis of a Tanabe-Sugano diagram is expressed in terms
of the ligand field splitting parameter, Dq, or Δ, divided by the
Racah parameter B. The y-axis is in terms of energy, E, also
scaled by B.
Three Racah parameters exist, A, B, and C, which describe
various aspects of interelectronic repulsion. A is an average
total interelectron repulsion. A is constant among d-electron
configuration, and it is not necessary for calculating relative
energies, hence its absence from Tanabe and Sugano's studies
of complex ions. B and C correspond with individual delectron repulsions. C is necessary only in certain cases. B is
the most important of Racah's parameters in this case.
One line corresponds to each electronic state. The bending of
certain lines is due to configuration interactions of the excited
states.
1
4/8/2012
Hund’s Rules
Although electronic transitions are only "allowed" if the spin
multiplicity remains the same (i.e. electrons do not change
from spin up to spin down or vice versa when moving from
one energy level to another), energy levels for "spinforbidden" electronic states are included in the diagrams.
Each state is given its symmetry label (e.g. A1g, T2g, etc.), but
"g" and "u" subscripts are usually left off because it is
understood that all the states are gerade. Labels for each
state are usually written on the right side of the table,
though for more complicated diagrams (e.g. d6) labels may
be written in other locations for clarity.
Term symbols (e.g. 3P, 1S, etc.) for a specific dn free ion are
listed, in order of increasing energy, on the y-axis of the
diagram. The relative order of energies is determined using
Hund's rules.
In atomic physics, Hund's rules refer to a set of rules formulated by German
physicist Friedrich Hund around 1927, which are used to determine the
term symbol that corresponds to the ground state of a multi-electron atom.
In chemistry, rule one is especially important and is often referred to as
simply Hund's rules.
The three rules are:
For a given electron configuration, the term with maximum multiplicity
has the lowest energy. Since multiplicity is 2S+1 equal to , this is also the
term with maximum S. S is the spin angular momentum.
For a given multiplicity, the term with the largest value of L has the
lowest energy, where L is the orbital angular momentum.
For a given term, in an atom with outermost sub-shell half-filled or less,
the level with the lowest value of J lies lowest in energy. If the outermost
shell is more than half-filled, the level with highest value of J is lowest in
energy. J is the total angular momentum, J = L + S.
These rules specify in a simple way how the usual energy
interactions dictate the ground state term. The rules assume
that the repulsion between the outer electrons is very much
greater than the spin-orbit interaction which is in turn
stronger than any other remaining interactions. This is
referred to as the LS coupling regime.
Full shells and sub-shells do not contribute to the quantum
numbers for total S, the total spin angular momentum and for
L, the total orbital angular momentum. It can be shown that
for full orbitals and sub-orbitals both the residual electrostatic
term (repulsion between electrons) and the spin-orbit
interaction can only shift all the energy levels together. Thus
when determining the ordering of energy levels in general
only the outer valence electrons need to be considered.
Splitting of Term Symbols from Spherical to Octahedral Symmetry
Term
S
P
D
F
G
H
I
Degeneracy States in an octahedral field
1
A1g
3
T1g
5
Eg + T2g
7
A2g + T1g + T2g
9
A1g + Eg + T1g + T2g
11
Eg + T1g + T1g + T2g
13
A1g + A2g + Eg + T1g + T2g + T2g
2
4/8/2012
Certain Tanabe-Sugano diagrams (d4, d5, d6, and d7) also have
a vertical line drawn at a specific Dq/B value, which
corresponds with a discontinuity in the slopes of the excited
states' energy levels. This pucker in the lines occurs when the
spin pairing energy, P, is equal to the ligand field splitting
energy, Dq.
Complexes to the left of this line (lower Dq/B values) are
high-spin, while complexes to the right (higher Dq/B values)
are low-spin.
There is no low-spin or high-spin designation for d2, d3, or d8.
d4
--electron configurations--
d5
d2
--electron configurations--
d3
d6
--electron configurations--
d7
3
4/8/2012
Unnecessary diagrams: d1, d9 and d10
d1
There is no electron repulsion in a d1 complex, and the single electron
resides in the t2g orbital ground state. A d1 octahedral metal complex, such
as [Ti(H2O)6]3+, shows a single absorption band in a UV-vis experiment. The
term symbol for d1 is 2D, which splits into the 2T2g and 2Eg states. The t2g
orbital set holds the single electron and has a 2T2g state energy of -4Dq.
When that electron is promoted to an eg orbital, it is excited to the 2Eg
state energy, +6Dq. This is in accordance with the single absorption band
in a UV-vis experiment. Thus, this simple transition from 2T2 to 2Eg does
not require a Tanabe-Sugano diagram.
d8 electron configurations
• d9
Similar to d1 metal complexes, d9 octahedral metal complexes have 2D spectral
term. The transition is from the (t2g)6(eg)3 configuration (2Eg state) to the
(t2g)5(eg)4 configuration (2T2g state). This could also be described as a positive
"hole" that moves from the eg to the t2g orbital set. The sign of Dq is opposite
that for d1, with a 2Eg ground state and a 2T2g excited state. Like the d1 case, d9
octahedral complexes do not require the Tanabe-Sugano diagram to predict
their absorption spectra.
Applications as a qualitative tool
In a centrosymmetric ligand field, such as in octahedral complexes of transition
metals, the arrangement of electrons in the d-orbital is not only limited by
electron repulsion energy, but it is also related to the splitting of the orbitals due
to the ligand field. This leads to many more electron configuration states than is
the case for the free ion. The relative energy of the repulsion energy and
splitting energy defines the high-spin and low-spin states.
Considering both weak and strong ligand fields, a Tanabe-Sugano diagram shows
the energy splitting of the spectral terms with the increase of the ligand field
strength. It is possible for us to understand how the energy of the different
configuration states is distributed at certain ligand strengths. The restriction of
the spin selection rule makes it is even easier to predict the possible transitions
and their relative intensity.
• d10
There are no d-d electron transitions in d10 metal complexes because the d
orbitals are completely filled. Thus, UV-vis absorption bands are not observed
and a Tanabe-Sugano diagram does not exist.
Although they are qualitative, Tanabe-Sugano diagrams are very useful tools for
analyzing UV-vis spectra: they are used to assign bands and calculate Dq values
for ligand field splitting.
4
4/8/2012
Note:
Interpretation of Spectra – d3 and d8
Tanabe-Sugano diagrams are utilized in determining electron
placements for high spin and low spin metal complexes.
However, they are limited in that they have only qualitative
significance. Even so, Tanabe-Sugano diagrams are useful in
interpreting UV-vis spectra and determining the value of 10Dq.
Tetrahedral Tanabe-Sugano diagrams are not commonly found
in textbooks because ΔT for tetrahedral complexes is
approximately 4/9 of ΔO for an octahedral complex. The
consequence of the magnitude of ΔT results in the tetrahedral
complexes being high spin.
Orgel diagrams are best used for the treatment of tetrahedral
complexes.
Interpretation of Spectra – d3 and d8
ν1
The Tanabe-Sugano diagram can be used to assign transitions to
each absorption.
Interpretation of Spectra – d3 and d8
ν1
ν1
The first peak is due to the 4A2g(F) 4T2g(F) transition and
has an energy equal to ∆o.
ν2
ν2
The second peak is due to the 4A2g(F) 4T1g(F) transition.
5
4/8/2012
Interpretation of Spectra –
d3
and
Interpretation of Spectra – d5
(high spin)
d8
ν3
ν1
ν2
ν3
Mn2+ compounds are white
to pale pink in color.
The third peak is due to the 4A2g(F) 4T1g(P) transition.
There are no spin allowed transitions for d5 high spin configurations.
Extinction coefficients are very low, though the selection rule is
relaxed by spin-orbit coupling.
References
Jahn-Teller Distortion
Racah, Giulio (1942). "Theory of complex spectra II". Physical Review 62: 438–462.
Tanabe, Yukito; Sugano, Satoru (1954). "On the absorption spectra of complex ions I". Journal
of the Physical Society of Japan 9 (5): 753–766.
3. Tanabe, Yukito; Sugano, Satoru (1954). "On the absorption spectra of complex ions II". Journal
of the Physical Society of Japan 9 (5): 766–779.
4. Tanabe, Yukito; Sugano, Satoru (1956). "On the absorption spectra of complex ions III". Journal
of the Physical Society of Japan 11 (8): 864–877.
5. Atkins, Peter; Overton, Tina; Rourke, Jonathan; Weller, Mark; Armstrong, Fraser; Salvador, Paul;
Hagerman, Michael; Spiro, Thomas et al (2006). Shriver & Atkins Inorganic Chemistry (4th ed.).
New York: W.H. Freeman and Company. pp. 478–483.
6. Douglas, Bodie; McDaniel, Darl; Alexander, John (1994). Concepts and Models of Inorganic
Chemistry (3rd ed.). New York: John Wiley & Sons. pp. 442–458.
7. Cotton, F. Albert; Wilkinson, Geoffrey; Gaus, Paul L. (1995). Basic Inorganic Chemistry (3rd d.).
New York: John Wiley & Sons. pp. 530–537.
8. Bertolucci, Daniel C. (1978). Symmetry and Spectroscopy: An Introduction to Vibrational and
Electronic Spectroscopy. New York: Dover Publications, Inc.. pp. 403–409, 539.
9. Lancashire, Robert John (4–10 June 1999), "Interpretation of the spectra of first-row transition
metal complexes", CONFCHEM, ACS Division of Chemical Education
10. Lancashire, Robert John (25 September 2006). "Tanabe-Sugano diagrams via spreadsheets".
Retrieved 29 November 2009.
11. Jørgensen, Chr Klixbüll (1954). "Studies of absorption spectra IV: Some new transition group
bands of low intensity". Acta Chem. Scand. 8 (9): 1502–1512.
12. Jørgensen, Chr Klixbüll (1954). "Studies of absorption spectra III: Absoprtion Bands as Gaussian
Error Curves". Acta Chem. Scand. 8 (9): 1495–1501.
1.
2.
Long axial
Cu-O bonds
= 2.45 Å
four short
in-plane
Cu-O bonds
= 2.00 Å
[Cu(H2O)6]2+
6
4/8/2012
The Jahn-Teller Theorem
Structural effects of Jahn-Teller distortion
The Jahn-Teller (J-T) theorem states that in molecules/ ions that have a degenerate
ground-state, the molecule/ion will distort to remove the degeneracy. This is a
fancy way of saying that when orbitals in the same level are occupied by different
numbers of electrons, this will lead to distortion of the molecule. For us, what is
important is that if the two orbitals of the eg level have different numbers of
electrons, this will lead to J-T distortion. Cu(II) with its d9 configuration is
degenerate and has J-T distortion:
High-spin Ni(II) – only one way
of filling the eg level – not
degenerate, no J-T distortion
All six Ni-O bonds
equal at 2.05 Å
two long axial
Cu-O bonds
= 2.45 Å
Cu(II) – two ways of filling eg level – it is
degenerate, and has J-T distortion
d9
d8
energy
Ni(II)
eg
t2g
eg
eg
t2g
t2g
Splitting of the d-subshell
by Jahn-Teller distortion
The CF view of the splitting of the d-orbitals is that those aligned with the
two more distant donor atoms along the z-coordinate experience less
repulsion and so drop in energy (dxz, dyz, and dz2), while those closer to the
in-plane donor atoms (dxy, dx2-y2) rise in energy.
An MO view
dx2-y2
of the splitting is that
the dx2-y2 in
eg
particular overlaps
energy
more strongly with
dz2
the ligand donor
orbitals, and so is
dxy
raised in energy. Note
t2g
that all d-orbitals with
Cu(II) in regular octaa ‘z’ in the subscript
hedral environment
dxz dyz drop in energy.
four short
in-plane
Cu-O bonds
= 2.00 Å
[Cu(H2O)6]2+
J-T distortion lengthens axial Cu-O’s
[Ni(H2O)6]2+
no J-T distortion
Structural effects of Jahn-Teller distortion on
[Cu(en)2(H2O)2]2+
long axial Cu-O
bonds of 2.60 Å
water
N
N
Cu
N
Short
in-plane
Cu-N
bonds of
2.03 Å
N
ethylenediamine
CCD:AZAREY
Cu(II) after J-T distortion
7
4/8/2012
Thermodynamic effects of Jahn-Teller distortion:
Structural effects of Jahn-Teller distortion on [Cu(en)3]2+
log K1(en) as a function of no of d-electrons
Cu(II)
12
N
10
N
N
Cu
logK1(en).
Short in-plane
Cu-N bonds of
2.07 Å
N
N
doublehumped
curve
8
6
Zn2+
4
Ca2+
2
N
0
1
CCD:TEDZEI
LFSE
Mn2+
d2
d3
d4
d5
d6
d7
0 .4Δo .8 1.2 .6 0 .4 .8
d8
2
3
4
5
6
7
8
9
10 11
d-electrons configuration
Experimental Evidence of LFSE
d1
rising baseline
due to ionic
contraction
0
long axial Cu-N
bonds of 2.70 Å
do
Extra
stabilization
due to J-T
distortion
= CFSE
d-electron configurations that lead to Jahn-Teller distortion:
d9
1.2 .6
d10
energy
0
eg
eg
t2g
d4 high-spin
Cr(II)
Mn(III)
t2g
d7 low-spin
Co(II)
Ni(III)
eg
eg
t2g
t2g
d8 low-spin
Co(I), Ni(II), Pd(II)
Rh(I),Pt(II), Au(III)
d9
Cu(II)
Ag(II)
8
4/8/2012
The strength of the Jahn-Teller effect is tabulated below:
(w=weak, s=strong)
Σ eHigh
spin
Low
spin
1 2 3 4 5 6 7 8 9 10
* * * s
- w w * *
w w - w w -
s
-
s
Charge Transfer Spectra
*
-
*There is only 1 possible ground state configuration.
- No Jahn-Teller distortion is expected.
Yuniar Ponco Prananto
Many transition metal complexes exhibit strong chargetransfer absorptions in the UV or visible range. These are
much more intense than dd transitions, with extinction
coefficients ≥ 50,000 L/mol-cm (as compared to 20 L/molcm for dd transitions).
Examples of these intense absorptions can be seen
in the permanganate ion, MnO4-. They result from
electron transfer between the metal and the
ligands.
In charge transfer absorptions, electrons from molecular
orbitals that reside primarily on the ligands are promoted
to molecular orbitals that lie primarily on the metal. This
is known as a charge transfer to metal (CTTM) or ligand
to metal charge transfer (LMCT). The metal is reduced as
a result of the transfer.
9
4/8/2012
LMCT typically occurs in complexes with the metal in a fairly high
oxidation state. It is the cause of the intense color of complexes in
which the metal, at least formally, has no d electrons (CrO42-, MnO41-).
LMCT occurs in the permangate ion, MnO41-. Electrons from the filled
p orbitals on the oxygens are promoted to empty orbitals on the
manganese. The result is the intense purple color of the complex.
MLCT typically occurs in complexes with π acceptor ligands. The empty π*
orbitals on the ligands accept electrons from the metal upon absorption of
light. The result is oxidation of the metal.
Examples of MLCT include iron(III) with acceptor ligands such as CN- or
SCN-. The complex absorbs light and oxidizes the iron(III) to iron(IV) state.
The metal may be in a low oxidation state (0) with carbon monoxide as the
ligand. Many of these complexes are brightly colored, and some appear to
exhibit both types of electron transfer.
Latihan Soal
3. Jelaskan 4 faktor yang mempengaruhi nilai 10Dq (Δo)!
1. Jelaskan apa yang dimaksud dengan: (a) prinsip
keelektronetralan Pauling; (b) CFSE; (c) deret
spektrokimia; (d) kompleks medan kuat dan medan
lemah; (e) Efek Jahn-Teller!
4. Gambarkan dua orbital molekul dari kompleks [NiCl4]2(Ar Ni = 28) ketika bersifat diamagnetik maupun
paramagnetik!
2. Jelaskan kelebihan dan kelemahan teori berikut
dalam menjelaskan sifat – sifat senyawa kompleks (a)
Teori ikatan valensi; (b) Teori medan kristal; (c) dan
Teori orbital molekul!
6. Mengapa pada kompleks Co(II) medan kuat cenderung
terjadi distorsi Jahn-Teller, sedangkan pada kompleks
Co(II) medan lemah tidak?
5. Jelaskan mengapa konfirgurasi elektron d1, d9, dan d10
tidak memiliki / memerlukan diagram Tanabe-Sugano!
10