Download geometry-unit-8-i-can-statements-trig

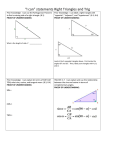
Geometry Unit #8 (right triangles, trig.)
1) G.SRT.8 I can use the Pythagorean Theorem to find
a missing side of a right triangle. (8.1)
PROOF OF UNDERSTANDING:
2) G.SRT.8 I can use the converse of the Pythagorean
Theorem to prove or disprove a triangle is a right
triangle. (8.1)
PROOF OF UNDERSTANDING:
What is the length of side c? _____________
Is the triangle above a right triangle? (Hint…change the
radical into decimal form first to decide which side should
be the longest side.)
3) I can label a right triangle with “opposite”,
“adjacent”, and “hypotenuse”. (8.3, 8.4)
PROOF OF UNDERSTANDING:
4) I can explain (in terms of SOH CAH TOA) what sine,
cosine, and tangent mean. (8.3, 8.4)
PROOF OF UNDERSTANDING:
SIN =
COS =
TAN =
Look at the 2 example triangles above. First locate the
angles 60° and 35°. Then, label your triangles with H, O,
and A.
Geometry Unit #8 (right triangles, trig.)
5) G.SRT.8 I can use a trig ratio for sine, cosine or
tangent to find the distance of a missing right triangle
side. (8.3, 8.4)
PROOF OF UNDERSTANDING:
6) G.SRT.8 I can use a trig ratio to find a missing angle
measurement. sin(¯¹), cos (¯¹), tan (¯¹) (8.3, 8.4)
PROOF OF UNDERSTANDING:
θ° = ?
X=?
θ
7) G.SRT.10 I can find the missing side of a triangle
when given SAS measures using the Law of Cosines.
(p565) PROOF OF UNDERSTANDING:
8) G. SRT.6, G.SRT.10 I can use the Law of Sines to
solve for the missing side lengths or angles of a
triangle. (p565) PROOF OF UNDERSTANDING:
=?
=?
Geometry Unit #8 (right triangles, trig.)
9) G.SRT.7 I can explain and use the relationship
between the sine and cosine in terms of
complementary angles.
PROOF OF UNDERSTANDING:
10) I can explain the relationship between sin, cos,
and tan on a unit circle.
PROOF OF UNDERSTANDING:
Explanation: _____________________________________
Explanation: _____________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
________________________________________________
11) G.SRT.9 I can find the area of a triangle with sides
a and b and included angle C using the formula Area =
(1/2) (ab) sin C. (10.5)
PROOF OF UNDERSTANDING:
12) G.SRT.8 I can use angles of depression or
elevation to help solve trig story problems. (8.5)
PROOF OF UNDERSTANDING:
Find the area of the non-right triangle below:
If the distance from A to C is 200 m, and AC is parallel to
BD, what is the height of the flagpole?
Geometry Unit #8 (right triangles, trig.)
13) G.SRT.8 I can use Pythagorean Theorem or trig
ratios to find missing side lengths or angle measures
of a right triangle.
B
PROOF OF UNDERSTANDING:
14) G.SRT.8 I can graph a right triangle on the
coordinate plane and find all missing angle and side
measurements.
PROOF OF UNDERSTANDING:
The diagram shows equilateral
triangle ABC sharing a side with
square ACDE. The square has
side lengths of 4. What is BE?
Justify your answer.
Graph triangle M (0,0); N (0,3); O (5,0). Find all side
lengths and angle measures.
A
C
E
D
Length of side MO: __________
Length of side MN: __________
Length of side ON: ___________
15) I can correctly identify basic labels on a triangles –
A,B,C representing angles and a,b,c representing the
side opposite each angle.
PROOF OF UNDERSTANDING:
m<MNO: __________
m<NMO: __________
m<NOM: __________
16) I can find the area of a regular polygon. (10.3,
10.5) PROOF OF UNDERSTANDING:
Side a has a length of
__________
What is the area of the pentagon above?
Label angle A.
Label angle B.
Label side c.