* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 10. 4 Other Angle Relationships in Circles - Geometry 10-12
Technical drawing wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Rational trigonometry wikipedia , lookup
Multilateration wikipedia , lookup
Problem of Apollonius wikipedia , lookup
Euler angles wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
Area of a circle wikipedia , lookup
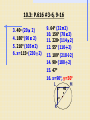
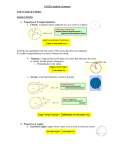
10.3: P.616 #3-6, 9-16 40o 3. (20× 2) 4. 180o (90× 2) 5. 210o (105×2) 6. x=115o (230÷2) 9. 64o (32×2) 10. 156o (78×2) 11. 228o (114×2) 12. 55o (110÷2) 13. 109o (218÷2) 14. 90o (180÷2) 15. 47o 16. x=90o, y=50o L M x° 40 ° y° K Inscribed Angles & Their Arcs: DO NOT COPY! A Inscribed Angle: an angle whose vertex is on a circle and whose sides contain the chords of a circle. (<CAD&<CBD) E Intercepted Arc: arc that lies in the interior of an inscribed angle If two inscribed angles of a circle intercept the same arc, then the angles are congruent. (m<AEB = mAB, measure of the central angle = measure of the intercepted arc) C D m<CAD = ½(CD) m<CBD = ½(CD) <CAD <CBD B 10.4: Secants, Tangents and Chords in Circles 5/6/2017 GOALS Use angles formed by tangents and chords to solve problems in geometry Use angles formed by lines that intersect a circle to solve problems There are 3 theorems you will use to solve for missing angles or arcs in a circle. You choose which theorem to use based on where 2 lines intersect. In other words, determine whether the intersection is: #1 On the circle: 1 chord and 1 tangent C B #2 Inside the circle: 2 chords A C C 4 D 3 A 1 1 2 2 The angle is half of its intercepted arc B D A m<1 or m<2 = (mAB + mCD) M<1 = mACB 2 secants or tangents B 2 1 #3 Outside the circle: m<3 or m<4 = (mBC + mAD) 2 The angles are the average of their intercepted arcs m<1 = (CD – AB) 2 The angle is half of the difference between the intercepted arcs Example #1: Tangent & Chord Line m is tangent to the circle. A) Solve for <VRT 1) m<VRT = V R m 102° m RST 2 2) m<VRT = (204°) 2 3) m<VRT = 102° •S T 204° Example #2: 2 Chords Solve for the value of x. S 40° 1) m<x ° = (mST + mRU) T 2 2) m<x° = (40° + 120°) 2 100° y° 3) m<x° = (160) = 80° X° 80° 2 U R 120° 4) m<y ° = 180° - 80° 5) m<y° = 100° Example #3: 1 secant & 1 tangent Solve for the value of x. 56° P x° 102° 50° S Solve for x: R 202° T 1) x = (mRTS - mPS) 2 2) x = (202° - 102°) 2 3) x = (100°) 2 4) x = 50° Example #4: 2 tangents Solve for the value of x. mRTS: 360°- 80°= 280° T 280° R 100° x° P 80° S 1) x° = (mRTS - mRS) 2 2) x° = ( 280° - 80°) 2 3) x° = (200°) 2 4) x° = 100° Assignment P.624 #2-4, 8, 9, 17, 18, 20-22 Draw circles… Show work… SUMMARY and ?’s Take a few minutes to write your summary. Make sure that you are writing 3 complete sentences. Also, don’t forget to come up with the questions for your notes as well… 10.4, P.624: # 2-4, 8, 9, 17, 18, 20-22 2. 210o (105×2) 3. 60o ((55+65)/2) 4. 65o ((190-60)/2) 8. 110o (220/2) 9. 280o (140×2) 17. 112.5o ((130+95)/2) 18. 50o ((25+75)/2) 20. 27o ((105-51)/2) 21. 26o ((122-70)/2) 22. 45o ((142-52)/2)