Download Easy Methods to Investigate Large Datasets Using

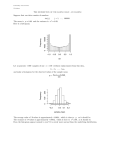
Easy Methods to Investigate Large Datasets Using ODS Graphics and New
Features in SAS® 9
Aimee Foreman, Ovation Research Group, San Francisco, CA
Miriam Cisternas, Ovation Research Group, Carlsbad, CA
ABSTRACT
Data analysts who took even a couple of applied statistics courses in school were probably taught that a thorough analysis
begins with a graphical examination of the data. And many of us even looked at univariate and bivariate scatter plots and
histograms as a precursor to our multivariable regression model-building assignments. But as we entered the professional
world, the size of our data sets increased, while our available time decreased. The practice of producing a graphical display of
data prior to analysis often went by the wayside in an effort to get the job done. Luckily, the availability of faster computers and
new graphical features in SAS 9 (including ODS Graphics) has allowed us to easily produce graphs to aid our understanding of
univariate, bivariate, and even multivariate relationships before commencing hypothesis testing or model-building analyses.
This paper provides the reader examples of code and the resulting graphical displays to support your understanding of your
data. This code can be easily adapted to your own projects.
INTRODUCTION
This paper is targeted toward SAS programmers with a working knowledge of BASE SAS. There are two data sources for the
included examples. The first is the 2003 Medical Expenditure Panel Survey (MEPS), a nationally representative survey on the
financing and utilization of medical care in the U.S., cosponsored by the Agency for Healthcare Research and Quality (AHRQ)
and the National Center for Health Statistics (NCHS). Specifically, the Household Component was used for the examples
below. These data are publicly available for download at http://www.meps.ahrq.gov. The second data source is the 19992000 National Health and Nutrition Examination Survey (NHANES), a series of studies on the health and nutrition of adults in
the United States administered by the National Center for Health Statistics (NCHS). Data that was used in the examples below
include the demographics, body measurements examination, blood pressure questionnaire, and blood pressure measurements
files. These data are also publicly available for download at http://www.cdc.gov/nchs/nhanes.htm. For simplicity, weights were
not used to generate the graphics for either data source, nor were the complex sampling designs taken into account.
UNIVARIATE GRAPHICS
When examining individual metric variables and their distributions, most analysts begin with a simple PROC MEANS to identify
the basic properties of the measure: minimum, quartiles, maximum, mean, and standard deviation (categorical variables are
usually examined through PROC FREQ output). But these measures do not always provide us with a picture of the shape of
the variable’s distribution. We can certainly grasp if the distribution is skewed, but how much does it appear to depart from
normality, and if so, how?
HISTOGRAM
One of the clearest and easiest ways of graphically displaying an individual variable is to create a histogram. As you no doubt
learned in your statistics classes, the histogram illustrates features of a measure’s distribution, such as its skewness and other
deviations from a normal distribution, that are difficult to grasp based only on PROC MEANS. It can also be very useful for
grouping a continuous variable into categories based on the variable’s distribution.
You can easily create a histogram using the HISTOGRAM statement in the UNIVARIATE procedure, but there are several
ways to improve upon the default histogram produced by the procedure. First, SAS automatically groups variable values into
bins based on the total number of observations graphed. The size of these bins can affect the shape of the resulting
histogram. A way to overcome this arbitrariness is to superimpose a smoothed histogram on top of your default histogram,
which highlights the overall shape of the distribution. Smoothing can be accomplished by parametric density estimation, but
since your raw variables typically may not fit a parametric fitted distribution, the safest bet is to use a nonparametric density
estimation. This is done using the KERNEL option on the HISTOGRAM statement to compute kernel density estimates. The
type of kernel function used does not have a large impact on the smoothing, so a good default is the NORMAL option (Jacoby
1997, p. 23).
Another feature that may improve your histogram is the addition of a fitted normal density curve using the NORMAL option on
the HISTOGRAM statement. By default, SAS uses the sample mean and standard deviation of the variable to fit the curve.
This feature allows you to observe how well or poorly the normal distribution models your variable, a detail that will become
important should you decide to do any model-fitting with underlying assumptions of normality.
-1-
Finally, it may be helpful to view summary statistics on the page with the histogram. This can be created with the INSET
statement. A number of statistical measures can be displayed in the inset box under the histogram, including sample size,
minimum, maximum, mean, standard deviation, percentiles, and hypothesis test statistics. This box allows you to see the
basic statistics you would see using PROC MEANS with the added and significant benefit of viewing a graphical display of the
variable’s distribution.
PROBABILITY PLOT
Another useful tool for examining distributions or testing how well the normal distribution (or many other theoretical
distributions) models your data measurement is the probability plot. This can be requested in PROC UNIVARIATE with the
PROBPLOT statement. If you specify the mean and standard deviation for the normal probability plot, SAS will display a
distribution reference line with those parameters. A comparison of the quantile plot with the normal reference line can pin-point
where the variable’s distribution departs from normality (Jacoby 1997, pp. 34-35).
Like the histogram, the probability plot can be enhanced to display a number of other statistics using the INSET statement.
Particularly useful statistics to display below this plot include the major quantiles of the displayed variable: P5, P10, Q1, etc.
EXAMPLE 1: CREATING A HISTOGRAM AND PROBABILITY PLOT
Suppose you were interested in examining the variable for body mass index (BMI) for a study on obesity using MEPS data.
The following code would produce both the histogram with smoothed histogram and normal histogram overlaid, and the
probability plot. Options in parentheses following the KERNEL option control the kernel function as well as the color and type
of line used; options in parentheses following the NORMAL option also control the color and type of line used. The INSET
statement specifies which statistics should be included in the box for the plot created in the previous line of code; for example,
the first INSET statement describes the box displayed with the histogram. The location of the inset box is controlled by the
POSITION= option; here it appears at the bottom margin (BM) of the graph. The options MU=EST and SIGMA=EST that
follow the PROBPLOT statement tell SAS to use the sample mean and sample standard deviation to construct the normal line
for the probability plot. Note the ODS statement that appears before PROC UNIVARIATE; this prevents SAS from displaying
all of the default tables and limits your output just to the graphics you are interested in.
ods exclude Moments BasicMeasures TestsForLocation Quantiles MissingValues ExtremeObs
ParameterEstimates GoodnessOfFit FitQuantiles;
proc univariate data=mepsdat;
title1 'Histogram (w Normal Distribution & Density Plot) and Prob Plot';
title2 'Specific Statistics included in plot inset box';
histogram bmindx53f /
kernel (k=normal color=green w=3 l=1)
normal (color = red w=3 l=2);
inset nmiss="# missing" (5.0)
n="N" min="Min" mean="Mean" median="Median" mode="Mode" max="Max" (6.3)
normal kernel(type)/ position=bm;
probplot bmindx53f / normal(mu=est sigma=est w=3 );
symbol1 v=circle;
inset P1 P5 P10 Q1 median Q3 P90 P95 P99 (6.3)/ position=bm;
label bmindx53f = 'Adult BMI' ;
run;
The histogram that is output from the code above shows a fairly symmetrical distribution centered about the median of 26.5.
The smoothed histogram appears very similar to the normal curve that has been superimposed on top of the histogram. But
we also see that this variable has a maximum value of 208, suggesting the existence of outliers. The probability plot clearly
shows several outliers beyond 50 that would need to be investigated before this variable were used in any analysis. This sort
of information would be difficult to gather from a simple PROC MEANS.
-2-
-3-
BIVARIATE GRAPHICS
When it comes to examining relationships between two variables, it is even more challenging to identify patterns based only on
a tabular description of the data provided by PROC MEANS or PROC FREQ. SAS offers many options for visualizing
relationships between two quantitative variables, or for investigating by-group differences for a given quantitative variable. The
output it produces can often save precious trees by producing multiple graphics on one page.
HISTOGRAM AND PROBABILITY PLOT
The histogram and probability plots remain useful in the bivariate case because SAS allows for side-by-side histograms and
probability plots to be displayed. This is useful when you have a variable whose distribution may differ by group level; for
example, if you suspect that blood pressure differs by gender or if you wish to compare the distribution of missed work days
per month for individuals with or without chronic conditions. Its implementation is simple: insert a CLASS statement with the
grouping variable into PROC UNIVARIATE where the histogram or probability plot is created. All other features that were
discussed in the Univariate Graphics section above are still applicable for these side-by-side graphs; for example, you can still
overlay a smoothed histogram and have an inset displaying key statistics for the variables.
BOX PLOT
There are several uses for the box plot, but it becomes particularly helpful when you have a variable with multiple levels by
which you want to examine the distribution of a quantitative variable. PROC BOXPLOT creates box-and-whisker plots that
display the mean, quartiles, minimum and maximum values of a variable by group level. The upper end of the box gives the
75th percentile, the line within the box gives the median, the symbol within the box represents the mean, the lower end of the
box gives the 25th percentile, and the location of the upper and lower whiskers as well as outlier symbols can be controlled with
the BOXSTYLE= option. As was the case with the histogram and probability plot, a box can be inserted underneath the
graphics to display statistics. This inset box is extremely useful in that it can be displayed to line up with the appropriate box
plot by group; this is accomplished using the INSETGROUPS option.
MATRIX PLOT
The utility of a matrix plot is clear to anyone who has been asked to examine the bivariate relationship between two or more
pairs of quantitative variables. Using the CORR procedure, it is possible to display on one page a matrix of bivariate
scatterplots for your variables of interest. Simply turn on ODS graphics capability using the ODS GRAPHICS statement,
specify the option PLOTS=MATRIX in the PROC CORR statement, and then turn off ODS graphics.
EXAMPLE 2: CREATING SIDE-BY-SIDE HISTOGRAMS AND PROBABILITY PLOTS
The following example shows the difference in age distribution for individuals with and without hypertension. Note that the SAS
code is exactly the same as the code in Example 1 (aside from differences in variable names), with the only change being the
addition of the CLASS statement here.
ods exclude Moments BasicMeasures TestsForLocation Quantiles MissingValues ExtremeObs
ParameterEstimates GoodnessOfFit FitQuantiles;
proc univariate data=mepsdat;
title2 'Side-by-side Histograms (w Normal Distribution & Density Plot) and Prob Plots';
title3 'Specific Statistics included in plot inset box';
class hypert;
histogram age31xf /
normal (color = red w=3 l=2)
kernel (k=normal color=green w=3 l=1);
inset nmiss="# missing" (5.0)
n="N" min="Min" mean="Mean" median="Median" mode="Mode" max="Max" (6.3)
normal kernel(type);
probplot age31xf / normal(mu=est sigma=est w=3 );
symbol1 v=circle;
inset P1 P5 P10 Q1 median Q3 P90 P95 P99 (6.3);
label age31xf = "Age"
hypert = "Hypertension Flag";
format hypert hypert.;
run;
As shown in the output below, it is clear that hypertension does vary by age in the MEPS sample. Those with hypertension
tend to be much older than those without. In addition, the histogram for the no-hypertension group shows a slightly bi-modal
distribution, with peaks in childhood and around age 40. The high bars at ages 0 and 85 indicate that there may be truncated
values for this variable, which would be an important feature to investigate further.
-4-
-5-
EXAMPLE 3: CREATING BOX PLOTS
This example illustrates how you can use graphics to verify the hypotheses concerning relationships between variables. The
MEPS data set includes variables for age and attained level of education; obviously, the two should be correlated, especially
for children who cannot reach higher levels of education. The SAS code below produces box plots that show the distribution of
age by all levels of education. The style of the box plots below is specified as SCHEMATIC. This style forces the upper
whisker to be drawn above the 75th percentile at a distance of 1.5 x (Interquartile Range), and the lower whisker to be drawn
below the 25th percentile at the same distance. Outliers are displayed as circles due to the IDSYMBOL=CIRCLE option. The
colors of the text, axis, and boxes are controlled by CTEXT=, CAXIS=, and CBOXES=, respectively. The INSETGROUP
statement creates boxes below the plots that align nicely with each level of education. Note that the input data set must be
sorted by the grouping variable, which is done below.
proc sort data=mepsdat out=temp
by educyearf_levs;
run;
proc boxplot data=temp;
title1 'Box plot by categorical variable';
title2 'Specific Statistics included in plot inset box';
plot age31xf*educyearf_levs / boxstyle=schematic idsymbol=circle
ctext=black caxis=black cboxes=black boxwidth=10 ;
insetgroup n Q1 Q2 Q3 range /pos=axis;
format educyearf_levs educ_cats.;
run;
As you would expect, the resulting box plots show a strong correlation between age and education level, with most children
clustered at the lowest education level and the highest number of respondents (n=9129) having completed at least one year of
college. It is interesting to notice that there are many outliers in the “Up to kdg” category where respondents are more
advanced in age. Another notable feature is that the respondents with a high school education are similar in age to those with
at least one year of college.
-6-
EXAMPLE 4: CREATING MATRIX PLOTS FOR MULTIPLE VARIABLES
This example produces a symmetric matrix plot of four quantitative variables included in NHANES: age(RIDAGEYR),
BMI(BMXBMI), diastolic blood pressure(BPXDAR), and systolic blood pressure(BPXSAR):
ods select SymMatrixPlot;
ods graphics on;
proc corr data=nhanesdat(keep=bpxsar bpxdar bmxbmi ridageyr) plots=matrix;
run;
ods graphics off;
The resulting scatterplots are easy to read and compact. The vertical and horizontal axes are identified by looking at the
variables on the diagonal. For example, the scatterplot in the upper right-hand-corner shows age on the vertical axis, and
diastolic blood pressure on the horizontal axis. Some interesting relationships emerge from this output: age and diastolic blood
pressure appear to be non-linearly related, as blood pressure seems to increase on average in middle age and decrease
slightly on average for the elderly. Diastolic and systolic blood pressure, on the other hand, look like they have a generally
linear relationship, but there is a cluster of 0 values for diastolic blood pressure that need to be examined; these could be
nonresponders or people who were excluded from the blood pressure survey for some reason.
-7-
MULTIVARIATE GRAPHICS
Multivariate relationships between variables can be difficult to visualize given the two-dimensionality of the screen or piece of
paper on which they are viewed. However, multivariate patterns are important to understand when you have many variables of
interest. They are easiest to examine when they involve one or more categorical variables by which you wish to group other
variables. For example, you may wish to examine whether females with heart disease have higher medical expenditures than
males with heart disease. The following techniques can help you investigate such a query.
HISTOGRAMS/PROBABILITY PLOT MATRIX
As was the case for bivariate data, multivariate distributions can be displayed by creating side-by-side plots in PROC
UNIVARIATE. Whereas the bivariate example included one CLASS variable, it is also possible to include two variables in the
CLASS statement. You can control how the matrix is displayed: if you have one categorical variable with 2 levels and the other
with 3 levels, you could tell SAS to display a 2x3 matrix. If you choose to create an inset box with statistics, there will be one
box produced with each histogram or probability plot. As a note of caution, this matrix is helpful for grouping variables with a
few levels, but the plots may become too small to be visually helpful when the class variables have too many categories.
SCATTERPLOT WITH PLOTTING SYMBOLS
The traditional scatterplot of two quantitative variables can be enhanced by inserting a grouping variable for comparison.
Instead of creating two separate scatterplots and lining them up side by side, it is possible to use just one scatterplot with
plotting symbols that differentiate between groups of observations. In this case the scatterplot still displays a quantitative
variable on the vertical axis and another on the horizontal axis, but the categorical variable is represented by different symbols,
colors, or shading for each data point. Additional introductory information on PROC GPLOT may be found in Cisternas 2005.
EXAMPLE 5: CREATING A MATRIX OF HISTOGRAMS
It is generally accepted that height varies by gender, but what if you wanted to know whether there was a combined
gender/ethnicity effect for height? A first step would include the creation of a matrix of histograms as shown below. Data used
are from NHANES. The NCOLS= and NROWS= options for the histogram tell SAS what dimensions to give the matrix.
ods exclude Moments BasicMeasures TestsForLocation Quantiles MissingValues ExtremeObs
ParameterEstimates GoodnessOfFit FitQuantiles;
proc univariate data=nhanesdat(keep=riagendr bmxht ridreth1);
-8-
title1 'Histograms matrix for 2 categorical variables (w Normal Distribution & Density
Plot) and Prob Plots';
title2 'Specific Statistics included in plot inset box';
class riagendr ridreth1;
histogram bmxht / normal (color = red w=3 l=2)
kernel (k=normal color=green w=3 l=1)
ncols = 4 nrows = 2;
inset nmiss="# missing" (5.0)
n="N" min="Min" mean="Mean" median="Median" mode="Mode" max="Max" (6.3)
normal kernel(type);
label bmxht = 'height'
riagendr = 'gender';
format riagendr gender. ridreth1 ethnicity4_.;
run;
In the resulting graphs, we can clearly see that Non-Hispanic Black and Other males are shorter on average than other males,
but this trend is not as pronounced for females. There also appear to be fewer shorter whites than Hispanics, Non-Hispanic
Blacks, or Others, but we could be seeing that there are more children of those ethnicities in this data set. This would be an
excellent opportunity to create bivariate histograms of age by ethnicity!
CONCLUSIONS
Graphics are under-utilized at the early stage of analysis because most SAS users are comfortable with and accustomed to the
traditional forms of tabular data examination. The examples included in this paper show that there is an added level of
understanding that can be gained by looking at your variables graphically. Whether you are working with a new data set with
which you are not yet familiar, or you are running a new analysis on a tried-and-true source, these graphics will help you make
more informed decisions about which outcomes you want to investigate, which covariates should be included in a model, or
what form you want your variables to take. SAS/GRAPH and ODS graphics are improving constantly, and the examples given
here are only a sample of the possibilities that exist.
-9-
REFERENCES
Cisternas, M.G., and Carpenter, A. 2005. “Extreme Graphics Make Over: Using SAS/GRAPH® to get the graphical output you
need.” Proceedings of the Thirtieth Annual SAS® Users Group International (SUGI) Conference, Philadelphia, Pennsylvania,
212-30.
Jacoby, William G. 1997. Statistical Graphics for Univariate and Bivariate Data. Thousand Oaks, CA: Sage Publications.
Jacoby, William G. 1998. Statistical Graphics for Visualizing Multivariate Data. Thousand Oaks, CA: Sage Publications.
Pasta, D.P. 2006. “Using Statistical Graphics to Understand Your Data (Not Just to Present Results.” Proceedings of the
Thirty-First Annual SAS® Users Group International (SUGI) Conference, San Francisco, CA.
CONTACT INFORMATION
Your comments and questions are valued and encouraged. Contact the authors at:
Aimee Foreman
Senior Statistical Analyst
Ovation Research Group
188 Embarcadero, Suite 200
San Francisco, CA 94105
[email protected]
Miriam Cisternas
Senior Research Scientist
Ovation Research Group
5051 Millay Court
Carlsbad, CA 92008
(760) 804-1946
[email protected]
SAS and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in
the USA and other countries. ® indicates USA registration.
Other brand and product names are trademarks of their respective companies.
-10-