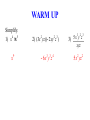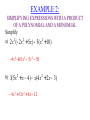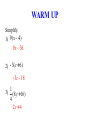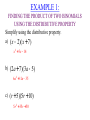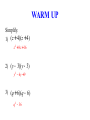* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Polynomial Packet Notes - Magoffin County Schools
Proofs of Fermat's little theorem wikipedia , lookup
Elementary mathematics wikipedia , lookup
Location arithmetic wikipedia , lookup
Horner's method wikipedia , lookup
Vincent's theorem wikipedia , lookup
System of polynomial equations wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Unit Essential Questions Are two algebraic expressions that appear to be different actually equivalent? What is the relationship between properties of real numbers and properties of polynomials? MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. MACC.912.A-SSE.A.1a: Interpret parts of an expression, such as terms, factors, and coefficients. WARM UP Simplify. 1) (3x + 2y) + 5x 8x + 2y 2) (4h + 5 j) - 3h h + 5j 3) (-6a + 5b) + 2a –4a + 5b KEY CONCEPTS AND VOCABULARY A monomial is a real number, a variable, or the product of real numbers and variables (Note: the variables must have positive integer exponents to be a monomial). The degree of a monomial is the sum of the exponents of its variables. A polynomial is a monomial or a sum of monomials. Standard form of a polynomial means that the degrees of its monomial terms are written in descending order. The degree of a polynomial is the same as the degree of the monomial with the greatest exponent. KEY CONCEPTS AND VOCABULARY 0 1 2 3 CLASSIFICATION OF POLYNOMIALS DEGREE NUMBER OF TERMS Constant 1 Monomial Linear 2 Binomial Quadratic 3 Trinomial Cubic 4 Polynomial with 4 terms EXAMPLES OF MONOMIALS EXAMPLES OF NOT MONOMIALS 6 x -3 p/7 4/y 4.75a2bc 3 g 9s 2t -5 8xy / z EXAMPLE 1: IDENTIFYING POLYNOMIALS Determine whether each expression is a polynomial. If it is a polynomial, classify the polynomial by the degree and number of terms. 2 3 a) 2x - 3x + 4x b) 12x 2 +10x -3 Polynomial, Cubic Trinomial c) x 2 + 3x + 4x 2 Polynomial, Quadratic Binomial Not a Polynomial d) 5 Polynomial, Constant Monomial EXAMPLE 2: WRITING POLYNOMIALS IN STANDARD FORM Write the polynomial in standard form. Then identify the leading coefficient. a) 4a2 - 7a + 3a5 3a5 + 4a2 - 7a Leading Coefficient = 3 b) 5h - 9 - 2h 4 - 6h 3 -2h 4 - 6h 3 + 5h - 9 Leading Coefficient = –2 c) -2 + 6t 2 - 7t + 2t 2 8t 2 - 7t - 2 Leading Coefficient = 8 EXAMPLE 3: ADDING POLYNOMIALS Simplify. 2 2 a) (2x - 7 + 5x) + (-4x + 6x + 3) -2x 2 +11x - 4 b) (5x + 7x 2 + 3) + (-5x 2 + x 3 - 4) x 3 + 2x 2 + 5x -1 EXAMPLE 4: SUBTRACTING POLYNOMIALS Simplify. a) (3x + 2 - x 2 ) - (4x - 5 + 2x 2 ) -3x 2 - x + 7 b) (12x 2 - 8x +11) - (-14 +10x 2 - 6x) 2x 2 - 2x + 25 EXAMPLE 5: SIMPLIFYING USING GEOMETRIC FORMULAS Express the perimeter as a polynomial. a) b) 3x 2 + 2x - 3 3x 2 - 4x +10 x2 - 4 x 2 - 7x + 2 5x 2 8x 2 -10x - 2 9x - 4x + 6 2 EXAMPLE 6: ADDING AND SUBTRACTING POLYNOMIALS IN REAL-WORLD APPLICATIONS The equations H = 3m +120 and C = 4m + 84 represent the number of Miami Heat hats, H, and the number of Cleveland Cavalier hats, C, sold in m months at a sports store. a) Write an equation for the total, T, of Heat and Cavalier hats sold. T = 7m + 204 b) Predict the number of Heat and Cavalier hats sold in 9 months. 267 Hats RATE YOUR UNDERSTANDING ADDING AND SUBTRACTING POLYNOMIALS MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. MACC.912.A-SSE.A.1a: Interpret parts of an expression, such as terms, factors, and coefficients. RATING 4 TARGET 3 2 1 LEARNING SCALE I am able to • add and subtract polynomials in real-world applications or in more challenging problems that I have never previously attempted I am able to • identify a polynomial and write polynomials in standard form • add and subtract polynomials I am able to • identify a polynomial and write polynomials in standard form with help • add and subtract polynomials with help I am able to • identify the degree of a monomial MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. WARM UP Simplify. 1) x 4 × x 5 x9 2) (3x yz)(-2xy z ) 2 -6x 3 y 3z 4 2 3 3 2 3 5x y z 3) xyz 5x 2 yz 2 KEY CONCEPTS AND VOCABULARY You can use the Distribution Property to multiply a monomial by a polynomial. EXAMPLE 1: MULTIPLYING A POLYNOMIAL BY A MONOMIAL Simplify. a) 2x 2 (6x 2 - 2x + 5) b) -3x 2 (x 2 + 3x - 8) 12x 4 - 4x 3 +10x 2 -3x 4 - 9x 3 + 24x 2 EXAMPLE 2: SIMPLIFYING EXPRESSIONS WITH A PRODUCT OF A POLYNOMIAL AND A MONOMIAL Simplify. a) 2x 2 (-2x 2 + 5x) - 5(x 2 +10) -4x 4 +10x 3 - 5x 2 - 50 b) 3(5x 2 + x - 4) - x(4x 2 + 2x - 3) -4x 3 +13x 2 + 6x -12 EXAMPLE 3: SIMPLIFYING USING GEOMETRIC FORMULAS Express the area as a polynomial. a) b) 7x 4x x 2 + 7x -12 x2 + 3 2x 3 + 6x 7x 3 + 49x 2 - 84x EXAMPLE 4: SOLVING EQUATIONS WITH POLYNOMIALS ON EACH SIDE Solve. a) 2x(x + 4) + 7 = (x + 9) + x(2x +1) +12 7 x= 3 b) x(x 2 + 3x + 5) + 2x 3 = 3x(x 2 + x + 5) +10 x = –1 RATE YOUR UNDERSTANDING MULTIPLYING A POLYNOMIAL BY A MONOMIAL MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. RATING 4 TARGET 3 2 1 LEARNING SCALE I am able to • multiply a polynomial by a monomial in more challenging problems that I have never previously attempted (such as solving equations) I am able to • multiply a polynomial by a monomial I am able to • multiply a polynomial by a monomial with help I am able to • understand that the distributive property can be applied to polynomials MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. WARM UP Simplify. 1) 9(x - 4) 9x - 36 2) -3(c + 6) -3c -18 3) 1 (8y +16) 4 2y + 4 KEY CONCEPTS AND VOCABULARY METHODS FOR MULTIPLYING POLYNOMIALS DISTRIBUTIVE PROPERTY METHOD Example: (x + 4)(x - 3) (x + 4)(x - 3) x(x - 3) + 4(x - 3) x 2 - 3x + 4 x - 12 x 2 + x - 12 FOIL METHOD Example: (x + 4)(x - 3) EXAMPLE 1: FINDING THE PRODUCT OF TWO BINOMIALS USING THE DISTRIBUTIVE PROPERTY Simplify using the distributive property. a) (x - 2)(x + 7) x 2 + 5x -14 b) (2a + 7)(3a - 5) 6a2 +11a - 35 c) (r + 5)(5r +10) 5r 2 + 35r + 50 EXAMPLE 2: FINDING THE PRODUCT OF TWO BINOMIALS USING THE FOIL METHOD Simplify using the FOIL method. a) (x + 3)(x + 9) x 2 +12x + 27 b) (5w - 2)(w + 3) 5w2 +13w - 6 c) (4k -1)(3k - 7) 12k 2 - 31k + 7 EXAMPLE 3: FINDING THE PRODUCT OF A BINOMIAL AND TRINOMIAL Simplify using the distributive property. 2 a) (2x - 6)(3x + x -1) 6x 3 -16x 2 - 8x + 6 b) (m -1)(m 3 - 4m +12) m4 - m3 - 4m2 +16m -12 c) (b2 - 4b + 3)(b - 2) b 3 - 6b2 +11b - 6 EXAMPLE 4: SIMPLIFYING PRODUCTS Simplify. a) (x + 2)[(x 2 + 3x - 6) + (x 2 - 2x + 4)] 2x 3 + 5x 2 - 4 b) [(x + 3x - 7) - (x - 2x + 6)](x - 4) 2 5x 2 - 33x + 52 2 RATE YOUR UNDERSTANDING MULTIPLYING POLYNOMIALS MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. RATING 4 TARGET 3 2 1 LEARNING SCALE I am able to • multiply two binomials or a binomial by a trinomial in more challenging problems that I have never previously attempted I am able to • multiply two binomials or a binomial by a trinomial I am able to • multiply two binomials or a binomial by a trinomial with help I am able to • understand the distributive property MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. WARM UP Simplify. 1) (z + 4)(z + 4) z 2 + 8z +16 2) (y - 3)(y - 3) y2 - 6y + 9 3) (q + 6)(q - 6) q 2 - 36 KEY CONCEPTS AND VOCABULARY MULTIPLYING SPECIAL CASES THE SQUARE OF A BINOMIAL THE PRODUCT OF A SUM AND DIFFERENCE (a + b)2 = (a + b)(a + b) = a2 + 2ab + b2 (a + b)(a – b) = a2 – b2 Or (a – b)2 = (a – b)(a – b) = a2 – 2ab + b2 EXAMPLE 1: SIMPLIFYING THE SQUARE OF A BINOMIAL (SUM) Simplify. 2 a) (x + 2) x 2 + 4x + 4 b) (5x + 2) 2 25x 2 + 20x + 4 c) (x + 5) 2 2 x 4 +10x 2 + 25 EXAMPLE 2: SIMPLIFYING THE SQUARE OF A BINOMIAL (DIFFERENCE) Simplify. a) (x - 7)2 x 2 -14x + 49 b) (2x -1)2 4x 2 - 4x +1 c) (x 2 - 3)2 x 4 - 6x 2 + 9 EXAMPLE 3: SIMPLIFYING THE PRODUCT OF A SUM AND DIFFERENCE Simplify. a) (x + 3)(x - 3) b) (2x + 5)(2x - 5) x2 - 9 4x 2 - 25 c) (x - 4)(4 + x) d) (x 2 + 6)(x 2 - 6) x 2 -16 x 4 - 36 EXAMPLE 4: SIMPLIFYING MORE CHALLENGING PROBLEMS WITH SPECIAL CASES Simplify. a) (x + 2y)2 x 2 + 4xy + 4y2 æ1 ö c) çè x + 2 ÷ø 4 b) (a - 6b)(a + 6b) a2 - 36b2 2 1 2 x +x+4 16 d) (x + 2)(x - 5)(x - 2)(x + 5) x 4 - 29x 2 +100 EXAMPLE 4: SIMPLIFYING MORE CHALLENGING PROBLEMS WITH SPECIAL CASES Simplify. e) (2x + 3)(2x - 3)(x +1) 4x 3 + 4x 2 - 9x - 9 f) [(4x +1)(4x -1)] + [(x + 5)2 ] 17x 2 +10x + 24 RATE YOUR UNDERSTANDING SPECIAL PRODUCTS MACC.912.A-APR.A.1: Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials. RATING 4 TARGET 3 2 1 LEARNING SCALE I am able to • simplify special products in more challenging problems that I have never previously attempted I am able to • find the square of a binomial • find the product of a sum and difference I am able to • find the square of a binomial with help • find the product of a sum and difference with help I am able to • understand that there are special rules to simplify the square of a binomial and the product of a sum and difference