Download Multiple Regression

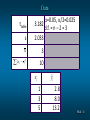
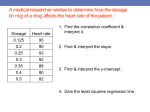
Simple Linear Regression
Estimation and Residuals
Chapter 14
BA 303 – Spring 2011
Slide 1
Point Estimation
ŷ  b0  b1 x
If 3 TV ads are run prior to a sale, we expect the mean
number of cars sold to be:
^
y = 10 + 5(3) = 25 cars
Slide 2
Confidence Interval of E(yp)

Confidence Interval Estimate of E(yp)
y p  t  /2 s y p
where:
confidence coefficient is 1 -  and
t/2 is based on a t distribution
with n - 2 degrees of freedom
The CI is an interval estimate of the mean
value of y for a given value of x.
Slide 3
Confidence Interval for E(yp)

Estimate of the Standard Deviation of yˆ p
(xp  x )
1
syˆ p  s

n  ( x i  x )2
2
(3  2)2
1
syˆ p  2.16025

5 (1  2)2  (3  2)2  (2  2)2  (1  2)2  (3  2)2
1 1
syˆ p  2.16025
  1.4491
5 4
Slide 4
Confidence Interval for E(yp)
The 95% confidence interval estimate of the mean
number of cars sold when 3 TV ads are run is:
y p  t /2 s y p
25 + 3.182(1.4491)
25 - 4.61
25 + 4.61
20.39 to 29.61 cars
Slide 5
Prediction Interval

Prediction Interval Estimate of yp
y p  t /2 sind
where:
confidence coefficient is 1 -  and
t/2 is based on a t distribution
with n - 2 degrees of freedom
The PI is an interval estimate of an individual
value of y for a given value of x. The margin
of error is larger than for a CI.
Slide 6
Prediction Interval for yp

Estimate of the Standard Deviation of an Individual
Value of yp
(xp  x )
1
 s 1 
2
n  ( xi  x )
2
sind
1 1
syˆ p  2.16025 1  
5 4
syˆ p  2.16025(1.20416)  2.6013
Slide 7
Prediction Interval for yp
The 95% prediction interval estimate of the number
of cars sold in one particular week when 3 TV ads
are run is:
y p  t /2 sind
25 + 3.1824(2.6013)
25 - 8.28
25 + 8.28
16.72 to 33.28 cars
Slide 8
Comparison
Point Estimate:
25
Confidence Interval:
20.39 to 29.61 cars
Prediction Interval:
16.72 to 33.28 cars
Slide 9
PRACTICE
PREDICTION INTERVALS AND
CONFIDENCE INTERVALS
Slide 10
Data
ttable
s
(x
i
=0.05, /2=0.025
3.182
d.f. = n – 2 = 3
2.033
x
3
 x )2
10
ŷi
xi
1
3
5
2.8
8.0
13.2
Slide 11
RESIDUAL ANALYSIS
Slide 14
Residual Analysis
 If the assumptions about the error term e appear
questionable, the hypothesis tests about the
significance of the regression relationship and the
interval estimation results may not be valid.
 The residuals provide the best information about e .
 Residual for Observation i
y i  yˆ i
 Much of the residual analysis is based on an
examination of graphical plots.
Slide 15
Residual Plot Against x

If the assumption that the variance of e is the same
for all values of x is valid, and the assumed
regression model is an adequate representation of the
relationship between the variables, then
The residual plot should give an overall
impression of a horizontal band of points
Slide 16
Residual Plot Against x
Residual
y  yˆ
Good Pattern
0
x
Slide 17
Residual Plot Against x
Residual
y  yˆ
Nonconstant Variance
0
x
Slide 18
Residual Plot Against x
Residual
y  yˆ
Model Form Not Adequate
0
x
Slide 19
xiyi
Residuals
xi
1
3
2
1
3
yi
ŷi
14
24
18
17
27
15
25
20
15
25
( yi  yˆ i )
-1
-1
-2
2
2
Slide 20
Residual Plot Against x
3
2
1
0
0
1
1
2
2
3
3
4
-1
-2
-3
Slide 21
Standardized Residuals

Standardized Residual for Observation i
y i  yˆ i
syi yˆ i
where:
syi yˆ i  s 1  hi
( x i  x )2
1
hi  
n  ( x i  x )2
Slide 22
Standardized Residuals
x=2
( xi  x ) 2
xi
1
3
2
1
3
1
1
0
1
1
4
s=2.1602
( xi  x ) 2
2
(
x

x
)
 i
0.2500
0.2500
0.0000
0.2500
0.2500
hi
0.4500
0.4500
0.2000
0.4500
0.4500
s yi  yˆi
1.6020
1.6020
1.9321
1.6020
1.6020
Slide 23
Standardized Residuals
xi yi
ŷi s yi  yˆi
1
3
2
1
3
15
25
20
15
25
14
24
18
17
27
( yi  yˆ i )
s yi  yˆ i
1.6020 -0.6242
1.6020 -0.6242
1.9321 -1.0351
1.6020 1.2484
1.6020 1.2484
Slide 24
Standardized Residual Plot


The standardized residual plot can provide insight
about the assumption that the error term e has a
normal distribution.
If this assumption is satisfied, the distribution of the
standardized residuals should appear to come from a
standard normal probability distribution.
Slide 25
Standardized Residual Plot
1.5000
1.0000
0.5000
0.0000
0
1
1
2
2
3
3
4
-0.5000
-1.0000
-1.5000
Slide 26
Standardized Residual Plot

All of the standardized residuals are between –1.5
and +1.5 indicating that there is no reason to question
the assumption that e has a normal distribution.
Slide 27
Outliers and Influential Observations
Detecting Outliers
• An outlier is an observation that is unusual in
comparison with the other data.
• Minitab classifies an observation as an outlier if its
standardized residual value is < -2 or > +2.
• This standardized residual rule sometimes fails to
identify an unusually large observation as being
an outlier.
• This rule’s shortcoming can be circumvented by
using studentized deleted residuals.
• The |i th studentized deleted residual| will be
larger than the |i th standardized residual|.
Slide 28
PRACTICE
STANDARDIZED RESIDUALS
Slide 29
Standardized Residuals
x
( xi  x ) 2
xi
3
( xi  x ) 2
2
 ( xi  x )
hi
s yi  yˆi
1
s
2.0330
2
(
x

x
)
 i
10
2
3
4
5
Slide 30
COMPUTER SOLUTIONS
Slide 32
Computer Solution
 Performing the regression analysis computations
without the help of a computer can be quite time
consuming.
Slide 33
Our Solution – Calculations
Slide 34
Our Solution – Calculations
Slide 35
Basic MiniTab Output
Slide 36
MiniTab Residuals, Prediction Intervals, and
Confidence Intervals
Slide 37
Excel Output
Slide 38
Slide 39