Download recursive functions

NCCU
Programming Languages
程式語言原理
Spring 2006
Lecture 7: Lisp,
Functional Programming in Scheme
1
Outline
• McCarthy’s Original Paper of Lisp:
– Recursive Functions of Symbolic
Expressions and Their computation by
Machine, Part 1,” 1960
課程網站 資源區下載閱讀
(Part 2 was never published)
• Functional Programming in Scheme, I
– eBook，課程網站 軟體區
2
Recursive Functions of Symbolic
Expressions and Their Application,
Part I
J OHN M C C ARTHY
Review: Amit Kirschenbaum
Seminar in Programming Languages
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 1/43
Historical Background
LISP ( LISt Processor ) is the second oldest
programming language and is still in widespread use
today.
Defined by John McCarthy from M.I.T.
Development began in the 1950s at IBM as FLPL Fortran List Processing Language.
Implementation developped for the IBM 704 computer
by the A.I. group at M.I.T.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 2/43
Historical Backgroung (Cont’d)
“ The main requirement was a programming system for
manipulating expressions representing formalized
declerative and imperative sentences so that the Advice
Taker could make deductions.”
Many dialects have been developed from LISP: Franz Lisp,
MacLisp, ZetaLisp . . .
Two important dialects
Common Lisp - ANSI Standard
Scheme - A simple and clean dialect. Will be used in
our examples.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 3/43
Imperative Programming
Program relies on modfying a state, using a sequence
of commands.
State is mainly modified by assignment
Commands can be executed one after another by
writing them sequentially.
Commands can be executed conditinonally using if
and repeatedly using while
Program is a series of instructions on how to modify
the state.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 4/43
Imperative Prog. (Cont’d)
Execution of program can be considered, abstractly as:
s0 → s1 · · · → sn
Program starts at state s0 including inputs
Program passes through a finite sequence of state
changes,by the commands, to get from s0 to sn
Program finishes in sn containing the outputs.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 5/43
Functional Programming
A functional program is an expression, and executing a
program means evaluating the expression.
There is no state, meaning there are no variables.
No assignments, since there is nothing to assign to.
No sequencing.
No repetition but recursive functions instead.
Functions can be used more flexibly.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 6/43
Why use it?
At first glance, a language without variables,
assignments and sequencing seems very impractical
Imperative languages have been developed as an
abstraction of hardware from machine-code to
assembler to FORTRAN and so on.
Maybe a different approach is needed i.e, from human
side. Perhaps functional languages are more suitable
to people.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 7/43
Advantages of functional programming
Clearer sematics. Programs correspond more directly
to mathematical objects.
More freedom in implementation e.g, parallel programs
come for free.
The flexible use of functions we gain elegance and
better modularity of programs.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 8/43
Some Mathematical Concepts
Partial Function - function that is defined only of part of
its domain.
Propositonal Expressions and Predicates Expressions whose possible values are T (truth) and F
(false).
Conditional Expressions - Expressing the dependence
of quantties on propositional quantities. Have the form
(p1 → e1 , · · · , pn → en )
Equivalent to
“If p1 then e1 , else if p2 then e2 , · · · else if pn then en ”
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 9/43
Mathematical Concepts (Cont’d)
Conditional expression can define noncommutative
propositional connectives:
p ∧ q = (p → q, T → F )
p ∨ q = (p → T, T → q)
¬p = (p → F, T → T )
Recursive function definitions - Using conditional
expressions, we can define recursive functions
n! = (n = 0 → 1, T → n · (n − 1)!)
Functions are defined and used, using λ-notation.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 10/43
Brief intro to λ-calculus
A formal system designed to investigate
function definition
function application
recursion
Can be called the
smallest universal programming language.
It is universal in the sense that any computable
function can be expressed within this formalism.
Thus, it is equivalent in expressive power to Turing
machines.
λ-calculus was developed by Alonzo Church in the
1930s
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 11/43
λ-notation
Defining a function in mathematics means:
Giving it a name.
The value of the function is an expression in the formal
arguments of the function.
e.g., f (x) = x + 1
Using λ-notation we express it as a λ-expression
λx . (+ x 1)
It has no name.
prefix notation is used.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 12/43
λ-notation (Cont’d)
The function f may be applied to the argument 1 :
f (1)
Similarly, the λ-expression may be applied to the
argument 1
(λx . (+ x 1))1
Application here means
Subtitue 1 for x: (+ x 1) ⇒ (+ 1 1)
Evaluate the function body: make the addition
operation .
Return the result: 2
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 13/43
Syntax of λ-calculus
Pure λ-calculus contains just three kinds of expressions
variables (identifiers)
function applications
λ-abstractions (function defintions)
It is convinient to add
predefined constants (e.g., numbers) and operations
(e.g., arithmetic operators)
hexpi
::=
|
|
|
var
const
(hexpi hexpi)
(λ var . hexpi)
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 14/43
Function Application
Application is of the form (E1 E2 )
E1 is expected to be evaluated to a function.
The function may be either a predefined one or one
defined by a λ-abstraction.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 15/43
λ-abstractions
The expression
(λx . (∗ x 2))
is the function of x which multiplies x by 2
The part of the expression that occurs after λx is called
the body of the expression.
When application of λ-abstraction occurs, we return
the result of the body evaluation.
The body can be any λ-expression, therefore it may be
a λ-abstraction.
The parameter of λ-abstraction can be a function itself
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 16/43
λ-abstractions
In mathematics there are also functions which return
functions as values and have function arguments.
Usually they are called operators or f unctionals
For example: the differentiation operator
d 2
x = 2x
dx
.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 17/43
Constants
Pure λ-calculus doesn’t have any constants like
0, 1, 2, . . . or built in functions like +, −, ∗, . . ., since they
can be defined by λ-expressions.
For the purpose of this discussion we’ll assume we
have them.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 18/43
Naming Expressions
Expressions can be given names, for later reference:
square ≡ (λx . (∗ x x))
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 19/43
Free and bound variables
Consider the expression
(λx . (∗ x y))2
x is bound: it is just the formal parameter of the
function.
y is free: we have to know its value in advance.
A variable v is called bound in an expression E if there
is some use of v in E that is bound by a decleration λv
of v in E .
A variable v is called f ree in an expression E if there is
some use of v in E that is not bound by any decleration
λv of v in E .
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 20/43
Reduction rule
The main rule for simplifiying expressions in λ-calculus
is called β -reduction.
Applying a λ-abstraction to an argument is an instance
of its body in which f ree occurences of the formal
parameter are substituted by the argument.
parameter may occur multiple times in the body
(λx . (∗ x x))4 → (∗ 4 4) → 16
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 21/43
Reduction rule
Functions may be arguments
(λf .(f 3))(λx .(− x 1))
(λf .(f 3))(λx .(− x 1))
→ (λx .(− x 1))3
→ (− 3 1)
→2
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 22/43
Expressions for Recursive Functions
The λ-notation is inadequte for defining functions
recursively
the function
n! = (n = 0 → 1, T → n · (n − 1)!)
should be converted into
! = λ((n)(n = 0 → 1, T → n · (n − 1)!))
There is no clear reference from ‘!’ inside the λ-clause,
to the expression as a whole.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 23/43
Expressions for Recursive Functions
A new notation: label(a, E) denotes the expression E ,
provided that occurences of a within E are to be
referred as a whole.
For example, for the latter function the notation would
be
label(!, λ((n)(n = 0 → 1, T → n · (n − 1)!)
(There is a way to describe recursion in λ-calculus,
using Y-combinator, but McCarthy doesn’t use it.)
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 24/43
S-Expressions
A new class of Symbolic expressions.
S-Expression are composed of the special characters
( - start of composed expression
) - end of composed expression
• - composition
and “an infinite set of distinguishable atomic
symbols”.
e.g.,
A
ABA
APPLE-PIE-NUMBER-3
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 25/43
S-Expression : Definition
Atomic symbols are S-expression.
if e1 and e2 are S-expressions then so is (e1 · e2 )
examples
AB
(A· B)
((AB· C) · D)
S-expression is then simply an ordered pair.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 26/43
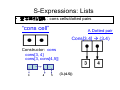
S-Expressions: Lists
• 基本資料結構：cons cells/dotted pairs
“cons cell”
A Dotted pair
Cons[3,4] Æ (3.4)
Constructor: cons
cons[3, 4]
cons[3, cons[4,5]]
3
4
5
(3.(4.5))
S-Expressions: Lists
•一般資料結構中的串列由許多cons cells組成，
最後的元素為empty list
•Empty list: null, nil, ‘()
The empty list
(a.k.a. null or nil)
cons[1, cons[3,cons[2, nil]]] =
(1.(3.(2.nil)))
1
3
2
S-Expression : Lists
The list
(m1 , m2 , . . . , mn )
is represented by the S-expression
(m1 · (m2 · (· · · (mn · N IL) · · · )))
N IL is an atomic symbol, used to terminate lists, also
known as the empty list.
(m) stands for (m · N IL)
(m1 , m2 , . . . , mn · x) stands for
(m1 · (m2 · (· · · (mn · x) · · · )))
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 27/43
M-expressions
Meta-expressions are functions of S-expressions, also
called S-functions.
Written in conventional functional notation.
There are some elementry S-functions and predicates
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 28/43
M-expressions
atom - atom[x] has the value T or F according to
whether x is atomic symbol.
atom[X] = T .
atom[(X·A)] = F .
eq - eq[x;y] is defined iff both x and y are symbols.
eq[x;y] = T if x and y are the same symbol and
eq[x;y] = F otherwise
eq[X;X] = T .
eq[X;A] = F .
eq[X;(A · B)] is undefined
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 29/43
M-expressions
car - car[x] is defined iff x is not atomic.
car[(e1 · e2 )]=e1
car[(X·A)] = X.
car[(X·A)· Y)]= (X·A).
cdr - cdr[x] is also defined iff x is not atomic.
cdr[(e1 · e2 )]=e2
cdr[(X·A)] = A.
cdr[(X·A)· Y)]= Y.
cons - cons[x;y] is defined for any x and y. It is the list
constructor
cons[(e1 ;e2 )]=(e1 · e2 )
cons[X;A] = (X·A).
cons[(X·A);Y]= ((X·A)· Y).
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 30/43
M-expressions
Compositions of car and cdr arise very frequently.
Many expressions can be written more concisely if we
abbreviate.
cadr[x] ≡ car[cdr[x]]
caddr[x] ≡ car[cdr[cdr[x]]]
cdadr[x] ≡ cdr[car[cdr[x]]]
expressions are not defined for every x. depends on
the list structure.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 31/43
Recursive S-functions
Forming new functions of S-expression by conditional
expression and recursive definition gives us much
larger class of functions.
In fact all computable functions.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 32/43
Recursive S-function examples
ff[x] - returns the first atomic symbol of the
S-expression x, ignoring the parentheses.
ff[x] = [atom[x]→x ; T → ff[car[x]]]
ff[(A·B)]
= [atom[(A·B)]→ (A·B) ; T → ff[car[(A·B)]]]
= [F →(A·B);T → ff[car[(A·B)]]]
= ff[car[(A·B)]]
= ff[A]
= ff[atom[A]→A ; T →ff[car[A]]]
= [T →A ; T →ff[car[A]]]
=A
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 33/43
Transform M-expressions to S-expressions
There is a transformation mechanism that translate an
M-expression E into S-expression E ∗
if E is an S-expression, E ∗ is (QUOTE E ).
M-expression f [e1 ; . . . ; en ] is translated to (f ∗ e∗1 . . . e∗n ).
Thus, {cons[A; B]}∗ is (CONS (QUOTE A) (QUOTE B))
{[p1 → e1 ]; . . . ; [pn → en ]}∗ is (COND (p∗1 e∗1 ) . . . (p∗n e∗n ))
{λ[x1 ; . . . ; xn ]E}∗ is (LAMBDA(x1 . . . xn ) E ∗ .
{label[a; E]}∗ is (LABEL a E ∗ )
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 34/43
What do we gain?
Unifying Symbol-level and Meta-level, gives us a way
to treat expressions over symbols exactly the same as
symbols.
Functions and data are the same.
Thus we can write a program, which write another
program and evaluating it.
This is useful in AI.
Furthermore, we can expand the language with new
features.
LISP interpreters are easily implemented in LISP.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 35/43
S-function apply
“Plays the theoretical role of a universal Turing
machine and the practical role of an interpreter”.
Formally,
If f is an S-expression for an S-function f 0
and args is a list of arguments of the form
(arg1 , . . . , argn ) where arg1 , . . . , argn are
S-expressions,
Then apply[f ; args] and f 0 [arg1 , . . . , argn ] are
defined for the same values of arg1 , . . . , argn and
are equal when defined.
example: λ[[x; y]; cons[car[x]; y]] [(A, B); (C, D)] ≡
apply[(LAMBDA, (X, Y )(CONS(CARX)Y ))((A B)(C D))] =
(A C D)
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 36/43
S-function eval
serves both as a formal definition of the language and
as an interpreter
Before apply applies the function f on the list of
arguments (arg1 , . . . , argn ), it sends them to eval for
evaluating the S-expressions which represents them.
> (eval ’(lambda (x) (+ x 1)))
#<procedure>
’(lambda (x) (+ x 1)))
is an S-expression which repersents a function. eval
evalutes it and return its value, which is indeed a function
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 37/43
Implementing eval
(define (eval exp env)
(cond ((self-evaluating? exp) exp)
((variable? exp) (lookup-variable-value exp env))
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp)
(make-procedure (lambda-parameters exp)
(lambda-body exp)
env))
((begin? exp)
(eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((application? exp)
(apply (eval (operator exp) env)
(list-of-values (operands exp) env)))
(else
(error "Unknown expression type -- EVAL" exp))))
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 38/43
Strength of the mechanism
Extending the language is done easily by adding
required forms to eval.
Just add syntax and evaluation rules.
Paraphrasing Oscar Wilde: LISP programmers know
the value of everything but the cost of nothing.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 39/43
The cost
Performance of LISP systems became a growing issue
Garbage Collection.
Representation of internal structures.
Became difficult to run on the memory-limited
hardware of that time.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 40/43
LISP Machines
The solution was LISP machine - a computer which
has been optimized to run LISP efficiently and provide
a good environment for programming in it.
Typical optimizations to LISP machines
Fast function calls.
Efficient representation of lists.
Hardware garbage collection.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 41/43
LISP in the real world
de-facto standard in AI
NLP
Modelling speech and vision
Some more
AutoCAD
Yahoo Store
Emacs
Mirai, the 3d animation package was used to create
Gollum in Lord Of The Rings.
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 42/43
The End
((lambda(x)(x x))
(lambda(x)(x x)))
Recursive Functions of Symbolic Expressions and Their Application, Part I – p. 43/43
Scheme
•
•
•
•
•
•
•
: an Interpreter for
Extended Lambda Calculus
Developed in 1975 by G. Sussman and G. Steele
A version of LISP
Simple syntax, small language
Closer to initial semantics of LISP
Provides basic list processing tools
Allows functions to be first-class values
Provides some support for lazy evaluation
3
The Structure of a Scheme Program
•
•
•
•
All programs and data are expressions (S-expr)
Expressions can be atoms or lists
Atom: number, string, identifier, character, boolean
List: sequence of expressions separated by spaces,
between parentheses
• Syntax:
expression → atom | list
atom
→ number | string | identifier | character | boolean
list
→ ( expr_seq )
expr_seq → expression expr_seq | expression
4
S-expressions
• In LISP/Scheme, data & programs are all of the same
form: S-expressions (Symbolic-expressions)
– an S-expression is either an atom or a list (ignore dotted
pairs)
Atoms
ƒ
ƒ
ƒ
ƒ
ƒ
numbers
characters
strings
Booleans
symbols
4
3.14
1/2
#xA2
#\a
#\Q
#\space
#\tab
"foo"
“Hello Hi"
#t
#f
Dave
num123
#b1001
"@%!?#"
miles->km
!_^_!
symbols are sequences of letters, digits, and "extended alphabetic characters"
+ - . * / < > = ! ? : $ % + & ~ ^
can't start with a digit, case insensitive
5
S-expressions (cont.)
• Lists
()
(L1 L2 . . . Ln)
is a list
is a list, where each Li is
either an atom or a list
for example:
• ()
• (a b c d)
• (((((a)))))
(a)
((a b) c (d e))
6
A List is a recursive structure!
• (cdr a-list) evaluates also to a list!
Data Definition of a list:
Self-referential data structure!
A list consists of:
1) The empty list, empty, or
2) (cons z loz) where z is a value and
loz is a list.
…
<x1>
first (car)
<x2>
<xn>
Rest (cdr) is also a list
7
List manipulation in Lisp & Scheme
• Three primitives and one constant
– get head of list: car
– get rest of list: cdr
– add an element to a list: cons
– null list: nil or ()
• Add equality ( = or eq?), conditional expression,
and recursion, and this is a universal model of
computation
• “quote” for distinguishing data from programs.
8
Interacting with Scheme: Evaluation
• Interpretor: "read-eval-print" loop
>1
1
Reads 1, evaluates it (1 evaluates to itself), then prints its value
> (+ 2 3)
5
+ => function + (or called procedure)
2 => 2
3 => 3
Applies function + on operands 2 and 3 => 5
9
Evaluation
• Constant atoms - evaluate to themselves
42
3.14
"hello"
#/a
#t
- a number
- another number
- a string
- character 'a'
- boolean value "true"
> "hello world"
"hello world"
10
Evaluation
• Identifiers (symbols) - evaluate to the value
bound to them
(define a 7)
>a
7
>+
#<procedure +>
11
Evaluation
• Lists - evaluate as "function calls":
(function arg1 arg2 arg3 ...)
• First element must evaluate to a function (procedure)
• Recursively evaluate each argument
• Apply the function on the evaluated arguments
> (- 7 1)
6
> (* (+ 2 3) (/ 6 2))
15
12
Operators - More Examples
• Prefix notation
• Any number of arguments
> (+)
0
> (+ 2 3 4)
9
> (+ 2)
2
> (- 10 7 2)
1
> (+ 2 3)
5
> (/ 20 5 2)
2
13
Preventing Evaluation (quote)
• Evaluate the following:
> (1 2 3)
Error: attempt to apply non-procedure 1.
• Use the quote to prevent evaluation:
> (quote (1 2 3))
(1 2 3)
• Short-hand notation for quote:
> '(1 2 3)
(1 2 3)
14
More Examples
(define a 7)
a
'a
=> 7
=> a
(+ 2 3)
'(+ 2 3)
((+ 2 3))
=> 5
=> (+ 2 3)
=> Error: attempt to apply non-procedure 5.
'(her 3 "sons")
=> (her 3 "sons")
• Make a list:
(list 'her (+ 2 1) "sons")
(list '(+ 2 1) (+ 2 1))
=>
=> (her 3 "sons")
((+ 2 1) 3)
15
Forcing Evaluation (eval)
(+ 1 2 3)
'(+ 1 2 3)
(eval '(+ 1 2 3))
=> 6
=> (+ 1 2 3)
=> 6
(list + 1 2)
(eval (list + 1 2))
=> (+ 1 2)
=> 3
• Eval evaluates its single argument
• Eval is implicitly called by the interpretor to evaluate
each expression entered:
“read-eval-print” loop
16
Special Forms
• Have different rules regarding whether/how arguments
are evaluated
(define a 5)
; binds a to 5, does not evaluate a
a
5
(quote (1 2 3))
; does not evaluate (1 2 3)
• There are a few other special forms – discussed later
17
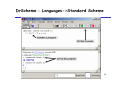
Using Scheme: DrScheme an IDE for Scheme
How to Design Programs
(methodology)
課程網站下載
Windows 版
Scheme
(language)
DrScheme
(environment)
18
Scheme Programming Environment
DrScheme
http://www.drscheme.org/
定義框
求值框
19
DrScheme : Languages->Standard Scheme
20
List Operations
• cons – returns a list built from head and tail
(cons 'a '(b c d))
(cons 'a '())
(cons '(a b) '(c d))
(cons 'a (cons 'b '()))
=> (a b c d)
=> (a)
=> ((a b) c d)
=> (a b)
(cons 'a 'b)
=> (a . b) ; dotted pair, improper list
21
List Operations
• car – returns first member of a list (head)
(car
(car
(car
(car
'(a b c d))
=> a
'(a))
=> a
(a b) =>
'((a b) c d))
'(this (is no) more difficult))
=> this
• cdr – returns the list without its first member (tail)
(cdr '(a b c d))
(cdr '(a b))
(cdr '(a))
(cdr '(a (b c)))
=>
=>
=>
=>
(b c d)
(b)
()
((b c))
(car (cdr (cdr '(a b c d))))
(caddr '(a b c d))
=> c
=> c
22
List Operations
• null? – returns #t if the list is null ()
#f otherwise
• list – returns a list built from its arguments
(list 'a 'b 'c)
(list 'a)
(list '(a b c))
(list '(a b) 'c)
(list '(a b) '(c
=>
=>
=>
=>
d))
(a b c)
(a)
((a b c))
((a b) c)
=> ((a b) (c d))
23
List Operations
• length – returns the length of a list
(length '(1 3 5 7))
(length '((a b) c))
2
=> 4
=>
• reverse – returns the list reversed
(reverse '(1 3 5 7))
(reverse '((a b) c))
=> (7 5 3 1)
=> (c (a b))
• append – returns the concatenation of the lists received
as arguments
(append '(1 3 5) '(7 9)) => (1 3 5 7 9)
(append '(a) '())
=> (a)
(append '(a b) '((c d) e)) => (a b (c d) e)
24
Type Predicates
• Check the type of the argument and return #t or #f
(boolean? x)
(char? x)
(string? x)
(symbol? x)
(number? x)
(list? x)
(procedure? x)
; is x a boolean?
; is x a char?
; is x a string?
; is x a symbol?
; is x a number?
; is x a list?
; is x a procedure (function)?
25
Boolean Expressions
(< 1 2)
(>= 3 4)
(= 4 4)
(eq? '(a b) '(a b))
(equal? '(a b) '(a b))
(not (> 5 6))
(and (< 3 4) (= 2 3))
(or (< 3 4) (= 2 3))
=> #t
=> #f
=> #t
=> #f
=> #t
; same object? By reference
; recursively equivalent
; structure? By value
=> #t
=> #f
=> #t
• and, or are special forms - evaluate arguments only while
needed (short-circuited operations)
– (or (> 2 1) (/ 5 0) => #t
26
Conditional Expressions
• if – has the form:
(if <test_exp> <then_exp> <else_exp>)
(if (< 5 6) 1 2) => 1
(if (< 4 3) 1 2) => 2
• Anything other than #f is treated as true:
(if 3 4 5)
(if '() 4 5)
=> 4
=> 4
; as opposed to Lisp!!
• if is a special form - evaluates its arguments only when
needed:
(if (= 3 4) 1 (2))
(if (= 3 3) 1 (2))
Error:
=> attempt to apply non-procedure
27
2. => 1
Conditional Expressions
• cond – has the form:
(cond
(<test_exp1> <exp1> ...)
(<test_exp2> <exp2> ...)
...
(else <exp> ...))
(define n -5)
(cond ((< n 0) "negative")
((> n 0) "positive")
(else "zero"))
=> "negative"
• cond is a special form - evaluates its arguments only
28
when needed
Syntax (C vs. Scheme)
C
Scheme
1+2+3
3+4*5
factorial (9)
(a == b) && (c != 0)
(low < x) && (x < high)
f (g(2,-1), 7)
(+ 1 2 3)
(+ 3 (* 4 5))
(factorial 9)
(and (= a b) (not (= c 0)))
(< low x high)
(f (g 2 -1) 7)
29
Functions
• Create a function by evaluating a lambda expression:
(lambda (id1 id2 ...) exp1 exp2 ...)
–
–
–
–
id1 id2 ...
- formal parameters
exp1 exp1 ...
- body of the function
return value of function
- last expression in body
return value of lambda expression - the (un-named) function
(lambda (x) (* x x))
=> #<procedure>
– Returns an un-named function that takes a parameter and
returns its square
30
Functions
• Call a function by applying the evaluated lambda
expression on its actual parameters:
((lambda (x) (* x x)) 3) => 9
the function
the actual parameter
• How can you reuse the function?
– You can’t!
• Why is it then useful?
– Return a function from another function
• What if you REALLY want to reuse it?
31
Functions
• Bind a name to a function:
(define square (lambda (x) (* x x)))
square
#<procedure>
• Equivalent short-hand notation (typical way to use it):
(define (square x) (* x x))
• Now call the function:
(square 3)
=> 9
32
Functions
• Functions vs. variables:
(define f 3)
f
(f)
(define (f) 3)
f
(f)
=> 3
=> Error: attempt to apply non-procedure
3.
=> #<procedure>
=> 3
• Last definition is equivalent to:
(define f (lambda () 3)); a function that takes no parameters and
; returns 3
33
Functions
C
Scheme
if (a == 0)
return f(x,y) ;
else
return g(x,y) ;
(if (= a 0)
(f x y)
(g x y))
34
Functions are First-Class Values
C
if (a == 0)
return f(x,y) ;
else
return g(x,y) ;
repeated arguments (x,y)
• Can we write it better in Scheme?
Scheme
((if (= a 0)
f
g)
x y)
evaluates to either #<procedure f> or
#<procedure g>
it is then applied on arguments x and
35 y
Recursion
• Recursion plays a greater role in Scheme than in other
languages
• Why?
• Functional programming – avoid side effects
(assignments) and iterations
• Recursive data structures – a list is either empty, or has
a car and a cdr; the cdr is (again) a list
• Elegance – recursive algorithms are considered more
elegant than iterative ones (just ask a Scheme or Lisp
programmer!)
36
Recursion
• How do you solve a problem recursively?
• Do not rush to implement it
• Think of a recursive way to describe the problem:
– Show how to solve the problem in the general case, by
decomposing it into similar, but smaller problems
– Show how to solve the smallest version of the problem (the base
case)
• Now the implementation should be straightforward (in
ANY language)
– But don't forget to handle base case first when implementing
37
Recursion
• How do you THINK recursively?
• Example: define factorial
factorial(n) = 1 * 2 * 3 * ...(n-1) * n
factorial (n-1)
1
if n=1
(the base case)
factorial(n) =
n * factorial(n-1) otherwise
(inductive step)
38
Recursion
• Implement factorial in Scheme:
(define (factorial n)
(if (= n 1)
1
(* n (factorial (- n 1)))))
(factorial 4) => 24
39
Recursion
• Fibonacci:
0
fib(n) =
if n = 0
1
if n = 1
fib(n-1) + fib(n-2) otherwise
• Implement in Scheme:
(define (fib n)
(cond
((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1)) (fib (- n 2))))))
40
Recursion
• Length of a list:
0
len(lst) =
if list is empty
1 + len ( lst-without-first-element ) otherwise
• Implement in Scheme:
(define (len lst)
(if (null? lst)
0
(+ 1 (len (cdr lst)))))
41
Recursion
• Sum of elements in a list of numbers:
0
if list is empty
first-element +
sum (lst-without-first-element)
otherwise
sum(lst) =
• Implement in Scheme:
(define (sum lst)
(if (null? lst)
0
(+ (car lst) (sum (cdr lst)))))
42
Recursion
• Check membership in a list:
(define (member? x lst)
(cond
((null? lst) #f)
((equal? x (car lst)) #t)
(else (member? x (cdr lst)))))
43
More recursive functions: append
¾ (define (append x y)
(cond ((null? x) y)
((null? y) x)
(else (cons (car x) (append (cdr x) y)))
)
cdr-recursion
)
(append ‘() ‘())
value: ()
(append ‘() ‘(1 2 3))
value: (1 2 3)
(append ‘(1 2) ‘(3 (4) 5) )
value: (1 2 3 (4) 5)
44
Reverse a List, version 1
¾ (define (reverse l)
(cond ((null? l) l)
(else (append (reverse (cdr l))
(list (car l)) )
)
cdr-recursion
)
)
¾ (reverse ‘(a b c d) )
value: (d c b a)
¾ (reverse ‘(a (2 b c) d))
value: (d (2 b c) a)
;; Not what we want
45
Atom Predicate
• Write a function that takes a parameter x and
returns #t if x is an atom, and false
otherwise. Using cond:
(define (atom? x)
(cond ((symbol? x) #t)
((number? x) #t)
((char? x) #t)
((string? x) #t)
((null? x) #t)
(else #f)
)
)
46
Reverse a List, version 2
(define (reverse l)
(cond ((null? l) l)
((atom? (car l))
(append (reverse (cdr l))
(list (car l))))
(else (append (reverse (cdr l))
(list (reverse (car l))))
car-cdr-recursion
)
))
¾ (reverse ‘(a b c d) )
value: (d c b a)
¾ (reverse ‘(a (2 b c) d))
value: (d (c b 2) a)
47
Recursion: Counting Atoms
• Count the number of atoms in a general list
• >(count-atoms ‘(1 2 3)) => 3
• >(count-atoms ‘(1 (2 3) (4 (5)))) => 5
• Implement in Scheme:
(define (count-atoms lst)
(cond ((null? lst) 0)
((atom? lst) 1)
(else (+ (count-atoms (car lst)) (count-atoms (cdr lst))))
))
car-cdr-recursion
48
Equality checking
The eq? function only works for atoms, not for lists
¾ (eq? ‘() ‘())
value: #t
¾ (eq? (cons 1 ‘()) (cons 1 ‘()) )
value: #f
Why?
• (cons 1 ‘()) produces a new list
• (cons 1 ‘()) produces another new list
• different structures in memory: (eq? (cons 'a '()) (cons 'a '()))
evaluates to #f.
• eq? checks if two arguments are the same object
• consider pointers or objects vs object references in Java
• atoms and symbols are stored uniquely
49
Scheme: Equality Test, Revisited
• the operators: =, eq?, eqv?, equal? ;
– ‘=‘ tests sameness of numbers ;
– eq? tests sameness of symbols ; note: each
application of cons constructs a new cell ;
• (eq? (cons 1 2) (cons 1 2)) returns #f! ;
– eqv? tests sameness of numbers, symbols and
booleans ; (as well as vectors, strings, and chars) ;
– equal? is a universal test for sameness ; (tests all
of the above and lists as well) ;
• note: (equal? (cons 1 2) (cons 1 2)) returns #t! ;
the difference is mainly one of efficiency ; use the
predicate designed for the task at hand
50
Logical Procedures
• “true” stands for #t; “false” stands for #f (‘())
• “not object” { “false” object” }
– These procedures return #t if object is false; otherwise they
return #f.
• “and object …”
– This procedure returns #t if none of its arguments are #f.
Otherwise it returns #f.
• “or object …”
– This procedure returns #f if all of its arguments are #f.
Otherwise it returns #t.
¾ The arguments of “or”, “and” are evaluated sequentially
¾ “or”: until a true value is found
¾ “and”: until a false value is found
51
Equality checking for lists
For lists, need a comparison function that does a
structural equality test:
¾ (define (equal? x y)
(or
(and (atom? x) (atom? y) (eq? x y) )
(and
(and (not (atom? x)) (not (atom? y)))
(equal? (car x) (car y))
(equal? (cdr x) (cdr y))
)
)
)
¾ The arguments of “or”, “and” are evaluated sequentially
¾ “or”: until a true value is found
¾ “and”: until a false value is found
52
Repetition via recursion
• pure LISP/Scheme does not have loops
– repetition is performed via recursive functions
(define (sum-1-to-N N)
(if (< N 1)
0
(+ N (sum-1-to-N (- N 1)))))
(define (my-member item lst)
(cond ((null? lst) #f)
((equal? item (car lst)) lst)
(else (my-member item (cdr lst)))))
53
Recursion vs. Iteration (Loops)
Tail Recursion is as efficient as
looping.
54
Just the factorial...
(define (fact n)
(if (= n 0)
1
(* n (fact (- n 1)))
)
)
• Recursion and runtime stack
55
Time
So to calculate...
Stack (space)
(fact 5)
(* 5 (fact 4))
(* 5 (* 4 (fact 3)))
(* 5 (* 4 (* 3 (fact 2))))
(* 5 (* 4 (* 3 (* 2 (fact 1)))))
(* 5 (* 4 (* 3 (* 2 (* 1 (fact 0))))))
.
.
(define (fact n)
(if (= n 0)
.
1
(* n (fact (- n 1)))
.
)
56
120
)
But we could use tail recursion
•a tail-recursive function is one in which the
recursive call occurs last
(define (tailfact n result) // help function
(if (= n 0)
Accumulating parameter
result
(tailfact (- n 1) (* n result))))
(define (fact n)
(tailfact n 1))
57
Time
Analysis
(fact 5)
(tailfact
(tailfact
(tailfact
(tailfact
(tailfact
(tailfact
120
Stack
5
4
3
2
1
0
1)
5)
20)
60)
120)
120)
58
But how does it work?
• Tail recursion requires two elements
– The tail recursive module must terminate
with a recursive call that leaves no work on
the stack to finish up. Any storage then
must be done in the parameter list as
opposed to the stack
– The interpreter or compiler must be
designed to recognize tail recursion and
handle it appropriately
59
Tail recursion is logically
equivalent to a loop!
Just put a goto in place of the
recursive call!!!
60
Rewrite in C
int tailfact(int n, int result)
{
if(n == 0)
{
Recall that this function
return result;
will be called like:
}
tailfact(5,1)
else
{
return tailfact(n - 1, result * n);
}
61
Put arg calcs into assignments
int tailfact(int n, int result)
{
if(n == 0)
return result;
else
{
result = result * n;
return tailfact(n - 1, result);
}
62
Put arg calcs into assignments
int tailfact(int n, int result)
{
if(n == 0)
return result;
else
{
result = result * n;
n = n - 1;
return tailfact(n, result);
}
63
Substitute goto beginning
in place of recursive call
int tailfact(int n, int result)
{
beginning:
if(n == 0)
return result;
else
{
result = result * n;
n = n - 1;
goto beginning;
}
64
Eliminate the goto
int tailfact(int n, int result)
{
while(1)
{
if(n == 0)
return result;
result = result * n;
n = n - 1;
}
return ERROR;
}
65
Nested Functions
(define (factorial N)
(define (factorial-help N value-so-far)
(if (zero? N)
value-so-far
(factorial-help (- N 1) (* N value-so-far))
)
)
(factorial-help N 1)
)
ƒsince factorial-help is defined inside of factorial, hidden to outside
66
Fibonacci numbers
fib(n) = 0
=1
= fib(n-1) + fib(n-2)
if n = 0
if n = 1
if n > 1
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))
67
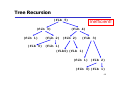
Tree Recursion
(fib 5)
(fib 3)
(fib 1)
Inefficient!
(fib 4)
(fib 2) (fib 2)
(fib 3)
(fib 0) (fib 1)
(fib0)(fib 1)
(fib 1) (fib 2)
(fib 0)(fib 1)
68
A Tail-Recursive Fib Function
(define (fib n) (ifib 1 0 n) )
(define (ifib next-fib cur-fib cnt)
(if (= cnt 0)
cur-fib
(ifib (+ next-fib cur-fib)
next-fib
(- cnt 1)
)
)
)
69
Polymorphism
Polymorphic functions can be applied to arguments of
different types
• function length is polymorphic:
¾ (length ‘(1 2 3))
value: 3
¾ (length ‘(a b c))
value: 3
¾ (length ‘((a) b (c d)))
value: 3
• function zero? is not polymorphic (monomorphic):
¾ (zero? 10)
value: #t
¾ (zero? ‘a)
error: object a is not the correct type
70