Download Variety1 Variety2 Variety3 Variety4

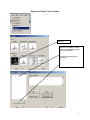
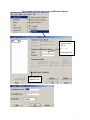
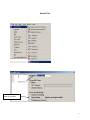
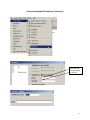
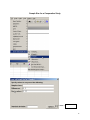
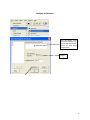
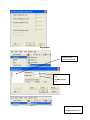
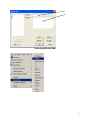
Diploma in Statistics: Laboratory 1
In this laboratory I want you to learn how to use Minitab for simple statistical
analyses. The interface is (in my view!) very simple, especially for anyone familiar
with Microsoft products, for example Excel. We will begin with the design and
analysis of simple comparative studies, using the data from the notes to explore
the Minitab facilities. Then we will analyse the melon varieties data discussed
when we studied ANOVA and the Ski-trails dataset which was examined when we
studied regression. Note that screenshots of most of the required operations are
attached to this handout.
Minitab works on data stored in a spreadsheet (worksheet). This sheet is static
(unlike Excel), it stores numbers or text, not formulae, so you cannot dynamically
change analyses. Most operations refer to data stored in columns (labelled c1,
c2…). The introductory example of a simple comparative study from Chapter 2 is
reproduced below.
1.
A study involved charging a spheroniser (essentially a centrifuge) with a dough-like
material and running it at two speeds (labelled A and B) to determine which gives
the higher yield. The yield is the percentage of the material that ends up as usable
pellets (the pellets are sieved to separate out and discard pellets that are either too
large or too small).
Speed-B
Speed-A
76.2
81.3
77.0
79.9
76.4
76.2
77.6
80.5
81.5
77.3
78.2
73.5
77.0
74.8
72.7
75.4
77.1
76.1
74.4
78.1
76.5
75.0
Table 1: Percentage yields for the two speeds
1
Type the data for Speed A and Speed B into two columns, say Speed A into c1
and Speed B into c2. In the header over the worksheet cells type Speed A into
Column 1 and Speed B into column 2.
Obtain descriptive statistics, Stat/ Basic Statistics/ Display descriptive
statistics, and dotplots, Graph/ Dotplot, of the data. (See screenshots, pages 5,
6)
Use the Stat/ Basic Statistics/ Two-sample t menu to obtain a t-test and
confidence interval for the long-run yield difference. (See screenshots, page 7)
The purpose of this session is learn how to use a statistics package to analyse
data. The objective is not just to push the right buttons! When you get output,
ask yourself if you know how the calculations were done. How do you interpret
each of the elements in the output?
2.
To check the model assumptions we usually obtain ‘residuals’ (what is ‘left-over’
when we subtract the group mean from each of the two sets of results) and
combine them into one set of values for analysis.
Use Calc/ calculator to calculate residuals (see page 8): c1-mean(c1) gives the
residuals for Method A. Store these in columns c3 (Method A) and c4 (Method B).
Stack the two columns in c5 either by copy and paste operations (either using the
Edit menu, or control-C copies selected cells and control-V pastes the values into
new cells) or by using Data/ Stack/ Columns. Obtain a Normal probability plot of
the residuals using Stat/ Basic Statistics / Normality Test (see page 9). Is the
Normality assumption reasonable?
3.
Use Stat/ Basic Statistics/ 2 Variances to carry out an F-test of the hypothesis
that the two long-run standard deviations are equal (see pages 10, 11).
4.
Now carry out the same analyses (apart from the residual analysis) for the
Epitaxial Layer study (attached, page 18); carry out the other analyses required in
the examination question. Note that the t-tests on summarised data are carried
out by selecting the “summarised data” part of the menu and filling in the data
summaries given on page 18. The one-sample analyses are done using menus
that are very similar to the two-sample analyses (see Stat/ Basic Statistics/ 1sample t). Note that when comparing two variances (SD squared) the menu
requires you to input the variances – not the SDs, as given in the exam question.
Analyse the Drivers dataset (attached, pages 19-20) using the Stat/ Basics
Statistics/ paired t- menu. Obtain the means and differences for each driver on
the two car designs using the Calc/ calculator menu. Plot differences against
2
means for each driver (use the Graph/ Scatterplot menu) and get a Normal plot of
the differences – do the model assumptions appear valid?
5.
Use the sample size facilities within Minitab (Stat/ Power and Sample Size) to
determine an appropriate sample size to detect a difference of (a) 0.5 (b) 1.0 (c)
1.5 units between two long-run means, when carrying out a two-tailed test using a
significance level of 0.05, while requiring a power of 0.95 and assuming the
standard deviation is either 1, 1.25, or 1.5 (see pages 12, 13).
6.
Mead and Curnow (1983) report an experiment to compare the yields of four
varieties of melon. Six plots of each variety were grown; the plots were allocated
to varieties at random. The yields (in kg) are shown below. Enter these into four
columns of the worksheet.
Variety1
25.1
17.3
26.4
16.1
22.2
15.9
Variety2
40.3
35.3
32.0
36.5
43.3
37.1
Variety3
Variety4
18.3
22.6
25.9
15.1
11.4
23.7
28.1
28.6
33.2
31.7
30.3
27.6
Page 14 gives screenshots based on the STAT/ ANOVA/ One-way (unstacked)
menu. Obtain the ANOVA table, carry out multiple comparisons (note: Tukey’s =
HSD, Fisher’s = LSD; Dunnett’s is another multiple comparison technique), get
residuals and fitted values and use them to check the model assumptions.
7.
Neter and Wasserman (1974) report the data below on a study of the relationship
between numbers of visitor days, Y, and numbers of miles, X, of intermediate level
ski trails in a sample of New England ski resorts during normal snow conditions.
The data are shown overleaf.
3
Miles-of-trails
10.5
2.5
13.1
4.0
14.7
3.6
7.1
22.5
17.0
6.4
Visitor Days
19929
5839
23696
9881
30011
7241
11634
45684
36476
12068
First, obtain a scatterplot of Visitor Days versus Miles-of-trails with a fitted line,
using Stat/ Regression/ Fitted Line Plot (see screenshots page 15). Next fit a
regression model getting full output, including a prediction and a confidence
interval when X = 10 miles of trails (type 10 into the “prediction intervals for new
observations” box of the Options sub-menu). Review what is available under the
various sub-menus (Graphs, Options, Storage, Results – see page 15). Store
residuals and fitted values and carry out the usual residual analyses. Interpret the
different elements of the output.
8.
To explore some of the graphical functions within Minitab we will first generate
some random data. Use the Calc/ Random Data/ Normal menu to generate 100
data values into a column – see screenshots page 16. Name the column N-data.
Just type it on the worksheet in the header row.
Use the Calc/ Random Data/ Chi-square menu to generate 100 data values from
a chi-square distribution with degrees of freedom equal to 7 into a column – see
screenshots page 17. Name the column Chi-data.
Now explore the Graph menu a little – for example you could get Histograms,
Dotplots and Boxplots of the two columns of data. In each case get both datasets
on the same graph – this makes it easier to make comparisons. I have not given
you screenshots – work it out for yourself! There is a help button on each submenu – see what you can learn from these (in particular look at the Boxplot Help
menu).
NOTE: THE COMMANDS AND SCREENSHOTS IN THIS HANDOUT ARE BASED ON MINITAB 15 –
MINITAB 16 IS NOW INSTALLED ON THE COLLEGE SYSTEM; THERE MAY BE MINOR DIFFERENCES
IN THE LATER VERSION.
4
Descriptive Statistics
Select the variables you
want either by
Highlighting and then
clicking on SELECT
or
Just Double-clicking on
the variable e.g.
C1 A
You can
change these
default
options by
selection/deselection
5
Dotplots for Data in Two Columns
SELECT
Select the variables you want
either by Highlighting and then
clicking on SELECT
or
Just Double-clicking on the
variable e.g.
C1 A
6
Two- Sample t-test for two groups in different columns
Click here first
and then double
click on
C1
A
Do the same for B
Select here for
standard T test
7
Calculating Residuals
This subtracts the mean
of column 1 from each
value in C1 and puts the
resulting numbers
(residuals) in C3
Do the same for C2 and put the resulting Residuals in C4. You can then cut and paste
the numbers in C3 and C4 and put them into C5 – C5 will them contain 22 values.
Name it Residuals by simply typing the name in the Minitab header.
An alternative way of stacking the residuals is as follows:
C1 A
C2 B
C3
C4
Select
Select C3 C4
or just Type
them
Type
Deselect
8
Normal Plot
These are alternative
tests for Normality
9
Comparing Standard Deviations (Variances)
Click here first
and then select
C1 and C2
10
Test for Equal Variances for Speed-B, Speed-A
F-Test
Test Statistic
P-Value
Speed-B
1.58
0.483
Levene's Test
Test Statistic
P-Value
Speed-A
1.0
1.5
2.0
2.5
3.0
3.5
95% Bonferroni Confidence Intervals for StDevs
0.53
0.477
4.0
The standard F-test
assumes data
Normality. Levene’s
is an alternative test
that does not make
this assumption.
Speed-B
Speed-A
Boxplots of the
two data columns
72
74
76
78
80
82
Data
Extract from Minitab HELP Menu:
Boxplots summarize information about the shape, dispersion, and center of your data.
They can also help you spot outliers.
·
The left edge of the box represents the first quartile (Q1), while the right edge
represents the third quartile (Q3). Thus the box portion of the plot represents the
interquartile range (IQR), or the middle 50% of the observations.
·
The line drawn through the box represents the median of the data.
·
The lines extending from the box are called whiskers. The whiskers extend
outward to indicate the lowest and highest values in the data set (excluding outliers).
·
Extreme values, or outliers, are represented by dots. A value is considered an
outlier if it is outside of the box (greater than Q3 or less than Q1) by more than 1.5 times
the IQR.
Note: Bonferroni confidence intervals mean that we are 95% confident that both
intervals simultaneously cover the two population parameters, here 1 and 2.
11
Sample Size for a Comparative Study
See overleaf
12
Power and Sample Size
2-Sample t Test
Testing mean 1 = mean 2 (versus not =)
Calculating power for mean 1 = mean 2 + difference
Alpha = 0.05 Assumed standard deviation = 1
Sample Target
Difference Size Power Actual Power
0.5 105 0.95
0.950129
Note that the actual power can be a bit different from that specified as your target
value since the sample size is discrete, i.e., we can choose sample sizes of say, 104,
105 or 106 but not intermediate non-integer values.
13
Analysis of Variance
Put the Melons data
into four columns, e.g.
C5-C8 and then select
them so that they
appear here
Select
14
Regression
Put data into two
columns beforehand
Put visitor days
here
Put Miles of trail
here
Put visitor days here
Put Miles of trail here
15
Generating Random Data
16
17
100 rows into
C2 (say)
7
Examination-style Question
1.
A first step in processing silicon wafers for integrated circuit devices is to grow an
epitaxial layer on the polished silicon wafers. The manufacturing specifications
for a particular product are that the epitaxial layer should be between 10 µm and
18 µm thick. Two production lines produce these wafers. Samples of 25 wafers
from the two lines gave the results tabulated below, when their epitaxial layers
were measured.
Mean
Standard Deviation
Line 1
Line 2
14.3
16.4
0.80
0.75
18
Assume layer thickness is Normally distributed.
(a)
Carry out a statistical test of the hypothesis that the long-run average
thickness of layers produced on line 1 equals the mid-specification value
of 14 µm. Interpret the result of your test.
(5 marks)
(b)
Calculate and interpret a 95% confidence interval for the long-run average
thickness of layers produced on line 2.
(4 marks)
(c)
Carry out a statistical test of the hypothesis that the long-run average
layer thicknesses are the same for lines 1 and 2 and interpret the result of
the test.
(d)
(6 marks)
Calculate and interpret a 95% confidence interval for the difference
between the long-run average layer thicknesses from lines 1 and 2.
(6 marks)
Examination Question: Q1 Hilary, 2008
1.
A study of engineering design factors that affect the handling ability of differently
designed cars involved twelve drivers parallel parking two cars of different
design. The data are shown below; the responses are the times (in seconds) to
complete the parking operation under standardized test conditions. The order in
which the cars were driven was randomized separately for each driver.
Driver
Design 1
Design 2
1
42.0
17.8
2
30.7
20.2
19
(a)
3
21.2
16.8
4
29.2
41.4
5
27.1
21.3
6
38.4
38.5
7
28.8
16.9
8
63.2
32.2
9
38.6
27.7
10
29.4
23.1
11
28.3
29.6
12
26.2
20.5
A paired t-test gave a t-value of t=2.48. How was this value calculated? What
are the number of degrees of freedom and the critical values for a t-test using a
significance level of 0.05?
Interpret the result of the test.
Calculate the
corresponding 95% confidence interval and explain its interpretation in this
context. What model underlies the analysis?
[10 marks]
(b)
A two-sample t-test gave a t-value of t=2.02. How was this value calculated?
What are the number of degrees of freedom and the critical values for a t-test
using a significance level of 0.05? Interpret the result of the test. Calculate the
corresponding 95% confidence interval and explain its interpretation in this
context. What model underlies the analysis?
[10 marks]
(c)
Why is the result of the test carried for part (b) different from the result of that for
part (a). Which analysis do you consider more appropriate and why?
[5 marks]
20
21