* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download A Test for Normality
Survey
Document related concepts
Transcript
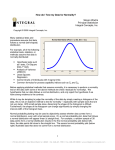
A Test for Normality When a sample size is small, we have assumed that we are sampling from a normal population. How can we test this assumption? We can test this hypotheses: Ho : The population distribution is normal HA : The population distribution is not normal On pages 584 -585 there is a test for normality, the Ryan-Joiner test. Here is how you can use Minitab to perform the test: 1. Enter your data in any column 2. From the Minitab menu choose Stat Basic Statistics Normality test 3. Choose the column that contains your data and also select Ryan-Joiner, click OK 3. You will see a “probability plot.” If the data comes from a population that is close to normal, the points will cluster around a line as they do below: Notice that Minitab gives you the p-value for the test. In this example, the p value is greater than .10. So we would NOT reject the null hypothesis. And our data does not indicate that the population is not normal. Here is another example: Probability Plot of C2 Normal 99.99 Mean StDev N RJ P-Value 99 Percent 95 54.77 25.97 1000 0.979 <0.010 80 50 20 5 1 0.01 -50 0 50 C2 100 150 The p-value is less than .01—so here we would reject the null Hypothesis and we have evidence to believe that the population is not normal…the test is significant