Download A Test for Normality

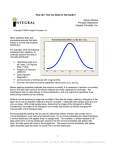
A Test for Normality
When a sample size is small, we have assumed that we are sampling from a normal
population. How can we test this assumption?
We can test this hypotheses:
Ho : The population distribution is normal
HA : The population distribution is not normal
On pages 584 -585 there is a test for normality, the Ryan-Joiner test. Here is how you
can use Minitab to perform the test:
1. Enter your data in any column
2. From the Minitab menu choose Stat  Basic Statistics Normality test
3. Choose the column that contains your data and also select Ryan-Joiner, click
OK
3. You will see a “probability plot.” If the data comes from a population that is close
to normal, the points will cluster around a line as they do below:
Notice that Minitab gives you the p-value for the test. In this example, the p value is
greater than .10. So we would NOT reject the null hypothesis. And our data does not
indicate that the population is not normal.
Here is another example:
Probability Plot of C2
Normal
99.99
Mean
StDev
N
RJ
P-Value
99
Percent
95
54.77
25.97
1000
0.979
<0.010
80
50
20
5
1
0.01
-50
0
50
C2
100
150
The p-value is less than .01—so here we would reject the null Hypothesis and we
have evidence to believe that the population is not normal…the test is significant