Download Transforming data lecture notes

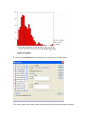
WEEK 3: NORMALITY AND TRANSFORMING
DATA
In this session we will review the issue of normality and transforming data.
We will be using a data file that was created by randomly sampling 400 elementary
schools from the California Department of Education's API 2000 dataset. This data file
contains a measure of school academic performance as well as other attributes of the
elementary schools, such as, class size, enrollment, poverty, etc.
So, let us explore the distribution of our variables and how we might transform them to a
more normal shape. Let's start by making a histogram of the variable enroll data.
Graphs/Histogram…
We can use the normal option to superimpose a normal curve on this graph.
We can see quite a discrepancy between the actual data and the superimposed normal

We can use the EXPLORE command to get a boxplot, stem and leaf plot,
histogram, and normal probability plots (with tests of normality) as shown below.
There are a number of things indicating this variable is not normal:



The skewness indicates it is positively skewed (since it is greater than 0),
Both of the tests of normality are significant (suggesting enroll is not normal).
If enroll was normal, the red boxes on the Q-Q plot would fall along the green
line, but instead they deviate quite a bit from the green line.
Case Processing Summary
Cases
Valid
Missing
Total
N Percent N Percent N Percent
ENROLL 400 100.0% 0
.0% 400 100.0%
Descriptives
Statistic
Std.
Error
483.47
Mean
95% Confidence Interval for
Mean
Lower
Bound
461.21
Upper
Bound
505.72
5% Trimmed Mean
465.70
Median
435.00
51278.871
ENROLL Variance
Std. Deviation
226.448
Minimum
130
Maximum
1570
Range
1440
290.00
Interquartile Range
Skewness
1.349
.122
Kurtosis
3.108
.243
Tests of Normality
Kolmogorov-Smirnov(a)
Statistic
ENROLL
11.322
.097
df
400
Shapiro-Wilk
Sig. Statistic df Sig.
.000
a Lilliefors Significance Correction
.914 400 .000
number of students Stem-and-Leaf Plot
Frequency
Stem &
4.00
1
15.00
1
29.00
2
29.00
2
47.00
3
46.00
3
38.00
4
27.00
4
31.00
5
28.00
5
29.00
6
21.00
6
15.00
7
9.00
7
9.00
8
3.00
8
3.00
9
1.00
9
7.00
10
9.00 Extremes
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Leaf
3&
5678899
0011122333444
5556667788999
00000011111222223333344
5555566666777888899999
000000111111233344
5556666688999&
00111122223444
5556778889999
00011112233344
555677899
001234
667&
13&
5&
2&
&
00&
(>=1059)
Stem width:
100
Each leaf:
2 case(s)
& denotes fractional leaves.
Transformation
Given the skewness to the right in enroll, let us try a log transformation to see if that
makes it more normal. Below we create a variable lenroll that is the natural log of enroll.
Go to TRANSFORM/COMPUTE.
We then we repeat the EXPLORE command.
Case Processing Summary
Cases
Valid
Missing
Total
N Percent N Percent N Percent
LENROLL 400 100.0% 0
.0% 400 100.0%
Descriptives
Statistic Std. Error
6.0792
Mean
95% Confidence Interval for Mean
Lower Bound
6.0345
Upper Bound
6.1238
5% Trimmed Mean
6.0798
Median
6.0753
.207
Variance
.45445
LENROLL Std. Deviation
Minimum
4.87
Maximum
7.36
Range
2.49
Interquartile Range
.6451
Skewness
-.059
.122
Kurtosis
-.174
.243
Tests of Normality
Kolmogorov-Smirnov(a)
Statistic
LENROLL
.02272
.038
df
400
Shapiro-Wilk
Sig. Statistic df Sig.
.185
a Lilliefors Significance Correction
.996 400 .485
LENROLL Stem-and-Leaf Plot
Frequency
4.00
6.00
19.00
32.00
48.00
67.00
55.00
63.00
60.00
26.00
13.00
4.00
3.00
Stem width:
Each leaf:
Stem &
4
5
5
5
5
5
6
6
6
6
6
7
7
.
.
.
.
.
.
.
.
.
.
.
.
.
Leaf
89
011
222233333
444444445555555
666666667777777777777777
888888888888888899999999999999999
000000000000001111111111111
2222222222222222333333333333333
44444444444444444455555555555
6666666677777
889999
0&
3
1.00
2 case(s)
& denotes fractional leaves.
The indications are that lenroll is much more normally distributed -- its skewness and
kurtosis are near 0 (which would be normal), the tests of normality are non-significant,
the histogram looks normal, and the red boxes on the Q-Q plot fall mostly along the
green line. Taking the natural log of enrollment seems to have successfully produced a
normally distributed variable.
THREE DATA TRANSFORMATION
This section is intended to give a brief refresher on what really happens when one applies
a data transformation.
Square root transformation. Most readers will be familiar with this procedure. When one
applies a square root transformation, the square root of every value is taken. However, as
one cannot take the square root of a negative number, if there are negative values for a
variable, a constant must be added to move the minimum value of the distribution above
0, preferably to 1.00 (the rationale for this assertion is explained below). Another
important point is that numbers of 1.00 and above behave differently than numbers
between 0.00 and 0.99. The square root of numbers above 1.00 always become smaller,
1.00 and 0.00 remain constant, and number between 0.00 and 1.00 become larger (the
square root of 4 is 2, but the square root of 0.40 is 0.63). Thus, if you apply a square root
to a continuous variable that contains values between 0 and 1 as well as above 1, you are
treating some numbers differently than others, which is probably not desirable in most
cases.
Log transformation(s). Logarithmic transformations are actually a class of
transformations, rather than a single transformation. In brief, a logarithm is the power
(exponent) to which a base number must be raised in order to get the original number.
Any given number can be expressed as y to the x power in an infinite number of ways.
For example, if we were talking about base 10, 1 is 100, 100 is 102, 16 is 101.2, and so
on. Thus, log10(100)=2 and log10(16)=1.2. However, base 10 is not the only option for
log transformations. Another common option is the Natural Logarithm, where the
constant e (2.7182818) is the base. In this case the natural log 100 is 4.605. As the
logarithm of any negative number or number less than 1 is undefined, if a variable
contains values less than 1.0, a constant must be added to move the minimum value of the
distribution, preferably to 1.00.
There are good reasons to consider a range of bases. Cleveland (1984) argues that base
10, 2, and e should always be considered at a minimum. For example, in cases in which
there are extremes of range, base 10 is desirable, but when there are ranges that are less
extreme, using base 10 will result in a loss of resolution, and using a lower base (e or 2)
will serve. (Higher bases tend to pull extreme values in more drastically than lower
bases). Readers are encouraged to consult Cleveland (1984) for more details.
Inverse transformation. To take the inverse of a number (x) is to compute 1/x. What this
does is essentially make very small numbers very large, and very large numbers very
small. This transformation has the effect of reversing the order of your scores. Thus, one
must be careful to reflect, or reverse the distribution prior to applying an inverse
transformation. To reflect, one multiplies a variable by -1, and then adds a constant to the
distribution to bring the minimum value back above 1.0. Then, once the inverse
transformation is complete, the ordering of the values will be identical to the original
data.
In general, these three transformations have been presented in the relative order of power
(from weakest to most powerful). A good guideline is to use the minimum amount of
transformation necessary to improve normality.
Exercise on transforming data
Test the continuous variables in the SPSS file for normality and transform where
appropriate.