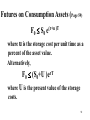Download F t (k)

Determination of
Forward and Futures
Prices
Chapter 3
0
• Arbitrage:
A market situation whereby an investor
can make a profit with: no equity and
no risk.
• Efficiency:
A market is said to be efficient if prices
are such that there exist no arbitrage
opportunities.
Alternatively, a market is said to be
inefficient if prices present arbitrage
opportunities for investors in this
market.
1
SHORT SELLING STOCKS
An Investor may call a broker and ask to “sell a
particular stock short.”
This means that the investor does not own shares of the
stock, but wishes to sell it anyway.
The investor speculates that the stock’s share price will
fall and money will be made upon buying the shares
back at a lower price. Alas, the investor does not own
shares of the stock. The broker will lend the investor
shares from the broker’s or a client’s account and sell
it in the investor’s name. The investor’s obligation is to
hand over the shares some time in the future, or upon
the broker’s request.
2
SHORT SELLING STOCKS
Other conditions:
The proceeds from the short sale cannot be
used by the short seller. Instead, they are
deposited in an escrow account in the
investor’s name until the investor makes good
on the promise to bring the shares back.
Moreover, the investor must deposit an
additional amount of at least 50% of the
short sale’s proceeds in the escrow account.
This additional amount guarantees that there is
enough capital to buy back the borrowed
shares and hand them over back to the
broker, in case the shares price increases.3
SHORT SELLING STOCKS
There are more details associated with short
selling stocks. For example, if the stock pays
dividend, the short seller must pay the
dividend to the lender. Moreover, the short
seller does not gain interest on the amount
deposited in the escrow account, etc.
We will use stock short sales in many of
strategies associated with derivatives.
In terms of cash flows:
St
is the cash flow from selling the
stock short on date t.
-ST is the cash flow from purchasing the
back on date T.
4
• Risk-Free Asset: is a security of
investment whose return carries no risk.
Thus, the return on this security is known
and guaranteed in advance.
• Risk-Free Borrowing And Landing:
By purchasing the risk-free asset,
investors lend their capital and earn the
risk-free rate.
By selling the risk-free asset, investors
borrow capital at the risk-free rate.
5
• The One-Price Law:
There exists only one risk-free rate in
an efficient economy.
Continuous Compounding and
Discounting:
Calculating the future value of a
series of cash flows or, the present
value of the cash flows, respectively,
in a continuous time framework.
6
Compounded Interest
Any principal amount, P, invested at an annual
interest rate, r, compounded annually, for T
years would grow to AT = P(1 + r)T.
If compounded Quarterly:
AT = P(1 +r/4)4T.
In general, with m compounding periods every
year, the periodic rate becomes r/m and
mT is the number of compounding periods.
Thus, P grows to:
AT = P(1 +r/m)mT.
7
Monthly compounding becomes:
AT = P(1 +r/12)12T
and daily compounding yields:
AT = P(1 +r/365)365T
Eample: T =10 years; r =12%; P = $100.
1. Simple annual compounding yields:
A10 = $100(1+ .12)10 = $310.58
2. Monthly compounding yields:
A10 = $100(1 + .12/12)120 = $330.03
3. Daily compounding yields:
A10 = $100(1 + .12/365)3,650 = $331.94.
8
In the early 1970s, banks came up with the following
economic reasoning: Since the bank has depositors’
money all the time, this money should be working for
the depositor all the time!
This idea, of course, leads to the concept of
continuous compounding.
r

A T  P1  
 m
mT
Observe that continuous time means that the number
of compounding periods every year, m, increases
without limit. This implies that the length of every
compounding time period goes to zero and thus, the
periodic interest rate, r/m, becomes smaller and
smaller.
9
This reasoning implies that we need to solve:
mT
r 

A T  Limit {P 1   }
m 
 m m
( ) rT
r


1 

A T  (P)Limit { 1 
}.
 m 
m 
r

The solution of this limit yields
the expression for the continuous ly
compounded value of P after T years :
A T  Pe .
rT
10
EXAMPLE, continued: First, recall that:
x
1

e  Limit {1   }
x 
x

example: x
e
1
2
10
2.59374246
1,000
2.71692393
10,000
2.71814592
In the limit e = 2.718281828…
11
EXAMPLE, continued: Recall that in
our example: T= 10 years and r = 12% and
P=$100. Thus, P=$100 invested at an annual
rate of 12%. will grow to by the factor:
Compounding
Factor
Simple
3.105848208
Quarterly
3.262037792
Monthly
3.300386895
Daily
3.319462164
Continuously
3.320116923
12
Given A T , r and T, the continuous ly
discounted value of A T is :
P  ATe
- rT
.
For any time period t cash flow, CFt ,
can be continuous ly discounted
for the present by multiplyin g it by
- rt
e ,
where r is the continuous ly compounded
interest rate.
13
Continuous Compounding
(Page 43)
• In the limit as we compound more and
more frequently we obtain continuously
compounded interest rates.
• $100 grows to $100eRT when invested at
a continuously compounded rate R for
time T.
• $100 received at time T discounts to
$100e-RT at time zero when the
continuously compounded discount rate
14
is R.
Conversion Formulas (Page 44)
Define
Rc : continuously compounded rate
Rm: same rate with compounding m
times per year
Rm 

R c  mln 1 

m 

R c /m
Rm  m e
1


15
FUTURES and SPOT PRICES:
AN ECONOMICS MODEL of
DEMAND and SUPPLY
SPECULATORS: WILL OPEN RISKY FUTURES
POSITIONS FOR EXPECTED PROFITS.
HEDGERS: WILL OPEN FUTURES POSITIONS IN
ORDER TO ELIMINATE ALL PRICE RISK.
ARBITRAGERS: WILL OPEN SIMULTANEOUS
FUTURES AND CASH POSITIONS IN ORDER TO
16
MAKE ARBITRAGE PROFITS.
HEDGERS:
HEDGERS TAKE FUTURES POSITIONS IN ORDER
TO ELIMINATE PRICE RISK.
THERE ARE TWO TYPES OF HEDEGES
A LONG HEDGE
TAKE A LONG FUTURES POSITION IN ORDER TO LOCK
IN THE PRICE OF AN ANTICIPATED PURCHASE AT A
FUTURE TIME
A SHORT HEDGE
TAKE A SHORT FUTURES POSITION IN ORDER TO
LOCK IN THE SELLING PRICE OF AN ANTICIPATED
SALE AT A FUTURE TIME.
17
ARBITRAGE WITH FUTURES:
SPOT
MARKET
FUTURES MARKET
Contract to buy the product
LONG futures
Contract to sell the product
SHORT futures
18
Long hedgers want to hedge a decreasing amount of
their risk exposure as the premium of the settlement
price over the expected future spot price increases.
Ft (k)
a
b
Expt [St+k]
c
0
Od
Long hedgers want to
hedge all of their risk
exposure
if
the
settlement price is less
than or equal to the
expected future spot
price.
Quantity of long
positions
Demand for LONG futures positions by long
HEDGERS
19
Ft (k)
d
e
Expt [St + k]
f
0
Short hedgers want to
hedge all of their risk
exposure
if
the
settlement price is
greater than or equal
to the expected future
spot price.
Short hedgers want to hedge a
decreasing amount of their
risk exposure as the discount
of the settlement price below
the expected future spot price
increases.
QS
Quantity of short
positions
Supply of SHORT futures positions by
short HEDGERS.
20
Ft (k)
S
Supply
schedule
D
Ft (k)e
Premium
Expt [St + k]
Demand
schedule
S
D
0
QS
Qd
Quantity of
positions
Equilibrium in a futures market with a
preponderance of long hedgers.
21
Ft (k)
S
D
Supply schedule
Expt [St + k]
Discount
Ft (k)e
Demand schedule
S
0
D
Qd
QS
Quantity of
positions
Equilibrium in a futures market with a
preponderance of short hedgers.
22
Ft (k)
Speculators will not demand any long
positions if the settlement price
exceeds the expected future spot price.
a
Expt [St + k]
b
Speculators demand more long
positions the greater the
discount of the settlement price
below the expected future spot
price.
c
0
Quantity of long
positions
Demand for long positions in futures
contracts by speculators.
23
Ft (k)
d
Expt [St + k]
Speculators supply more short
positions
the
greater the
premium of the settlement price
over the expected future spot
price
e
f
0
Speculators will not supply any short
positions if the settlement price is
below the the expected future spot
price
Quantity of short
positions
Supply of short positions in futures contracts
by speculators.
24
Ft (k)
S
D
Expt [St + k]
Ft (k)e
Increased
supply from
speculators
Discount
Increased demand
from speculators
S
0
D
Qd QE Qs
Quantity of
positions
Equilibrium in a futures market with
speculators and a preponderance of short
hedgers.
25
Ft (k)
S
Increased
supply from
speculators
D
Ft (k)e
Increased demand
from speculators
Premium
Expt [St + k]
S
D
0
QE
Quantity of
positions
Equilibrium in a futures market with
speculators and a preponderance of long
hedgers.
26
Excess supply of the asset
when the spot market price is
St
Spot supply
}
Ft (k); St
Ft (k)e
Premium
Expt [St + k]
Spot demand
0
QE
Quantity of the asset
Equilibrium in the spot market
27
Ft (k)
Expt [St + k]
Schedule of excess demand by
hedgers and speculators
Premium
}
Ft (k)e
Excess demand for long positions by
hedgers and speculators when the
settlement price is Ft (k)e
0
Q
Net quantity of long positions held by
hedgers and speculators
Equilibrium in the futures market
28
ARBITRAGE
IN PERFECT MARKETS
CASH -AND-CARRY
DATE
SPOT MARKET
FUTURES MARKET
NOW
1. BORROW CAPITAL.
3. SHORT FUTURES.
2. BUY THE ASSET IN THE
SPOT MARKET AND CARRY
IT TO DELIVERY.
DELIVERY
1. REPAY THE LOAN
3. DELIVER THE STORED
COMMODITY TO CLOSE
THE SHORT FUTURES
POSITION
29
ARBITRAGE
IN PERFECT MARKETS
REVERSE CASH -AND-CARRY
DATE
SPOT MARKET
NOW
1. SHORT SELL ASSET
FUTURES MARKET
3. LONG FUTURES
2. INVEST THE PROCEEDS
IN GOV. BOND
DELIVERY: 2. REDEEM THE BOND
3. TAKE DELIVERY
ASSET TO CLOSE
THE LONG
FUTURES
POSITION
1. CLOSE THE SPOT SHORT POSITION
30
Notation
S0: Spot price today. (Or St)
F0,T: Futures or forward price today for
delivery at T. ( or Ft,T)
T: Time until delivery date
r: Risk-free interest rate for delivery
date.
31
Gold Example (From Chapter 1)
• For gold
F0 = S0(1 + r )T
(assuming no storage costs)
• If r is compounded continuously
instead of annually
F0 = S0erT
PROOF:
32
ARBITRAGE
IN PERFECT MARKETS
CASH -AND-CARRY
DATE
SPOT MARKET
FUTURES MARKET
NOW
1. BORROW CAPITAL: S0
3. SHORT FUTURES
2. BUY THE ASSET IN
F0,T
THE SPOT MARKET
AND CARRY IT TO DELIVERY
DELIVERY
1. REPAY THE LOAN
3. DELIVER THE STORED
COMMODITY TO CLOSE
THE SHORT FUTURES
POSITION
S0erT

F0,T
33
ARBITRAGE
IN PERFECT MARKETS
REVERSE CASH -AND-CARRY
DATE
SPOT MARKET
FUTURES MARKET
NOW
1. SHORT SELL ASSET: S0
3. LONG FUTURES
2. INVEST THE PROCEEDS
F0,T
IN GOV. BOND
DELIVERY:
2. REDEEM THE BOND
3. TAKE DELIVERY
ASSET TO CLOSE
THE LONG FUTURES
POSITION
1. CLOSE THE SPOT SHORT POSITION
S0erT

F0,T
34
Extension of the Gold Example
(Page 46, equation 3.5)
• For any investment asset that provides no
income and has no storage costs
F0 = S0erT
35
When an Investment Asset
Provides a Known Dollar
Income (page 48, equation 3.6)
F0 = (S0 – I )erT
where I is the present value of
the income
36
When an Investment Asset Provides
a Known Yield
(Page 49, equation 3.7)
F0 = S0e(r–q )T
where q is the average yield during the life
of the contract (expressed with continuous
compounding)
37
Valuing a Forward Contract
Page 50
• Suppose that K is delivery price in a forward
contract, F0,T is forward price today for delivery
at T
• The value of a long forward contract, ƒ, is
ƒ = (F0,T – K )e–rT
• Similarly, the value of a short forward contract is
(K – F0,T )e–rT
38
Forward vs Futures Prices
• Forward and futures prices are usually
assumed to be the same. When interest
rates are uncertain they are, in theory,
slightly different:
• A strong positive correlation between
interest rates and the asset price implies
the futures price is slightly higher than
the forward price
• A strong negative correlation implies the
reverse
39
Stock Index (Page 52)
• Can be viewed as an investment asset
paying a dividend yield
• The futures price and spot price
relationship is therefore
F0 = S0e(r–q )T
where q is the dividend yield on the
portfolio represented by the index
40
Stock Index (continued)
• For the formula to be true it is
important that the index represent an
investment asset
• In other words, changes in the index
must correspond to changes in the
value of a tradable portfolio
• The Nikkei index viewed as a dollar
number does not represent an
investment asset
41
Index Arbitrage
• When F0>S0e(r-q)T , an arbitrageur buys
the stocks underlying
the index and sells
futures.
• When F0<S0e(r-q)T , an arbitrageur buys
futures and shorts or
sells the stocks
underlying the index.
42
Index Arbitrage (continued)
• Index arbitrage involves simultaneous
trades in futures and many different
stocks
• Very often a computer is used to
generate the trades
• Occasionally (e.g., on Black Monday)
simultaneous trades are not possible
and the theoretical no-arbitrage
relationship between F0,T and S0 does
not hold
43
Futures and Forwards on
Currencies (Page 55-58)
• A foreign currency is analogous to a
security providing a dividend yield
• The continuous dividend yield is the
foreign risk-free interest rate
• It follows that if rf is the foreign riskfree interest rate
(r  r )T
f
F0,T  S0e
44
THE INTEREST RATES PARITY
Wherever financial flows are unrestricted, exchange rates,
the forward rates and the interest rates in any two countries
must maintain a NO- ARBITRAGE relationship:
Interest Rates Parity.
F(FCDOM /FC) = S(FC DOM /FC)e
(rDOM - rFOR )(T - t)
45
.
NO ARBITRAGE: CASH-AND-CARRY
TIME
CASH
FUTURES
t
(1) BORROW $A. rDOM
(4) SHORT FOREIGN CURRENCY
(2) BUY FOREIGN CURRENCY
FORWARD
A/S($/FC) [=AS(FC/$)]
Ft,T($/FC)
AMOUNT:
(3) INVEST IN BONDS
AS(FC/$)e
DENOMINATED IN THE
rFOR (T -t)
FOREIGN CURRENCY rFOR
T
(3) REDEEM THE BONDS
rFOR (T -t)
EARN
(4) DELIVER THE CURRENCY TO
(1) PAY BACK THE LOAN
RECEIVE:
AS(FC/$)e
Ae rDOM (T -t)
CLOSE THE SHORT POSITION
F($/FC)AS(FC/$)e
rFOR (T - t)
IN THE ABSENCE OF ARBITRAGE:
Ae
rD (T  t)
 F($/FC)AS(FC/$)e
Ft,T ($/FC)  St ($/FC)e
rFOR (T-t)
(rDOM - rFOR )(T- t)
46
NO ARBITRAGE:
REVERSE CASH – AND - CARRY
TIME
CASH
FUTURES
t
(1) BORROW FC A. rFOR
(4) LONG FOREIGN CURRENCY
(2) BUY DOLLARS
AS($/FC)
(3) INVEST IN T-BILLS
FORWARD Ft,T($/FC)
AMOUNT IN DOLLARS:
AS($/FC)e
R DOM (T - t)
FOR RDOM
T
REDEEM THE T-BILLS
EARN
AS($/FC)e rDOM (T-t)
PAY BACK THE LOAN
Ae
TAKE DELIVERY TO CLOSE
THE LONG POSITION
RECEIVE
rFOR (T - t)
Ae
IN THE ABSENCE OF ARBITRAGE:
rDOM ( T-t)
AS($/FC)e
F($/FC)
rFOR (T - t)  AS($/FC)e
rDOM ( T- t)
F($/FC)
Ft,T ($/FC)  St ($/FC)e
(rDOM rFOR )( T- t)
47
FROM THE CASH-AND-CARRY STRATEGY:
(rDOM - rFOR )(T - t)
t,T
t
F ($/FC) S ($/FC)e
FROM THE REVERSE CASH-AND-CARRY STRATEGY:
(rDOM - rFOR )(T - t)
t,T
t
F ($/FC)  S ($/FC)e
THE ONLY WAY THE TWO INEQUALITIES HOLD
SIMULTANEOUSLY IS BY BEING AN EQUALITY:
Ft,T ($/FC) = St ($/FC)e
(rDOM - rFOR )(T - t)
48
ON MAY 25 AN ARBITRAGER OBSERVES THE FOLLOWING MARKET PRICES:
S(USD/GBP) = 1.5640 <=> S(GBP/USD) = .6393
F(USD/GBP) = 1.5328 <=> F(GBP/USD) = .6524
RUS = 7.85% ; RGB = 12%
FTheoretical = 1.5640e
(.0785 - .12)
209
365
= 1.5273
CASH AND CARRY
TIME
MAY 25
CASH
(1) BORROW USD100M AT 7. 85%
FOR 209 DAYS
FUTURES
SHORT GBP 68,477,215 FORWARD
FOR DEC. 20, FOR USD1.5328/GBP
(2) BUY GBP63,930,000
(3) INVEST THE GBP63,930,000
IN BRITISH BONDS
DEC 20
RECEIVE GBP68,477,215
209
.12
365
63,930,000e
= GBP68,477, 215
DELIVER GBP68,477,215
FOR USD104,961,875.2
REPAY YOUR LOAN:
209
.0785
365
100Me
= USD104,597,484.3
ARBITRAGE PROFIT: USD104,961,875.2 - USD104,597,484.3 = USD364,390.90
49
Futures on Consumption Assets (Page 59)
F0  S0 e(r+u )T
where u is the storage cost per unit time as a
percent of the asset value.
Alternatively,
F0  (S0+U )erT
where U is the present value of the storage
costs.
50
The Cost of Carry (Page 60)
• The cost of carry, c, is the storage cost
plus the interest costs less the income
earned.
• For an investment asset F0 = S0ecT
• For a consumption asset F0 = S0ecT
• The convenience yield on the
consumption asset, y, is defined
so that F0 = S0 e(c–y )T
51
ARBITRAGE IN THE REAL WORLD
TRANSACTION COSTS
DIFFERENT BORROWING AND LENDING RATES
MARGINS REQUIREMENTS
RESTRICTED SHORT SALES AN USE OF PROCEEDS
STORAGE LIMITATIONS
*
BID - ASK SPREADS
**
MARKING - TO - MARKET
*
BID - THE HIGHEST PRICE ANY ONE IS WILLING TO BUY AT NOW
**
ASK - THE LOWEST PRICE ANY ONE IS WILLING TO SELL AT
NOW.
MARKING - TO - MARKET: YOU MAY BE FORCED TO CLOSE YOUR
POSITION BEFORE ITS MATURITY.
52
FOR THE CASH - AND - CARRY:
BORROW AT THE BORROWING RATE: rB
BUY SPOT FOR:
SASK
SELL FUTURES AT THE BID PRICE:
F(BID).
PAY TRANSACTION COSTS ON:
BORROWING
BUYING SPOT
SELLING FUTURES
PAY CARRYING COST
PAY MARGINS
53
THE REVERSE CASH - AND - CARRY
SELL SHORT IN THE SPOT FOR:
SBID.
INVEST THE FACTION OF THE PROCEEDS
ALLOWED BY LAW: f;
0 ≦ f ≦ 1.
LEND MONEY (INVEST) AT THE LENDING RATE:
LONG FUTURES AT THE ASK PRICE:
F(ASK).
PAY TRANSACTION COST ON:
SHORT SELLING SPOT
LENDING
BUYING FUTURES
PAY MARGIN
54
rL
With these market realities, a new no-arbitrage condition emerges:
BL < F < BU
As long as the futures price fluctuates between the bounds
there is no possibility to make arbitrage profits
BU
BL
BU
F
BL
time
55
Example
S0,BID (1 - c)[1 + f(rBID )] < F0, t < S0,ASK (1 + c)(1 + rASK)
c is the % of the price which is a transaction cost.
Here, we assume that the futures trades for one price.
In order to understand the LHS of the inequality,
remember that the rule in the USA is that you may
invest only a fraction, f, of the proceeds from a short
sale. So, in the reverse cash and carry, the arbitrager
sells the asset short at the bid price. Then (1-f)S0,BID
cannot be invested while fS0,BID(1+rBID) is invested.
Thus, the inequality becomes:
F0,T  (1-f)S0 + fS0(1+rBID)
F0,T  S0(1 + frBID)
56
EXAMPLE 1.
S0,BID (1 - T)[1 + f(rL )] < F0, t < S0,ASK (1 + T)(1 + rB)
S0,ASK = $20.50 / bbl
S0,BID = $20.25 / bbl
rASK
= 12 %
rBID = 8 %
c = 3%
$20.25(.97)[1+f(.08)]<F0,t< $20.50(1.03)(1.12)
$19.6425 + f($1.57) < F0,t < $23.6488
DEPENDING ON f, ANY FUTURES PRICE BETWEEN THE TWO LIMITS WILL
LEAVE NO ARBITRAGE OPPORTUNITIES. THE CASH-AND-CARRY WILL
COST $23.6488/bbl. THE REVERSE CASH-AND-CARRY WILL COST 19.6425
+ f(1.62). IF f=0.5 THE LOWER BOUND IS $20.45. IN THE REAL MARKET, f
= 1, FOR SOME LARGE ARBITAGE FIRMS AND THEIR LOWER BOUND IS
$21.26. THUS, IT IS CLEAR THAT THERE ARE DIFFERENT ARBITRAGE
BOUNDS APPLICABLE TO DIFFERENT INVESTORS. THE TIGHTER THE
BOUNDS, THE GREATER ARE THE ARBITRAGE OPPORTUNITIES.
57
Example 2.: THE INTEREST RATES PARITY
In the real markets, buyers pay the ask
price while sellers receive the bid price.
Moreover, borrowers pay the ask interest
rate while lenders only receive the bid
interest rate.
Therefore, in the real markets, it is possible
for the forward exchange rate to fluctuate
within a band of rates without presenting
arbitrage opportunities.Only when the
market forward exchange rate diverges
58
from this band of rates arbitrage exists.
NO ARBITRAGE: CASH - AND - CARRY
TIME
CASH
FUTURES
t
(1) BORROW $A. rD,ASK
(4) SHORT FOREIGN CURRENCY FORWARD
(2) BUY FOREIGN CURRENCY
A/SASK($/FC)
FBID ($/FC)
(3) INVEST IN BONDS
A/S ASK ($/FC)e
DENOMINATED IN THE
rF,BID (T-t)
FOREIGN CURRENCY rF,BID
T
REDEEM THE BONDS
DELIVER THE CURRENCY TO CLOSE THE SHORT POSITION
r
EARN:
A/S ASK ($/FC)e F,BID
PAY BACK THE LOAN
Ae
(T-t)
RECEIVE:
FBID ($/FC)A/S( $/FC)e rFOR (T-t)
rD,ASK (T-t)
IN THE ABSENCE OF ARBITRAGE:
Ae
rD,ASK (T t)
 FBID ($/FC)A/S ASK ($/FC)e
FBID ($/FC)  SASK ($/FC)e
rF,BID (T-t)
(rD,ASK - rF,BID )(T-t)
59
NO ARBITRAGE:
REVERSE CASH - AND - CARRY
TIME
CASH
FUTURES
t
(1) BORROW FCA . rF,ASK
(4) LONG FOREIGN CURRENCY FORWARD FOR
FASK(USD/FC)
(2) EXCHANGE FOR
AS BID ($/FC)e
ASBID (USD/FC)
rD, BID (T - t)
(3) INVEST IN T-BILLS
FOR rD,BID
T
REDEEM THE T-BILLS
EARN
TAKE DELIVERY TO CLOSE THE LONG POSITION
AS BID ($/FC)e
PAY BACK THE LOAN
rD, BID (T - t)
Ae
RECEIVE in foreign currency, the amount:
r
rF,ASK (T-t)
IN THE ABSENCE OF ARBITRAGE:
AS BID ($/FC)e D,BID
FASK ($/FC)
r
D, BID
rF,ASK (T- t)  AS BID ($/FC)e
Ae
FASK ($/FC)
FASK ($/FC)  SBID ($/FC)e
( T - t)
( T - t)
(rD, BID rF,ASK )( T-t)
60
From Cash and Carry:
FBID ($/D)  SASK ($/D)e
(1)
(rD,ASK - rF,BID )(T- t)
From reverse cash and Carry
(2)
(3)
FASK ($/D)  SBID ($/D)e
(rD,BID rF,ASK )( T- t)
And FASK($/D) > FBID($/D) Always!
Notice that
The
Define:
RHS(1) > RHS(2)
RHS(1)  BU
RHS(2)  BL
61
F($/D)
FASK
FASK($/D) > FBID($/D).
BU
BU
FBID ($/D)  SASK ($/D)e
(rD,ASK - rF,BID )(T - t)
BL
BL
FBID
FASK ($/D)  SBID ($/D)e
(rD,BID rF,ASK )( T- t)
CONCLUSION:
Arbitrage exists only if both ask and bid futures prices are
above BU, or both are below BL.
62
A numerical example:
Given the following exchange rates:
Spot
S(USD/NZ)
Forward
F(USD/NZ)
Interest rates
r(NZ)
r(US)
ASK
0.4438
0.4480
6.000% 10.8125%
BID
0.4428
0.4450
5.875% 10.6875%
Clearly, F(ask) > F(bid).
(USD0.4480NZ > USD0.4450/NZ)
We will now check whether or not there exists an opportunity
for arbitrage profits. This will require comparing these
forward exchange rates to: BU and BL
63
Inequality (1):
FBID (USD/NZ)
 SASK (USD/NZ)e
(rUS,ASK - rNZ,BID )(T- t)
0.4450 < (0.4438)e(0.108125 – 0.05875)/12 = 0.4456 = BU
Inequality (2):
FASK (USD/NZ)  SBID (USD/NZ)e
(rUS,BID rNZ,ASK )( T- t)
0.4480 > (0.4428)e(0.106875 – 0.06000)/12 = 0.4445 = BL
No arbitrage.
Lets see the graph
64
F
FASK = 0.4480
0.4456
BU
Clearly:
FASK($/FC) > FBID($/FC).
BU
FBID = 0.4450
FBID (USD/NZ)  0.4456
BL
0.4445
BL
FASK (USD/NZ)  0.4445
An example of arbitrage:
FBID = 0.4465
FASK = 0.4480
65