* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download AVL_final
Survey
Document related concepts
Transcript
AVL Trees
Amanuel Lemma
CS252 Algoithms
Dec. 14, 2000
The Basics
Why do operations on ordinary binary search trees
take time as much as O(n)?
–
Each operation takes time proportional to the height
of the tree O(h) which is n in the worst case( for
skewed (unbalanced trees).
So the idea here is to improve running times by
keeping the height with in a certain bound.
AVL trees are ‘balanced’ binary search trees with the
following height balance property :
–
For every internal node v of an AVL tree, the heights
of the children of v can differ by at most one.
Central Theme
Claim : The height balance property gives us the
following result :
•
The height of an AVL tree storing n keys is
at most 1.44 (log n).
Justification: Instead of finding the max height h
directly, we can first determine the minimum
number of internal nodes that an AVL tree of
height h can have and then deduce the
height.
Min-number of Nodes
Let min # of internal nodes at height h be n(h) , then
n(h) = n(h-1) + n(h-2) + 1 where n(1) = 1 and n(2) = 2
This is a fibonacci progression which is exponential in h.
n(h) + 1 5 [(1+ 5) / 2 ] h+3
h 1.44 (log n(h))
Implementation
In addition to implementing the basic binary search tree
we need to store additional information at each internal
node of the AVL tree : balance factor of the node,
bal (v) = height (v.rightChild) – height(v.leftChild)
If we are to maintain an AVL tree, the balance factor of
each internal node must either be –1, 0, or 1. If this rule is
violated, we need to restructure the tree so as to maintain
the height. Obviously, operations such as insert() and
remove() will affect the balance factor of nodes.
Restructuring is done through rotation routines.
Insertion
First part involves the same method of insertion into an
ordinary BST. Secondly, we have to update the balance
factor of the ancestors of the inserted node. Third we
restructure the tree through rotations.
Fortunately there is only one case that causes a
problem : If we insert in an already one higher
subtree then the balance factor will become 2 (right
high) or -2(left high).
This is fixed by performing one rotation of the nodes
which restores balance not only locally but also
globally. So in the case of insertion one rotation
suffices.
Example of an Insert
Example : if we perform insert(32) in the subtree on the
left, the subtree rooted at (40) becomes unbalance
(bal= -2) and a rotation based on inorder traversal
(32->35->40) fixes the problem
Analysis of Insertion
Steps in insertion :
find where to insert + insert + one rotation
Since we have to go down from the root to some
external node when finding the place to insert the key
find() takes O(log n). (height of AVL = 1.44 log n)
Both insert and rotation involve a constant number of
pointer assignments—O(1).
Therefore : O(log n) + O(1) + O(1)
Insert () is O(log n)
Rotations
Rotations involves re-assigning a constant number of
pointers depending on the inorder traversal of the
subtree so as to restore the height balance property. So
each rotation takes constant time O(1).
There are two types :
Single Rotations : reassign at most 6 pointers
Double Rotations: reassign at most 10 pointers
(assuming the tree is doubly linked)
Rotations have 2 properties: (1) the in order visit of the
elements remains the same after the rotation as before
and (2) the overall height of the tree is the same after the
rotation
Algorithm for Rotation
This algorithm combines single and double
rotation into one routine. Another possibility is
to have separate routines for both. (e.g. LEDA)
Node x , y = x.parent , z = y.parent
Algorithm restructure(x) {
1) Let (a,b,c) be a in-order listing of the nodes x, y, and z
and (T0,T1,T2,T3) be in-order listing of the of the four
subtrees of x,y, z.
2) Replace the subtrees rooted at z with sub tree of b.
3) Let a be the left child of b and let T0 and T1 be the left
and right subtrees of a, respectively.
4) Let c be the right child of b and let T2and T3 be the left
and right subtrees of c respectively.
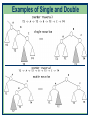
Examples of Single and Double
Remove
Remove operations also involve the same
rotation techniques but are more complicated
than insert for the following reasons:
–
–
–
Can remove from anywhere in tree, possibly
creating holes in the tree. (As in ordinary BST, we
deal with this by replacing it with the key that comes
before it in an inorder traversal of the tree).
From the deleted node to the root of the tree there
can be at most one unbalanced node.
Local restructuring of that node doesn’t have
global effect. So we have to go up to all the
ancestors (up to the root) of the node, updating
balance factor and doing rotations when
necessary.
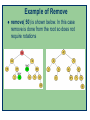
Example of Remove
remove( 50) is shown below. In this case
remove is done from the root so does not
require rotations
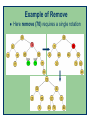
Example of Remove
Here remove (70) requires a single rotation
Analysis of Remove
Remove involves the following operations and
worst case times:
Find + replace with
+
in-order previous
restructure all the way
up to the root
As before all operations done are proportional
to the height of the tree which is 1.44log n for
an AVL tree.
So Find traverses all the way to an external
node from the root in worst case O(log n)
Replace can be shown to take 1/2(1.44log n)
on average but O(log n) in the worst case
Analysis of Remove cont.
There could be at most O(log n) ancestors of a
node and so the heights and balance factors of at
most O(log n) nodes are affected. Since rotations
(single restructure operations) can be done in O(1)
time, the height balance property can be
maintained in O(log n) time.
Remove(total) = O(log n) + O(log n) + O(log n)
So remove takes O(log n) time
LEDA implementation
AVL trees in LEDA are implemented as an
instance of the dictionary ADT. They are leaf
oriented (data is stored only in the leaves) and
doubly linked. They can also be initialized as
an instance of binary trees.
At each node the balance factor is stored.
AVL implementation also includes functions
rotation(u,w,dir) and double_rotation(u,w,x,dir)
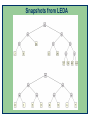
Snapshots from LEDA
Experimenting with LEDA
unsorted entries (chosen at random)
Size
104
105
106
Tree
Type
Insert
time
Look-up Delete
time
Time
AVL
0.0500
0.0200
0.0400 0.1100
BST
0.0400
0.0200
0.0300 0.0900
AVL
0.8900
0.6400
0.9500 2.4800
BST
1.0400
0.7900
0.9500 2.7800
AVL
21.6100 17.7100 20.850 60.170
BST
17.5800 16.1000 16.770 50.450
All values are CPU time in seconds.
Total
Time
Experimenting continued
sorted entries (1,2,3…10n)
Size
Tree
Type
Insert
time
Look-up
time
Delete
Time
Total
Time
104
AVL
BST
0.0500
3.9900
0.0200
3.9700
0.0300
0.0200
0.1000
7.9800
105
AVL
BST
0.6100
-
0.3500
-
0.4500
-
1.4100
-
106
AVL
BST
5.7300
-
4.2400
-
4.9800
-
14.950
-
‘-’ indicates the program stalled
Conclusion
As can be seen from the tables for the case
where the data is chosen at random, ordinary
BST performs somewhat better because of the
overhead of rotation operations in AVL trees.
When the entries are already sorted, which
happens often enough in the real world, the
BST reduces to a linear structure and thus
takes time O(n) per operation while AVL
maintain O(log n) time as can be inferred from
the results.
So dictionary implementations depending on
the ‘expected’ data should use AVL trees.
References
Texts:
Goodrich, Michael and Tamassia, Roberto :
Data Structures and Algorithms in Java.
Kruse, Robert L. : Data Structures & Program
Design.
Applets:
http://www.seanet.com/users/arsen/avltree.html
http://chaos.iu.hioslo.no/~kjenslj/java/applets/latest
/applet.html
Others:
http://www.cs.bgu.ac.il/~cgproj/LEDA/dictionary.html