* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download E-Modul
Hydraulic jumps in rectangular channels wikipedia , lookup
Water metering wikipedia , lookup
Airy wave theory wikipedia , lookup
Lift (force) wikipedia , lookup
Wind-turbine aerodynamics wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Lattice Boltzmann methods wikipedia , lookup
Hemodynamics wikipedia , lookup
Sir George Stokes, 1st Baronet wikipedia , lookup
Boundary layer wikipedia , lookup
Accretion disk wikipedia , lookup
Hemorheology wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Flow measurement wikipedia , lookup
Compressible flow wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Flow conditioning wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Aerodynamics wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Reynolds number wikipedia , lookup
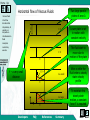
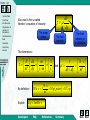
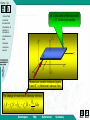
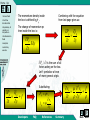
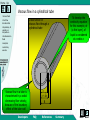
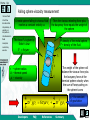
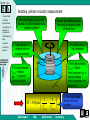
Viscosity Select one subject!! Forfatter Fornavn Etternavn Institusjon Viscous Fluids Fluid Flow Characteristics Dependency of Viscosity on Temperature Non-Newtonian Fluids Examples Laboratory exercise Viscometer Home Up Section 1: Viscous Fluids -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids Horizontal flow of viscous fluids Continuity equation for viscous flow -Examples -Laboratory exercise Select one subject Viscous flow through a porous medium made up of a bundle of identical tubes Viscous flow in a cylindrical tube Exercise: capillary tube viscosity measurement Developers FAQ References Summary Back Next Home Up Horizontal flow of Viscous Fluids Two large parallel plates of area A -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature Y t<0 -Non-Newtonian fluids Lower plate is set in motion with constant velocity -Examples -Laboratory exercise t=0 The fluid start to move due to motion of the plate t is small After a while the fluid enter a steady state velocity profile t is large To maintain this steady state motion, a constant force F is required V v x y, t Y – a very small distance V vx y y x Developers FAQ V References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics The force may be expressed: -Dependency of viscosity on temperature F V A Y -Non-Newtonian fluids -Examples -Laboratory exercise The force F per unit area A is proportional to the velocity V in the distance Y; the constant of proportionally is called the viscosity of the fluid. Developers FAQ References F Y A V Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature Also used is the so called Newton`s equation of viscosity: The shear stress -Non-Newtonian fluids -Examples -Laboratory exercise dv x dy The fluid velocity in x- direction The fluid viscosity The dimensions: N dv m 1 2 , m dy s m s By definition: Explicit: Developers 1Pa s 1 And N s 2 dv / dy m N s 3 10 p ( poise ) 10 cp. 2 m 1cp 1mPa s FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise Typical values of viscosity of some fluids: Temperature Celsius Viscosity Castor Oil, Poise[p] Viscosity Water, centiPoise[cp] Viscosity Air, Micro Poise[ p] 0 53,00 1,792 171 20 9,86 1,005 181 40 2,31 0,656 190 60 0,80 0,469 200 80 0,30 0,357 209 100 0,17 0,284 218 Developers FAQ References Summary Back Next Home Up Continuity equation for viscous flow -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature The flow will have the biggest velocity at the top (the surface ) A liquid is flowing in a open channel -Non-Newtonian fluids -Examples -Laboratory exercise y y X Vx y Fluid flows in an open channel A graphic presentation of this phenomena is shown here The flow velocity will approximately be zero at the bottom, due to retardation when liquid molecules colliding with the non-moving bottom Developers FAQ References Summary Back Next Home Up -Viscous fluids Jp – is often characterised as the momentum intensity or as the shear stress, The unit : 2 -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids N / m Transferred momentum pr. time pr. area -Examples -Laboratory exercise vx jp y Viscosity is here defined as s proportionality constant, similar to what was done in the case of defining absolute permeability Developers FAQ References The change in fluid flow velocity pr. distance between the two layers Summary Back Next Home Up dy is the width of the box and S = S` is the cross-section -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids j`p y -Examples -Laboratory exercise vx S` S z x jp Momentum transfer between layers S and S` in Newtonian viscous flow The change of momentum intensity the box: j p S jp S j p jp S Developers j p y Sdy FAQ References Summary Back Next Home Up The momentum density inside the box is defined by P . -Viscous fluids -Fluid flow characteristics Combining with the equation from last page gives us: The change of momentum pr. time inside the box is : -Dependency of viscosity on temperature -Non-Newtonian fluids P -Examples t -Laboratory exercise P t Sdy j p y P / t is the sum of all forces acting on the box. Let f symbolise a force of more general origin. P t j p y vx 2vx f 2 t y Substituting: P v x v j x y f Developers FAQ References Summary Back Next Home Up Viscous flow in a cylindrical tube -Viscous fluids To develop the continuity equation for this example, dr (a thin layer), of liquid is considered at a radius r. Cross-section of viscous flow through a cylindrical tube -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise s` r r + dr R Viscous flow in a tube is characterised by a radial decreasing flow velocity, because of the boundary effect of the tube wall Developers s FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids The momentum flux through the cylindrical volume: j p jp j p S jp S j p 2rl jp 2 r dr l 2rdrl r r -Examples -Laboratory exercise Here the flux area S is varying and S S . Defining the change in the momentum density inside the cylindrical volume, as P , the general equation for laminar flow is: t 2rdrl jp is redefined according to the geometric conditions in this example: Developers j p j p P f t r r The minus sign show that the flow velocity vx is decreasing when the radius r is increasing v x j p r FAQ The momentum intensity References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids The continuity equation for viscous flow in a cylindrical tube is: v 2v 1 v f 2 t r r r This is under stationary conditions. -Examples -Laboratory exercise At a constant pressure drop p along the tube, no velocity variation is observed v / t 0. 2v 1 v f 0 2 r r r v f r r r r Developers FAQ References Summary Back Next Home Up -Viscous fluids The general solution of the previous equation, found by integrating twice, is: -Fluid flow characteristics -Dependency of viscosity on temperature v -Non-Newtonian fluids 1 f 2 r C1 ln r C2 4 The general constants are found by considering the boundary conditions. For this example the flow is directed along the x-axis -Examples -Laboratory exercise 1. 2. Since the maximum flow velocity, vx(r=0) in the centre of the tube is less then infinity; C1=0 Since the flow velocity is zero along the tube C2 1 / 4( f / ) R 2 wall; vx(r=R)=0 and The solution is then: 1 2 2 f v R r 4 Developers FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics If the outer force, driving the liquid through the tube is the pressure drop p along a tube length l then f p / l and: -Dependency of viscosity on temperature -Non-Newtonian fluids v -Examples Defines a the laminar viscous flow pattern 1 p R2 r 2 4 l -Laboratory exercise R VX -R This flow velocity profile in the tube is given by the formula above. Developers Velocity profile in cylindrical tube flow FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise Viscous flow through a porous medium made up of a bundle of identical tubes The incremental flow rate through a fraction of the cross-section of a capillary tube can be expressed: 2r 2 2 p dq(r ) v(r ) 2r dr R r dr 4 l The total flow rate can be found by integration: 4 dq p R p 2 2 q dr R r dr dr 2l 0 8 l 0 R R For the sake of convenience we may present the last equation in the following form: R 2 p qA 8 l Developers FAQ This is also known as the Poiseuille`s equation, where A is the cross-section of the capillary tube References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise Considering a porous medium as a bundle of identical capillary tubes, the total flow qp through the medium is: Ri2 p k p q p qi Ai A 8 l l i i Where Ai Ri2 is the capillary tube cross-section and A is the crosssection of the porous medium. From the equation above the permeability of the medium where n m capillary tubes are packed together is found: 2 R k R2 32 8 Where the porosity of the bundle of capillary tubes is given by: /4 Developers FAQ References Summary Back Next Home Up Exercise: Capillary tube viscosity measurement -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature Fluid viscosity may also be estimated by the measuring the volume of fluid flowing through a capillary tube pr. time (as the figure below). Rewriting the Poiseuille`s equation an expression for the dynamic fluid viscosity is 4 written: -Non-Newtonian fluids R p t 8 -Examples l V -Laboratory exercise h ~ p L V 2R Developers FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise For horizontal flow through a capillary tube of length L and radius R, the time t it takes to fill a certain volume V is measured. The flow pressure p , is fixed during the process, by maintaining a constant fluid level at a certain elevation above the capillary tube. The accuracy in these measurements is strongly related to the fabrication accuracy of the capillary tubes, as can be seen from the formula above. If the relative uncertainty is considered, 4 R R Which means that if the relative accuracy in the tube-radius is +/- 2-3 %, then the relative accuracy in the viscosity is about +/- 10 %. A small variation in capillary tube fabrication induces large uncertainty in the viscosity measurement. Developers FAQ References Summary Back Next Home Up Section 2: Fluid Flow Characteristics -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature For laminar flow in a cylindrical tube we have derived Poiseuille`s equation: q R 2 p v A 8 l -Non-Newtonian fluids -Examples -Laboratory exercise For turbulent flow in a cylindrical tube, an empirical law, called Fanning`s equation has been found: R p v F l 2 F – the Fanning friction factor Developers FAQ References This factor is dependent of the tube surface roughness, but also on the flow regime established in the tube Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise The flow regime is correlated to the Reynolds number, which characterises the fluid flow in the tube. The Reynolds number, Re, is defined as a dimensionless number balancing the turbulent and the viscous (laminar) flow [ p / l T / p / l L ]. 2R is the spatial dimension where the flow 2 Rv occur – the diameter of a capillary tube or Re width of an open channel. v – the average flow velocity – density – the fluid viscosity From experimental studies an upper limit for laminar flow has been defined at a Reynolds number; Re =2000. Above this number, turbulent flow will dominate. (This limit is not absolute and may therefore change somewhat depending on the experimental conditions.) Developers FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature In the case of porous flow, the velocity v in the previous equation should be the pore flow velocity, where v pore q /(A(1 S or )) and R is the pore radius. The Reynolds number for flow in a porous medium is: -Non-Newtonian fluids Re -Examples -Laboratory exercise 2v B 1 S or vB- the bulk velocity Typical parameters for laboratory liquid flow experiments: R vB S or pore dimension bulk velocity 10m 10 106 m 1cm / s 0,01m / s 1,0 g / cm3 1000kg / m3 porosity 0,25 1cP 1103 Kg / m s viscosity residual oil saturation 10% 0,1 fluid density Developers FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise Using the previous table we find Reynolds number Re = 1 (ca.), for laboratory core flow, which is far below the limit of turbulent flow. In case of reservoir flow, the ”normal” reservoir flow velocity is ca. 1 foot/day or 3,5m / s , which indicate that turbulent liquid flow under reservoir conditions is not very likely to occur. For gas, turbulent flow may occur if the potentials are steep enough. If the formula for Reynolds number and Poiseuille`s law is compared: Re 2 Rk p l 2 The only fluid dependent parameters are the density and the viscosity Comparing the Reynolds number for typical values of gas and oil : Re gas Re oil ( / 2 ) gas ( / 2 ) oil 0,2 g / cm3 /( 0,02cP) 2 2500 3 2 0,8 g / cm /( 2,0cP) Demonstrates the possibilities for turbulent when gas is flowing in a porous medium Developers FAQ References Summary Back Next Home Up Section 3: Dependency of Viscosity on Temperature -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature The Viscosity of liquids decreases with increasing temperature. For gas it`s the opposite; viscosity increase with increasing temperature. -Non-Newtonian fluids -Examples Viscosity, cp -Laboratory exercise Heavy oil Light oil Temperature, K Developers FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise T 3/ 2 K T C Temperature depending viscosity of gases expressed by the Satterland`s equation: Where K and C are constants depending on the type of gas. Another commonly equation: Where n depends on the type of gas (1 < n < 0,75) Developers FAQ References T 0 T0 Summary n Back Next Home Up Section 4: Non-Newtonian Fluids -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise Viscous-Plastic fluids Bingham (1916) and Shvedov (1889) investigated the rheology of viscousplastic fluids. These fluids also feature elasticity in addition to viscosity. Equation describing viscous-plastic fluids: dv 0 ` , when 0 dy when 0 •Here 0is the breaking shear stress • `is the so-called structural viscosity there is no fluid flow Some oils, drilling mud and cements slurries represent viscous-plastic fluids. Developers FAQ References Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids Pseudo-Plastic fluids Some fluids do not have breaking shear stress but rather, their apparent viscosity depends on a shear rate: -Examples n dv k , n 1 dy -Laboratory exercise Which means that their apparent viscosity decreases when dv/dy grows: dv k dv / dy dy Developers FAQ References n 1 Summary Back Next Home Up Section 5: Examples -Viscous fluids -Fluid flow characteristics 6.2.1 Water viscosity at reservoir conditions -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise 6.2.2 Falling sphere viscosity measurement 6.2.4 Rotating cylinder viscosity measurement Developers FAQ References Summary Back Next Home Up Water viscosity at reservoir conditions -Viscous fluids -Dependency of viscosity on temperature Water viscosity is primarily a function of temperature. Salinity has also a slight influence on w . The pure water viscosity is listed in viscous fluids section. Due to correction foe salinity and reservoir temperature, the normal range of viscosity at reservoir conditions is from 0,2 to 1,0 cP. -Non-Newtonian fluids Correlation for estimation of water viscosity at res. temp. : -Fluid flow characteristics -Examples -Laboratory exercise w 4,33 0,07T 4,73 104 T 2 1,415 106 T 3 1,56 10 9 T 4 Water viscosity is measured in cP and temperature in Fahrenheit At a res. temp. of 110 C (230 F ) , the water viscosity will be: w (4,33 0,07 230 4,73 104 2302 1,415 106 2303 1,56 109 2304 )cP 0,40cP NB! Even if the temperature is above , water 100 C at reservoir condition will still be in a liquid phase since the res. Pressure is quite high as compared to surface condition. Developers FAQ References Summary Back Next Home Up Falling sphere viscosity measurement -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise A metal sphere falling in viscous fluid reaches a constant velocity vs Then the viscous retarding force plus the buoyancy force equals the weight of the sphere –s density of the metal sphere f– density of the fluid The force Fs is given by Stoke`s law: Fs 6rvs t0 h r – sphere radius Vs – thermal speed – viscosity t1 The weight of the sphere will balance the viscous force plus the buoyancy force at the terminal sphere velocity when the sum of forces acting on the sphere is zero 4 3 4 3 r g s 6rvs r g f 3 3 Developers FAQ References Summary g – the constant of gravitation Back Next Home Up -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature Viscosity can be estimated by measuring the falling speed of the metal sphere in a cylindrical tube: ( vs h / t ) 2 2 1 r g (s f ) 9 vs -Non-Newtonian fluids -Examples -Laboratory exercise Alternatively; measuring the time t t1 t0 : C ( s f )t C – characteristic constant, determined through calibration with a fluid of known viscosity Developers FAQ References Summary Back Next Home Up Rotating cylinder viscosity measurement -Viscous fluids Here we will also Look at the motion of a fluid between two coaxial cylinders -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples One cylinder is rotating with an angular velocity -Laboratory exercise The inner cylinder: rinner– Radius – Constant Angular velocity Due to the elastic force (in the fluid) a viscosity shear will exist there The other one is kept constant The outer cylinder: router– Radius Held stationary by a spring balance which measures the torque M h M 1 1 M 4h 2 2 rinner router Developers FAQ References 1 h – the fluid height level on the two cylinders Summary Back Next Home Up -Viscous fluids -Fluid flow characteristics For a certain viscometer, the viscosity as function of angular momentum and angular velocity is: -Dependency of viscosity on temperature C -Non-Newtonian fluids -Examples M -Laboratory exercise C – the characteristic constant for the viscometer Developers FAQ References Summary Back Next Home Up Section 6: Laboratory exercise -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise Developers FAQ References Summary Back Next Home Up Section 6: -Viscous fluids -Fluid flow characteristics -Dependency of viscosity on temperature -Non-Newtonian fluids -Examples -Laboratory exercise Developers FAQ References Summary Back Next