Download one-to-one

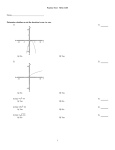
one-to-one
|domain| <= |range|
If the domain and range are defined on the same set then
domain  range
Why?
If a function is one-to-one then for every element in the
domain there is exactly one element in the range. The range
may be bigger. Can you construct a function that is one-toone but not onto?
D = {1,2,3,4}
CoD = {5,6,7,8,9,10}
D x Cod =
{(1,5), (1,6), (1,7), (1,8), (1,9), (1,10),
(2,5), (2,6), (2,7), (2,8), (2,9), (2,10),
(3,5), (3,6), (3,7), (3,8), (3,9), (3,10),
(4,5), (4,6), (4,7), (4,8), (4,9), (4,10)}
Let f = {(1,6),(2,7), 3,8), 4,9)}
Is f onto?
Is f one-to-one
Is f-1 a function?
Is it possible for any function f that f-1 is a function?
Is it possible for any relation r that r-1 is a function?
onto
|domain| >= |range|
If the domain and range are define on the same set then
domain  range
Why?
If a function is onto then for every element in the range
there is at least one element in the domain. The domain may
be bigger. Can you construct a function that is not one-toone but is onto?
D = {1,2,3,4,5,6}
CoD = {7,8,9,10}
D x CoD =
{(1,7), (1,8), (1,9), (1,10),
(2,7), (2,8), (2,9), (2,10),
(3,7), (3,8), (3,9), (3,10),
(4,7), (4,8), (4,9), (4,10),
(5,7), (5,8), (5,9), (5,10),
(6,7), (6,8), (6,9), (6,10)}
Let f = {(1,7), ((2,8), (3,9), (4,10), (5,7), (6,8)}
Is f onto?
Is f one-to-one
Is f-1 a function?
Is it possible for any function f that f-1 is a function?
Is it possible for any relation r that r-1 is a function?
If you think about it for a while you will realize that a
function is onto-one and onto if and only if |domain| =
|range| = |codomain|
From all this we finally get to the rule that says that
function’s inverse is a function if and only if the
function is one-to-one and onto.
That is, f-1 is a function -> f is one-to-one and onto and f
is one-to-one and onto -> f-1 is a function
Suppose f-1 is a function.
Further suppose that for some a and b, f(a) = f(b) = t.
then f-1(t) = f-1f(a) = a and f-1(t) = f-1f(b) = b.
That is f-1(t) = a and f-1(t) = b but f-1 is function.
Therefore, a = b.
Therefore f is one-to-one.
Select any y in f’s codoman.
Since f-1 is function there exists an x in f’s domain such
that f-1(y) = x.
But ff-1(y) = f(x)
That is f(x) = y
That is for any y in f’s codomain there is an x in f’s
domain such that f(x) = y. Therefore f is onto
Therefore f-1 is a function -> f is one-to-one and onto
Suppose f is one-to-one and onto. We want to show that f-1
is a function.
We have to show that if f-1(a) = y and f-1(a) = z then y =
z
Suppose that f-1(a) = y and f-1(a) = z
Then ff-1(a) = a = f(y) and ff-1(a) = a = f(z)
That is a = f(y) and a = f(z)
But f is one-to-one and onto
Therefore y = z
That is, f-1 is a function
It is easy to see all of this from an example
A = {1,2,3}
B = {6,7,8}
A x B =
{(1,6), (1,7), (1,8),
(2,6), (2,7), (2,8),
(3,6), (3,7), (3,8)}
Let f = {(1,6), (2,7), (3,8)}
and
f-1 = {6,1), (7,2), (8,3)}
Is f one-to-one and onto?
Is f-1 a function?
Is f-1 one to one?
From another point of view, a one-to-one and onto function
changes the name of each element in the domain to the name
of an element in the range and the name of every element in
the codomain was once the name of an element in the domain.
pigeonhole principle
The pigeonhole principle is an application of our ideas
about onto function. The size of the domain of an onto
function is always at least as big as the size of its
range. In this case, the domain is the pigeons and the
range is the pigeon holes
Example 45
The domain is the 20 socks
The range is the 10 pairs of socks
Example 46
The domain is the 13 students
The range is the 12 months
Example 47
The domain is the eight people
The range is the 7 days of the week
Example 48
The domain is the number of pairs of initials
The range is the number of students
Example 49
The domain is the people
The range is the number of times they shake hands
Example 50
Try to choose 4 numbers so that the sum of any 2 numbers is
not 7. For each number we choose we must eliminate its pair
in the sum. E.g. If we choose 1 then we cannot choose 6
because 1 + 6 = 7
rule of sum
If a set of objects can be divided into m disjoint subsets
and the ith subset has ni elements , then we have exactly
n1 + n2 + ... + nm elements altogether
rule of product
if an activity can be composed from m different objects, of
which the ith can be chosen in ni ways the we have exactly
n1 x n2 x … nm ways of composing the activity
rule of product examples
If one thing can be done in a given number of different
ways, and then another thing in another given number of
different ways, the number of different ways in which both
things can be done is obtained by multiplying together the
two given numbers.
A selection or combination of any number of articles, means
a group of that number of articles classed together, but
not regarded as having any particular order among
themselves
An arrangement or permutation of any number of articles
means a group of that number of articles, not only classed
together, but regarded as having a particular order among
themselves.
Suppose we have a box containing five upper case letters
and three lower case letters. How many ways can we select
one upper case letter and one lower case letter? How many
ways can we select two upper case letters and two lower
case letters?
5 x 3 = 15 ways to select 1 upper case letter and 1 lower
case letter
(8,2) = 8!/(2! (8–2)!) = 8 x 7 / (2 x 1) = 28
Suppose there is one upper case and one lower case letter.
How many ways can you select and upper case and a lower
case letter?
Suppose there are four paths to the top of the mountain and
back down again. How many ways are there up the mountain
and back down again?
4 x 4 = 16 paths up and back down the mountain
Suppose you had to go down a different way than the way up?
4 ways up
3 ways down
4 x 3 = 12 ways up and back down the mountain
If a penny and a nickel be tossed, in how many ways can
they fall (either heads or tails)?
2 x 2 = 4
Tp,Hn
Hp,Tn
Tp,Hn
Tp,Tn
If two dice be thrown together in how many ways can they
fall (one, two, three, four, five and six)?
6 x 6 = 36
In how many ways can two prizes be given to a class of ten
boys, without giving both to the same boy?
10 ways to give the first prize to a boy
9 ways to give the second prize to a boy
10 x 9 = 90
In how many ways can two prizes be given to a class of ten
boys, it being permitted to give both prizes to the same
boy?
10 ways to give both prizes to the same boy.
90 ways to give both prizes to different boys
Therefore, there are 10 + 90 = 100 ways
10 ways to give the first prize to a boy
10 ways to give the second prize to a boy
10 x 10 = 100
Two persons get into a railway carriage where there are six
vacant sets. In how many different ways can they seat
themselves?
6 ways for the first person to select a seat
5 ways for the second person to select a seat
6 x 5 = 30 ways to select the vacant seats
Suppose there are only 3 seats
(1,2) (2,1) (3,1)
(1,3) (2,3) (3,2)
3 x 2 = 6
In how many ways can we make a two-letter word out of an
alphabet of twenty-six letters, the two letters in the word
being different?
26 x 25 = 650
Suppose you remove the “different letter” restriction. How
many ways?
26 x 26 = 676
In how many ways can we select a consonant and a vowel out
of an alphabet of twenty consonants and six vowels?
20 ways to choose consonant
6 ways to choose vowel
20 x 6 = 120
How many 2 letters “words” that have exactly one consonant
and one vowel?
How many two letter “words” can you form from the set
{a,b}?
ab and ba
You can form 240 “words” from the set of 120 consonants and
vowels.
In how many ways can we make a two-letter word, consisting
of one consonant and one vowel?
240
In how many ways can four letters be put into four
envelopes, one into each?
Repetitions? No!
Does order matter? Maybe!
Suppose order does not matter.
(n,n) = n!/((n-n)!n! = 1
But ordinarily we think that order does matter!
(n)r = n!/(n-r)!
4 x 3 x 2 x 1 = 24
In how many ways can twelve ladies and twelve gentlemen
form themselves into couples for a dance?
Pick Edna! How many ways can Edna select a gentlemen?
12 ways
Pick Sophie. Given that Edna has selected someone, how many
ways can Sophie select someone? 11 ways
How many ways can Edna and Sophie select someone? 12 x 11
Pick Carlotta. How many ways can Carlotta pick someone
given that Edna and Sophie have made their selections? 10
We generalize. The number of ways that the ladies can
select gentlemen is 12 x 11 x 10 ... 3 x 2 x 1 = 12!
In how many different orders can the letters a,b,c,d,e,f be
arranged so as to begin with ab?
(4)4 = 4 x 3 x 2 x 1 = 24
Order matters for words. Consider the set {o,p,s,t}. You
can form the words opts, pots, stop, and pots from this
set.
A table being laid for six persons, in how many ways can
they take their places?
(6)6 = 6 x 5 x 4 x 3 x 2 x 1 = 720
In how many ways can six children form themselves into a
ring?
(6-1)! = 120
How many three-letter words could be made out of an
alphabet of twenty-six letters, not using any letter more
than once?
How many sets of 3 letters are there?
Let’s look at a smaller set. Suppose there are only 5
letters in the alphabet. By our formula, (n,r) = n!/((nr)!r!),
5!/(3!2!) = 10
{a,b,c,d,e}
{a,b,c}, {a,b,d}, {a,b,e}, {a,c,d}, {a,c,e}, {a,d,e}
{b,c,d}, {b,c,e}, {b,d,e}
{c,d,e}
With each of the 10 sets we can generate 6 words:
abc, acb, bac, bca, cab, cba
Therefore we can generate 60 words all together. Back to
the original problem
(26,3) = 26!/(23!3!) = 26 x 25 x 24 /(3 x 2 x 1) = 26 x 25
x 4 = 2600
E.g. {a,b,c} is a set of 3 letters
How many words, not using any letter more than once can you
generate from this set?
3 x 2 x 1 = 6
6 x 2600 = 15600
(26)3 = 26 x 25 x 24 = 15600 also