Download Functions

Functions
Niloufar Shafiei
Application of functions
Applications of functions
Define discrete structures such as sequences
and strings
Represent the time that a computer takes to
solve problems of a given size
Represent the complexity of algorithms
…
1
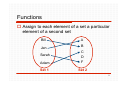
Functions
Assign to each element of a set a particular
element of a second set
Bill
A
Jen
Adam
B
C
D
F
Set 1
Set 2
Sarah
2
Function
Let A and B be nonempty sets.
A function f from A to B is an assignment of exactly
one element of B to each element of A.
If b is the unique element of B assigned by the
function f to the element a of A, we write f(a) = b.
If f is a function from A to B, we write f: A B.
3
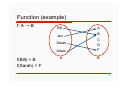
Function (example)
f: A B
Bill
A
Jen
Adam
B
C
D
F
A
B
Sarah
f(Bill) = B
f(Sarah) = F
4
Function and relation
A function from A to B is a relation from A to B
that contains one, and only one, ordered
pair (a,b) for every element a A.
f(a)=b, where (a,b) is the unique ordered pair
in the relation that has a as its first
element.
5
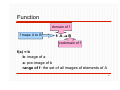
Function
domain of f
f maps A to B
f: A B
codomain of f
f(a) = b
b: image of a
a: pre-image of b
range of f: the set of all images of elements of A
6
Function (example)
f: A B
A
Bill
Jen
Sarah
Adam
Domain of f:
A
B
C
D
F
B
{Bill, Jen, Sarah, Adam}
Codomain of f:
{A,B,C,D,F}
Range of f:
{A,B,F}
7
Function (example)
Let relation R be {(a,1),(g,5),(q,10),(z,22)}.
What is the function that this relation determines?
Solution:
Determine domain, codomain and range of f
domain of f is {a,g,q,z}
codomain of f might be Z+
range of f is {1,5,10,22}
Determine image for each element of the domain
f(a)=1
f(g)=5
f(q)=10
f(z)=22
8
Function (example)
Assume a function f maps any integer x to x+1.
Determine the function?
Solution:
Determine domain, codomain and range of f
domain of f is Z
codomain of f is Z
range of f is Z
Determine image for each element of the domain
f(x)=x+1
9
Functions in programming
The domain and codomain of functions are often
specified in programming language.
Example:
Java:
int f(float x){…}
Pascal:
function f(x: real): integer
Domain of f: R
Codomain of f: Z
10
Equal functions
Assume f and g are two functions.
f and g are equal when they have the same domain,
the same codomain and map each element of
their domain to the same element in codomain.
xdomain f(x)=g(x)
f=g iff they are equal as sets.
11
Equal functions (example)
f: Z R
f(x): x+1
g: Z Z
g(x): x+1
f g
different codomain
f: Z Z
g: Z Z
f=g
f(x): x2 + 2x + 1
g(x): (x+1)2
12
Functions
Let f and g be functions from A to R.
f+g and fg are also functions from A to R.
(f+g)(x) = f(x) + g(x)
(fg)(x) = f(x).g(x)
13
Example
Assume f: R R and g: R R such that
f(x)=x2 and g(x)=x-x2. what are the
functions f+g and fg?
Solution:
(f+g)(x) = x2 + x - x2 = x
(f+g)(x):R R
(fg)(x) = x2(x-x2) = x3-x4
(fg)(x):R R
14
Image of a set
Assume f: AB and SA.
The image of S under the function f, denoted by
f(S), consists of the images of the elements of S.
f(S) = {t | sS ( t=f(s) ) }
= {f(s) | sS}
f(S) B
15
Image of a set (example)
Assume f: ZZ and f(x) = x2-1
Let S be {0,1,2}.
What is the image of S under function f?
Solution:
f(S) = {f(0), f(1), f(2)}
= {-1,0,3}
16
One-to-one function
Assume f: AB.
f is one-to-one or injective, if and only if
a,bA ((f(a)=f(b)) (a=b)).
f is one-to-one if and only if
a,bA ((a b) (f(a) f (b))).
f never assigns the same value to two different
domain elements.
17
One-to-one function (example)
f: AB
Is the function f
one-to-one?
A
Bill
Jen
Sarah
Adam
A
B
C
D
F
B
Solution:
f is not one-to-one.
Because f(Bill) = f(Adam).
18
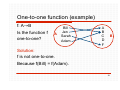
One-to-one function (example)
f: AB
Is the function f
one-to-one?
A
Bill
Jen
Sarah
Adam
A
B
C
D
F
B
Solution:
f is one-to-one.
Because a,bA ((a b) (f(a) f (b)))..
19
One-to-one function (example)
Is the function f(x)=x2 from the set of integers
to the set of integers one-to-one?
Solution:
f is not one-to-one.
Because f(1) = f(-1), but 1 -1.
20
One-to-one function (example)
Is the function f(x)=x+1 from the set of real
numbers to the set of real numbers one-toone?
Solution:
f is one-to-one.
Because x+1 y+1 when x y.
21
One-to-one function (example)
Does f and g are one-to-one imply f+g is one-to-one?
Solution:
Try to find counterexample
f(0)=0 f(1)=1 f(2)=-1
(f is one-to-one)
g(0)=0 g(1)=-1 g(2)=1
(g is one-to-one)
f+g(0)=0 f+g(1)=0 f+g(2)=0
So, f+g is not one-to-one.
22
Onto functions
Assume f: AB.
f is called onto, or surjective, if and only if for
bB aA (f(a)=b).
Every element of the codomain is the image of some
element of the domain.
The range and codomain are equal.
23
Onto functions (example)
f:AB
Is function f onto?
A
a
b
c
d
1
2
3
B
Solution:
f is onto.
Because the range and codomain (={1,2,3}) are
equal.
Every element in codomain is an image of some
element in domain.
24
Onto functions (example)
f:AB
Is function f onto?
A
a
b
c
d
Solution:
f is not onto.
Because the range (={1,2,3}) and codomain
(={1,2,3,4}) are not equal.
1
2
3
4
B
25
Onto functions (example)
Assume f: ZZ.
Is function f(x)=x2 onto?
Solution:
f is not onto.
Because there is no integer x with x2 = -1.
(Negative integers are not in the range of f but
the codomain contains all integers)
26
Onto functions (example)
Assume f: ZZ.
Is function f(x)=x+1 onto?
Solution: (backward reasoning)
f is onto, because
Let yZ, x (namely x=y-1).
y x (x=y-1)
y x (x+1=y)
y x (f(x)=y)
27
Bijection function
The function f is a bijection, or a one-to-one
correspondence, if it is both one-to-one
and onto.
a,bA ((f(a)=f(b)) (a=b)) bB aA (f(a)=b)
28
Bijection function (example)
Let A be a set. The identity function on A is
I:AA where I(x)=x.
Is the function I bijection?
Solution:
Check if I is one-to-one.
a,bA ((I(a)=I(b)) (a=b))
a,bA ((a=b) (a=b))
So, function I is one-to-one
29
Bijection function (example)
Let A be a set. The identity function on A is
I:AA where I(x)=x.
Is the function I bijection?
Solution:
Check if I is onto.
The range(=A) and codomain(=A) are
equal.
So, function I is onto.
Thus, function I is bijection.
30
Increasing and decreasing functions
Assume f: AB, AR and BR.
f is increasing if a,bA ((a<b) (f(a)f(b)).
f is strictly increasing if a,bA ((a<b) (f(a)<f(b)).
f is decreasing if a,bA ((a<b) (f(a)f(b)).
f is strictly decreasing if a,bA ((a<b) (f(a)>f(b)).
Strictly decreasing and strictly increasing functions are one-to-one.
31
Increasing and decreasing functions
(example)
Is the function f(x)=x+1 from the set of real
numbers to the set of real numbers strictly
increasing?
Solution:
Assume x,yR.
If x<y, then x+1<y+1.
So, f is strictly increasing.
32
Increasing and decreasing functions
(example)
Show that Strictly decreasing functions are
one-to-one.
Solution:
Assume f:AB is strictly decreasing.
a,bA ((a<b) (f(a)>f(b))
a,bA ((a b) (f(a) f (b))
So, f is one-to-one.
33
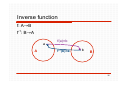
Inverse function
Let f be a bijective function from A to B.
The inverse function of f, denoted by f-1, is the
function that assigns to an element bB the
unique element aA such that f(a)=b.
when f(a) = b, f -1(b) = a.
f -1 : BA
A bijective function is called invertible.
The function is not invertible if it is not bijection.
34
Inverse function
f: AB
f-1: BA
a
A
f(a)=b
f-1(b)=a
b
B
35
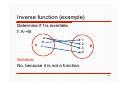
Inverse function (example)
Determine if f is invertible.
f: AB
A
a
b
c
d
1
2
3
B
Solution:
No, because it is not one-to-one.
36
Inverse function (example)
Show that f-1 is always one-to-one.
Solution:
f:AB
f-1:BA
f(a) = b then f -1(b) = a
Since f is a function, f assigns exactly one element of
B to each element of A.
If f(a)=b and f(a)=b’, then b=b’.
b,b’B ((f-1(b)=f-1(b’)) (b=b’))
So, f-1 is on-to-one.
37
Inverse function (example)
Determine if f is invertible.
f: AB
A
a
b
c
1
2
3
4
B
Solution:
No, because it is not a function.
38
Inverse function (example)
Determine if f is invertible.
f: AB
A
a
b
c
d
1
2
3
4
B
Solution:
No, because it is neither one-to-one nor onto.
39
Inverse function (example)
Determine if f is invertible. If it is invertible, what is its
inverse function.
f: AB
A
a
b
c
1
2
3
B
Solution:
Yes, because it is one-to-one and onto.
f-1: BA
f-1(1)=b
f-1(2)=a
f-1(3)=c
40
Inverse function (example)
Assume function f is from nonnegative real numbers to
nonnegative real numbers, where f(x)=x2.
Determine if f is invertible. If it is invertible, what is its inverse
function.
Solution:
Check if f is one-to-one
Assume x and y are nonnegative real numbers.
x,y ((f(x)=f(y)) (x=y))
(one-to-one definition)
x2 = y2
x2 - y2 = 0
(x+y)(x-y)=0
So, x=y or x=-y.
Since x and y are nonnegative real numbers, x=y.
So, function f is one-to-one.
(or use the fact that it is strictly increasing.)
41
Inverse function (example)
Assume function f is from nonnegative real numbers to
nonnegative real numbers, where f(x)=x2.
Determine if f is invertible. If it is invertible, what is its inverse
function.
Solution:
Check if f is onto
Assume x and y are nonnegative real numbers.
y x (f(x)=y)
(definition of onto)
x2 = y
x = y
Since for every y, there exists a nonnegative real number
x, then f(x) is onto.
Thus, f is bijection and it is invertible
42
Inverse function (example)
Assume function f is from nonnegative real numbers to
nonnegative real numbers, where f(x)=x2.
Determine if f is invertible. If it is invertible, what is its inverse
function.
Solution:
Find f-1
f(x) = x2
f-1 (x) = x
f-1 is from nonnegative real numbers to nonnegative real
numbers
43
Inverse function (example)
Assume f:AB and f is invertible. Determine (f-1)-1.
Solution:
f-1 :BA
If f(a)=b, then f-1(b)=a.
(f-1)-1 :AB
If f-1(b)=a, then (f-1)-1(a) =b.
So, (f-1)-1 = f.
44
Composition of functions
Assume g:AB and f:BC.
The composition of g and f, denoted by (f º g),
is defined by (f º g)(x) = f(g(x)).
(f º g)(a)=c
a
A
g(a)=b
b
c
B
f(b)=c
C
45
Composition of functions (example)
Assume A={a,b,c}, B={1,2,3} and
g:AA where g(a)=b, g(b)=c and g(c)=a, and
f:AB where f(a)=3, f(b)=2 and f(c)=1.
What is (f º g)(x)?
Solution:
(f º g):AB
(f º g)(a) = f(g(a)) = f(b) = 2
(f º g)(b) = f(g(b)) = f(c) = 1
(f º g)(c) = f(g(c)) = f(a) = 3
46
Composition of functions (example)
Assume g:ZZ where g(x)=3x+2, and f:ZZ where f(x)=2x+3.
Determine if (f º g) = (gº f).
Solution:
(f º g):ZZ
(f º g)(x) = f(g(x))
= f(3x+2)
= 2(3x+2) + 3
= 6x + 7
(g º f):ZZ
(g º f)(x) = g(f(x)) = g(2x+3) = 3(2x+3) + 2 = 6x + 11
So, (f º g) and (gº f) are not equal.
47
Composition of functions (example)
Assume f:AB and f is a bijection. Determine (f º f-1) and (f-1 º f).
Solution:
f:AB
f-1:BA
If f(a) = b, then f-1(b)=a.
f º f-1:BB
(f º f-1)(b) = f(f-1(b))
= f(a)
=b
(f-1 º f):AA
(f-1 º f)(a) = f-1(f(a)) = f-1(b) = a
So, (f º f-1) and (f-1 º f) are identify functions but on different
domains.
48
The graphs of functions (example)
Assume f: ZZ where f(x)= 2x+1. Display the graph of f.(graph
is a pictorial representation of a function.)
Solution:
The graph of f is the set of ordered pairs of the form (x,2x+1).
49
The graphs of functions (example)
Assume f: ZZ where f(x)= x2.
Display the graph of f.
Solution:
The graph of f is the set of ordered pairs of the form (x,x2).
50
Floor and ceiling functions
Floor: RZ
Floor function rounds x down to the closest integer
less than or equal to x and it is denoted by x.
Example:
2.3 = 2
-1/2 = -1
Ceiling: RZ
Ceiling function rounds x up to the closest integer
greater than or equal to x and it is denoted by x.
Example:
2.3 = 3
-1/2 = 0
51
Floor and ceiling functions
(example)
Display the graph of floor function.
Solution:
The graph of f is the set of ordered pairs of the form (x, x).
Floor function is x throughout the interval [x,x+1).
52
Floor and ceiling functions
(example)
Show that x+n is x+n.
Proof:
Assume x = m.
m-1 < x m
n+m-1 < x+n m+n
x+n = m+n
(by definition of ceiling function)
x+n = x+n
53
Floor and ceiling functions
(example)
Show that 2x = x + x+1/2 where x is a real number.
Proof:
Assume x=n+ where n is integer and 0<1.
Case1: 0<1/2
2x = 2n+2
(02<1)
2x = 2n
x+1/2 = n++1/2 (1/2+1/2<1)
x+1/2 = n
x + x+1/2 = n+ + n = n+n = 2n
So, 2x = x + x+1/2.
54
Floor and ceiling functions
(example)
Show that 2x = x + x+1/2 where x is a real number.
Proof:
Assume x=n+ where n is integer and 0<1.
Case2: 1/2<1
2x = 2n+2
= 2n+1+2-1
(02-1<1)
= 2n+1
x+1/2 = n++1/2
= n+1+ -1/2 (0-1/2<1/2)
x+1/2 = n + 1
x + x+1/2 = n+ + n + 1 = n+n+1 = 2n + 1
So, 2x = x + x+1/2.
55
Floor and ceiling functions
(example)
disprove that x+y = x + y where x and y are real
numbers.
Proof:
Find counterexample
x=1/3 and y=2/3
1/3+2/3 = 1 = 1
1/3 + 2/3 = 0 + 0 = 0
56
Recommended exercises
1,7,9,10,15,19,21,25,27,29,34,39,41,61,63,69
57