Download Basic Electrostatics

Basic Electrostatics
From Molecular to Con/nuum Physics I WS 11/12
Emiliano Ippoli/| October, 2011
Wednesday, October 12, 2011
Review
Mathematics
...
Physics
• Basic thermodynamics
• Temperature, ideal gas, kinetic gas theory, laws of thermodynamics
• Statistical thermodynamics
• Canonical ensemble, Boltzmann statistics, partition functions, internal and free energy, entropy
• Basic electrostatics
• Classical mechanics
• Newtonian, Lagrangian, Hamiltonian mechanics
• Quantum mechanics
• Wave mechanics
• Wave function and Born probability interpretation
• Schrödinger equation
• Simple systems for which there is an analytical solution
• Free particle
• Particle in a box, particle on a ring
• Rigid rotator
• Harmonic oscillator
• Basics
• Uncertainty relation
• Operators and expectation values
• Angular momentum
• Hydrogen atom
• Energy values, atomic orbitals
• Electron spin
• Quantum mechanics of several particles (Pauli principle)
• Many electron atoms
• Periodic system: structural principle
• Molecules
• Two-atomic molecules (H2+,H2, X2)
• Many-atomic molecules
Emiliano Ippoliti
Wednesday, October 12, 2011
Chemistry
Informatics
...
...
2
Coulomb’s law
Let us consider two point-like
electric charges q and Q at position
x1 and x2, respectively.
The force on q due to Q is then:

qQ 
FQ→q = k 3 r
r

 
r = r = xq − xQ
1. proportional to the strength of charges;
2. inversely proportional to the square of the separation;
3. directed along the line connecting the charges;
4. repulsive for like charges and attractive for opposite charges.
Emiliano Ippoliti
Wednesday, October 12, 2011
3
Units
In SI units:
1
k=
≈ 9 × 10 9 Nm 2C-2
4πε 0
an electron carries a charge e equal
to 1.6 x 10−19 C
In Gaussian units:
k =1
an electron carries a charge e equal
to 4.803 x 10−10 statcoulomb
1 statcoulomb = 3.3356 10−10 C
Emiliano Ippoliti
Wednesday, October 12, 2011
4
Electric field
Take a very small test charge q (small so that it does not
disturb the charge distribution whose field we're measuring),
and measure the force on the test charge as a function of
position x. Then the electric field is defined as:


F ( x)
E ( x ) = lim
q→0
q

 
Q x
Q ê r
E(x) =
3 =
2
4πε 0 x
4πε 0 r
Emiliano Ippoliti
Wednesday, October 12, 2011
5
Superposition
principle
It is an experimental fact that electrostatics is linear, so that
the electric fields produced by a collection of point charges

{qi} at positions {xi} simply add:


 
1
x − xi
E(x) =
qi   3
∑
4πε 0 i =1 x − xi
N
that can be rewritten as:
 
E(x) =
1
⎡
 ⎤
3
(3) 
d x ′ ⎢ ∑ qiδ ( x ′ − xi ) ⎥
∫
4πε 0
⎣i =1

⎦
ρ ( x′ )
N
Charge density
Emiliano Ippoliti
Wednesday, October 12, 2011
6
 
x − x′
  3
x − x′
Dirac delta function
The Dirac delta function is a mathematically convenient way
of representing singularities such as point charges.
It is really not a function but a “distribution.” However, we will
ignore this at this level.
One way of defining the delta function in one dimension is:
⎧ 1/ w
⎪
δ ( x ) = lim ⎨
w→0
⎪ 0
⎩
Emiliano Ippoliti
Wednesday, October 12, 2011
7
if - w / 2 < x < w / 2
otherwise
Dirac delta function
Properties
+∞
1.
∫ δ ( x ) dx = 1.
−∞
+∞
2.
∫ δ ( x − a ) f ( x ) dx = f ( a ).
−∞
+∞
3.
∫ δ ′ ( x − a ) f ( x ) dx = − f ′ ( a ) [ integrate by parts and use 2 ].
−∞
4. Let f ( x ) have simple zeros at { xi } , i.e. f ( x ) ≈ f ′ ( x ) ( x − xi ) for x near xi , then
δ ⎡⎣ f ( x ) ⎤⎦ = ∑
i
1
δ ( x − xi ) .
f ′ ( xi )

5. In three dimensions δ ( x) = δ (x)δ (y)δ (z). This simple formula hold only with
cartesian coordinates.
(d ) 
6. In d dimensions, δ ( x ) has dimensions of L− d .
Emiliano Ippoliti
Wednesday, October 12, 2011
8
Gauss’ law
For a single charge q:

E ⋅ n̂ =
q cosθ
4πε 0 r 2
so that the flux of the electric field through the area
element da is:

E ⋅ n̂ da =
q da cosθ
q
=
dΩ
2
4πε 0
r
4πε 0
Then, integrating over the entire surface:

q
∫ S E ⋅ n̂ da = ε 0
Emiliano Ippoliti
Wednesday, October 12, 2011
9
solid angle subtended by
da (i.e., r2 dΩ = cosθ da)
( ∫
S
dΩ = 4π
)
Differential form of
the Gauss’ law
For a collection of charges {qi} inside the surface:

1
1
∫ S E ⋅ n̂ da = ε 0 ∑i qi = ε 0
∫
V
 3
ρ(x)d x
The divergence theorem states:
∫
S

A ⋅ n̂ da =
∫
V
  3
∇⋅A d x
Then
∫
S
Emiliano Ippoliti
Wednesday, October 12, 2011

E ⋅ n̂ da =
10
  3
1
∫V ∇ ⋅ E d x = ε 0
  ρ
 3
∫V ρ ( x ) d x ⇒ ∇ ⋅ E = ε 0
Electrostatic potential
By using the identity:
 ⎛ 1⎞
ê r
∇⎜ ⎟ = − 2
⎝ r⎠
r
 ⎛ q ⎞
we can write the electric field of a point charge: E = ∇ ⎜
⎝ 4πε 0 r ⎟⎠
and the field of a set of charges:
 1
 

1
E=−
qi ∇   ≡ −∇Φ ( x )
∑
4πε 0 i
x − xi
where Φ is the electrostatic potential:

Φ( x ) =
Emiliano Ippoliti
Wednesday, October 12, 2011
11
1
qi
1
  =
∑
4πε 0 i x − xi
4πε 0
∫

ρ ( x′ ) 3
  d x′
x − xi
Meaning of Φ

If there are no charges at infinity, so that Φ ( ∞ ) = 0, then qΦ ( x )

is the work required to bring a charge q from ∞ to x (the
other charges being held fixed).
More generally, the work to bring q from A to B is
B
 
 
W = − ∫ F ⋅ dl = − ∫ qE ⋅ dl = q ⎡⎣ Φ ( B ) − Φ ( A ) ⎤⎦
B
A
A
The work done depends only on the end points (A, B), not on
the path; hence the net work in going around a closed path is
zero. In this case one says the electric field is conservative.
Emiliano Ippoliti
Wednesday, October 12, 2011
12
Curl of the
electric field
For any smooth function Φ:


∇ × ∇Φ = 0


where the curl ∇ × of a vector V is defined as:
( )
  ⎛ ∂Vz ∂Vy ⎞
⎛ ∂Vy ∂Vx ⎞
⎛ ∂Vx ∂Vz ⎞
∇×V = ⎜
−
ê x + ⎜
−
ê y + ⎜
−
ê z
⎟
⎟
⎟
⎝ ∂z
⎝ ∂y
⎝ ∂x
∂z ⎠
∂x ⎠
∂y ⎠
Therefore
Emiliano Ippoliti
Wednesday, October 12, 2011
 
∇×E =0
13
Stokes’ theorem
From the Stokes’ theorem:
∫
C
 
A ⋅ dl =
∫
S

∇ × A ⋅ n̂ da
where S is any surface bounded by the closed contour C, we
can derive the previous statement that the work in going for
a closed path is zero:
∫
C
Emiliano Ippoliti
Wednesday, October 12, 2011
14
 
E ⋅ dl =
∫
S

∇ × E ⋅ n̂ da = 0
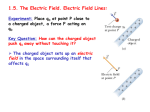
Lines of forces
The lines of force (also called the field lines) provide a
method for graphing the electric field.

• They are everywhere tangent to the electric field E and therefore for
a point charge are tangent to the force exerted by the field on the
particle.
• They begin on positive charges and terminate on negative charges.
• The local density of the field lines is proportional to the strength of
the electric field.
• The electric field lines do not cross (otherwise the field would not
be unique at that point).
The lines of force are not particle trajectories!
The
particle



trajectories are obtained by solving F = ma with F = qE .
Emiliano Ippoliti
Wednesday, October 12, 2011
15
Lines of forces
Examples
1 CHARGE
2 CHARGES
The equipotentials are contours of constant electrostatic
potential. They are analogous to the contours on a
topographic map. They are perpendicular to the lines of
force.
Emiliano Ippoliti
Wednesday, October 12, 2011
16
Dipole
A dipole is a model of two point charges q and -q at positions


x ′and x′′, separated by a infinitesimal displacement
 
d = x ′ − x ′′

The potential in the point P at position x will then be:
  
⎤
1 ⎡ q
q
1 p ⋅ ( x − x′ )

Φ( x ) =
→
⎢  −  
⎥ ⎯d⎯⎯
  3
→0
4πε 0 ⎣ x − x ′
x − x′ + d ⎦
4πε 0 x − x ′


where the dipole moment p = qd.
Emiliano Ippoliti
Wednesday, October 12, 2011
17
Dipole
The electrostatic potential can also be written as

Φ( x ) =
1 p cosθ
2
4πε 0 r
where θ is the angle between the dipole moment and the
observation point P.
The electric field is then:

 
1 3n̂ ( p ⋅ n̂ ) − p
E(x) =
  3
4πε 0
x − x′



where n is the unit vector directed from x′to x.
x
Emiliano Ippoliti
Wednesday, October 12, 2011
18
Poisson equation
Starting from the Coulomb’s law we have derived the two
differential field equations of electrostatics:
 
∇×E =0
 
∇ ⋅ E = ρ / ε0
The most general solution of the first equation can be written:


E = −∇Φ
Inserting it in the second equation, we find that Φ must satisfy:
∇ Φ = −ρ / ε0
2
Poisson equation
In a region of space with no sources (ρ = 0) this reduces to:
∇ Φ=0
2
Emiliano Ippoliti
Wednesday, October 12, 2011
19
Laplace equation
References
1. A. Dorsey. Basic Electrostatics. http://www.phys.ufl.edu/
~dorsey/phy6346-00/lectures/lect01.pdf
2. D.J. Griffiths. Introduction to Electrodynamics. 3th Eds.
Benjamin Cummings, New Jersey, 1999.
3. J.D. Jackson. Classical Electrodynamics. 3th Eds. John Wiley &
Son, New York, 1998.
Emiliano Ippoliti
Wednesday, October 12, 2011
20