* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ch 1 Notes
Cartesian coordinate system wikipedia , lookup
List of regular polytopes and compounds wikipedia , lookup
Tessellation wikipedia , lookup
Analytic geometry wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
History of geometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Perceived visual angle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Integer triangle wikipedia , lookup
Multilateration wikipedia , lookup
Euler angles wikipedia , lookup
Rational trigonometry wikipedia , lookup
Compass-and-straightedge construction wikipedia , lookup
Geometry Definitions, Postulates, and Theorems
Chapter 1: Essentials of Geometry
Section 1.1: Identify Points, Lines, and Planes
Standards: 1.0 Students demonstrate understanding by identifying and giving examples of undefined terms, axioms,
theorems, and inductive and deductive reasoning.
Three Undefined Terms in Geometry: *Point, Line, & Plane. Descriptions are below.
Point –
Line –
Plane –
Collinear –
Ex. Points Q, R, and T are collinear.
Points Q, R, and S are noncollinear.
Coplanar – Points that lie on the same plane.
Ex. Name 3 points that are coplanar
Name 4 points that are noncoplanar
Name 3 collinear points
Segment – Symbolized AB .
(over)
Ray – Symbolized AB.
Opposite Rays –
Intersect –
Ex. Draw a line and a plane that do not intersect.
Ex. Draw 2 lines that intersect and one that does not.
Intersection –
Ex. Draw a line and a plane that intersect. Their intersection forms a
Ex. Draw 2 planes that intersect. Their intersection forms a
Ex. Draw 3 collinear points A, B, C.
Draw D which is noncollinear with A, B and C.
Draw AB and BD .
.
.
Section 1.2: Use Segments and Congruence
Standards: 1.0 Students demonstrate understanding by identifying and giving examples of undefined terms, axioms,
theorems, and inductive and deductive reasoning.
Postulates or Axioms –
Coordinate –
Distance of a segment –
Ruler Postulate –
Between –
***Segment Addition Postulate – IF B is between A and C, THEN AB + BC = AC.
IF AB + BC = AC, THEN B is between A and C.
Ex. Given GK = 24, HJ = 10, GH=HI=IJ,
find HI and IK.
G
H
I
J
K
***Congruent Segments –
Ex. J is between H and K. Solve for x.
HJ = 2x + 5, JK = 3x – 7, KH = 18
Section 1.3: Use Midpoint and Distance Formulas
Standards: Prepare for 7.0 Students prove theorems by using coordinate geometry, including the midpoint of a line
segment, the distance formula, and various forms of equations of lines and circles.
***Midpoint –
Bisects –
***Segment Bisector –
Ex. M is the midpoint of segment GH . Find MH.
G
M
5x – 8
H
3x + 14
Midpoint Formula –
Ex. Find the coordinates of the midpoint of
AB if A(-2,-3) and B(5,-2).
Ex. The midpoint of JK is M(0, ½).
One endpoint is J(2,-2), find K(x,y).
(over)
Distance Formula –
Ex. Given A(3,2) and B(-1,1), find AB.
Ex. Find the distance between B (-1, 1) and C(-2, -1).
Pythagorean Theorem –
c
a
a 2 + b 2 = c2
b
Review: Simplifying Radicals. (Doubles get you out of jail)
Ex.
a)
20
d)
80
b)
c)
60
e)
1050
72
Section 1.4: Measure and Classify Angles
Standards: 1.0 Students demonstrate understanding by identifying and giving examples of undefined terms, axioms,
theorems, and inductive and deductive reasoning.
Angle –
Sides –
Vertex –
An angle is symbolized by three letters, where the center letter is the vertex.
Measure of an angle –
Protractor Postulate –
Acute Angle –
***Right Angle –
Obtuse Angle –
(over)
***Straight Angle –
***Angle Addition Postulate –
***Congruent Angles –
Ex. Find mSTV .
S
Ex. Given mMNP 70 ,
find mMNO .
P
Ex. Find the missing angle.
U
O
30°
20°
80°
120°
N
?
T °
V
M
***Angle Bisector –
Ex. CD bisects ACB . Given mACD ( x 10) and mBCD (3 x 20) , solve for x and find
mACB .
Section 1.5: Describe Angle Pair Relationships
Standards: 13.0 Students prove relationships between angles in polygons by using properties of complementary,
supplementary, vertical, and exterior angles.
***Complementary Angles –
Complement –
Ex. A and B are complementary. Given mA (5 x 8) and mB ( x 4) , find mAand mB .
***Supplementary Angles –
Supplement –
Ex. A and B are supplementary. Given mA (3x) and mB ( x 8) , find mAand mB .
Adjacent Angles –
***Linear Pair –
1
4
3
2
(over)
***Vertical Angles –
1
4
3
2
Ex. True or False.
a) 1 and 2 are a linear pair.
2
b) 4 and 5 are a linear pair.
1
c) 5 and 3 are vertical angles.
5
3
4
d) 1 and 3 are vertical angles.
e) If m3 40 , find: m1
m2
m4
m5
Ex. Given m1 (4x + 15)°, m2 (5x + 30)°, m3 (3y – 15)°, and m4 (3y+15)°, find x and y
and the measure of each angle.
1
4
2
3
Section 1.6: Classify Polygons
Standards: 12.0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to
classify figures and solve problems.
Polygon – A plane figure that:
1.
2.
Sides –
Vertex –
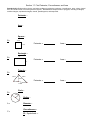
Ex. Is it a polygon? (write yes or no)
a)
b)
c)
d)
e)
Convex –
ENGLISH TRANSLATION – A polygon without any dents!
Nonconvex (or concave) –
ENGLISH TRANSLATION – A polygon with a dent, or two, or three, etc.!
Polygons are named by the number of sides they have.
Number of sides
3
4
5
6
7
8
9
10
11
12
n
Type of polygons
triangle
quadrilateral
pentagon
hexagon
heptagon or septagon
octagon
nonagon
decagon
hendecagon
dodecagon
n-gon ("n" sides, where n is a variable)
(over)
Regular –
1.
2.
Diagonal –
Ex. Draw a regular hexagon. Draw all the diagonals.
Ex. Find the value of x in the regular polygon.
x2 + 3x – 4
x2 – x
Section 1.7: Find Perimeter, Circumference, and Area
Standards: 8.0 Students know, derive, and solve problems involving the perimeter, circumference, area, volume, lateral
area, and surface area of common geometric figures. 10.0 Students compute areas of polygons, including rectangles,
scalene triangles, equilateral triangles, rhombi, parallelograms, and trapezoids.
Perimeter –
Area –
Square –
Ex.
3 cm
Perimeter =
Area =
Perimeter =
Area =
Perimeter =
Area =
3 cm
Rectangle –
8”
Ex.
5”
Triangle –
Ex.
8mm
9mm
6mm
11mm
Circle –
Ex.
4cm
Radius –
A=
Diameter –
Circumference –
C=
Pi – Symbolized .
(over)
Ex. Find the area and perimeter of the triangle defined by H(-2,2), J(3,-1) and K(-2,-4).
y
x
Ex. A rectangle has an area of 15.4 ft2. It’s length is 7 ft. What is the width?