* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 4.6 Triangle Congruence CPCTC
Lie sphere geometry wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Technical drawing wikipedia , lookup
Analytic geometry wikipedia , lookup
Algebraic geometry wikipedia , lookup
Shape of the universe wikipedia , lookup
Trigonometric functions wikipedia , lookup
Cartan connection wikipedia , lookup
Rational trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
History of trigonometry wikipedia , lookup
Geometrization conjecture wikipedia , lookup
Line (geometry) wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
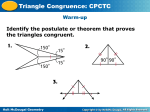
4-6 Triangle Congruence: CPCTC Toolbox Pg. 263 (4; 7-11;17-18; 24 why4) Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC Essential Question How do you use CPCTC to prove parts of triangles are congruent? Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC CPCTC is an abbreviation for the phrase “Corresponding Parts of Congruent Triangles are Congruent.” It can be used as a justification in a proof after you have proven two triangles congruent. Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC Remember! SSS, SAS, ASA, AAS, and HL use corresponding parts to prove triangles congruent. CPCTC uses congruent triangles to prove corresponding parts congruent. Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC Example 1: Engineering Application A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC Example 2: Proving Corresponding Parts Congruent Given: YW bisects XZ, XY YZ. Prove: XYW ZYW Z Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC Example 2 Continued Statement 1) YW bisects XZ 2) XW ZW 3) XY YZ 4) YW WY 5) XYW ZYW 6) XYW ZYW Holt McDougal Geometry Reason 1) Given 2) Dfn of bisector 3) Given 4) Reflexive prop 5) SSS 6) CPCTC 4-6 Triangle Congruence: CPCTC Helpful Hint Work backward when planning a proof. To show that ED || GF, look for a pair of angles that are congruent. Then look for triangles that contain these angles. Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC Example 3: Using CPCTC in a Proof Given: NO || MP, N P Prove: MN || OP Holt McDougal Geometry 4-6 Triangle Congruence: CPCTC Example 3 Continued Statements Reasons 1. N P; NO || MP 1. Given 2. NOM PMO 2. Alt. Int. s Thm. 3. MO MO 3. Reflex. Prop. of 4. ∆MNO ∆OPM 4. AAS 5. NMO POM 5. CPCTC 6. MN || OP 6. Alt. Int. s Thm. Holt McDougal Geometry