Download Major arc

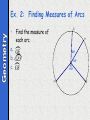
Geometry
Geometry
9.3 Arcs and Central Angles
Geometry
Objectives
• At the completion of the lesson, you
will be able to…
• Define and identify arcs and central
angles in circles
• Calculate the measures of arcs and
central angles in circles
Geometry
Using Arcs of Circles
Central Angle – an angle
whose vertex is at the
center of a circle
Major Arc – formed by two
points on a circle and its
measure is greater than
180; named with 3
endpoints
Minor Arc – formed by two
points on a circle whose
measure is less than 180;
named with 2 endpoints
central angle
A
major
arc
minor
arc
P
B
C
Semicircle – an arc formed
by two points on a circle
whose measure is equal to
180
Example: Naming Arcs
Geometry
G
• Name:
60°
– minor arcs:
60°
•B
E
– major arcs:
H
F
– semicircles:
– An acute central
angle:
– Two congruent arcs:
E
180°
Measuring arcs
Geometry
G
Measure of an arc:
equal to the
measure of an arc’s •B
E
central angle
Minor arc:
Major arc – think
about it: how would I
find
60°
60°
H
F
E
180°
Geometry
A postulate
Arc Addition Postulate
• The measure of the arc
formed by two adjacent
arcs is the sum of the
measures of these two
arcs.
C
A

 
B
m ABC = m AB + m BC
Geometry
Ex. 1: Finding Measures of Arcs
•
Find the measure
of each arc of
R.
a. MN
b. MPN
c. PMN


N
80°
R
M
P
Geometry
Ex. 2: Finding Measures of Arcs
•
Find the measure of
each arc.
G


H
a.
GE
b. G EF
c. GF
40°
80°
R
110°
F
E
Geometry
Congruent arcs
• Arcs, in the same
circle or in congruent
circles, that have
equal measures
•
 
 
AB and DC are in
the same circle and
m AB = m DC= 45°.
So, AB  DC
A
D
B
45°
45°
C
Geometry
Homework
• Page 341 Classroom exercises 1-13
• Page 341 Written Exercises 1-8
• Quiz tomorrow on 9.1-9.3