Download Powerpoint slides

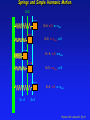
Lecture 21:
Ideal Spring and Simple Harmonic Motion

New Material: Textbook Chapters 10.1, 10.2 and 10.3
Physics 101: Lecture 21, Pg 1
Ideal Springs

Hooke’s Law: The force exerted by a spring is
proportional to the distance the spring is stretched or
compressed from its relaxed position (for small x).
FX = -k x
Where x is the displacement from
the relaxed position and k is the
constant of proportionality.
(often called “spring constant”)
SI unit of k: [N/m]
relaxed position
FX = 0
x
x=0
Physics 101: Lecture 21, Pg 2
Ideal Springs

Hooke’s Law: The force exerted by a spring is
proportional to the distance the spring is stretched or
compressed from its relaxed position.
FX = -k x
Where x is the displacement from
the relaxed position and k is the
constant of proportionality.
(often called “spring constant”)
relaxed position
FX = -kx > 0
x
x0
x=0
Physics 101: Lecture 21, Pg 3
Ideal Springs

Hooke’s Law: The force exerted by a spring is
proportional to the distance the spring is stretched or
compressed from its relaxed position.
FX = -k x
Where x is the displacement from
the relaxed position and k is the
constant of proportionality.
(often called “spring constant”)
relaxed position
FX = - kx < 0
x
x>0
x=0
Physics 101: Lecture 21, Pg 4
Simple Harmonic Motion
Consider the friction-free motion of an object attached
to an ideal spring, i.e. a spring that behaves according to
Hooke’s law.
How does displacement, velocity and acceleration
of the object vary with time ?
Analogy:
Simple harmonic motion along x
<-> x component of uniform circular motion
Physics 101: Lecture 21, Pg 5
What does moving along a circular path have to do with
moving back & forth in a straight line (oscillation about
equilibrium) ??
x = R cos  = R cos (wt)
since  = w t
x
x
1
1
2
R
3
R
8

2
8
7
3
y
7
4
6
5
0
-R

2

4

3
2
6
5
Physics 101: Lecture 21, Pg 6
Velocity and Acceleration

Using again the reference circle one finds for the
velocity
v = - vT sin  = - A w sin (w t)
and for the acceleration
a = - ac cos  = - A w2 cos (w t)
with w in [rad/s]
Physics 101: Lecture 21, Pg 7
Concept Question
A mass on a spring oscillates back & forth with simple harmonic motion
of amplitude A. A plot of displacement (x) versus time (t) is shown
below. At what points during its oscillation is the speed of the block
biggest?
1. When x = +A or -A (i.e. maximum displacement)
2. When x = 0 (i.e. zero displacement)
CORRECT
3. The speed of the mass is constant
x
+A
t
-A
Physics 101: Lecture 21, Pg 8
Concept Question
A mass on a spring oscillates back & forth with simple harmonic motion
of amplitude A. A plot of displacement (x) versus time (t) is shown
below. At what points during its oscillation is the magnitude of the
acceleration of the block biggest?
1. When x = +A or -A (i.e. maximum displacement)
CORRECT
2. When x = 0 (i.e. zero displacement)
3. The acceleration of the mass is constant
x
+A
t
-A
Physics 101: Lecture 21, Pg 9
Springs and Simple Harmonic Motion
X=0
X=A; v=0; a=-amax
X=0; v=-vmax; a=0
X=-A; v=0; a=amax
X=0; v=vmax; a=0
X=A; v=0; a=-amax
X=-A
X=A
Physics 101: Lecture 21, Pg 10
Simple Harmonic Motion:
At t=0 s, x=A
or
x(t) = [A]cos(wt)
v(t) = -[Aw]sin(wt)
a(t) = -[Aw2]cos(wt)
At t=0 s, x=0 m
x(t) = [A]sin(wt)
OR
v(t) = [Aw]cos(wt)
a(t) = -[Aw2]sin(wt)
xmax = A
Period = T (seconds per cycle)
vmax = Aw
Frequency = f = 1/T (cycles per second)
amax = Aw2
Angular frequency = w = 2f = 2/T
For spring: w2 = k/m
Physics 101: Lecture 21, Pg 11
Elastic Potential Energy

Work done by the (average) restoring force of the spring
is
W = |Fave| s cos  = ½ k ( x0+xf) (x0-xf) =
= ½ k (x02 – xf2) = Epot,elastic,0- Epot,elastic,f
The elastic potential energy
Epot,elastic = ½ k x2
has to be considered in addition to kinetic and gravitational
potential energy when calculating the total mechanical
energy of an object.
Physics 101: Lecture 21, Pg 12