Download Document

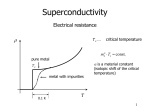
4. The critical magnetic field
The critical current density and
the critical magnetic field
The supercurrent density has a limit: JC
When the superconductor is applied with a magnetic field, a
supercurrent is generated so as to maintain the perfect
diamagnetism. If the current density needed to screen the
field exceeds JC, the superconductor will lose its
superconductivity. This limit of the field strength is called the
critical magnetic field HC.
Note the difference between the flux density, B and field
strength, H
Free energy
The magnetisation depends on the applied field and temperature but
not the history.
The transition is a reversible process
the Gibbs free energy g s (T , H a )
is a function of temperature and field.
Why Gibbs free energy?
Because the system is in contact with a thermal reservoir,
(T=constant) a pressure reservoir (P=constant), and a
“magnetic-field reservoir”(H=constant)
In this case, the system will minimize the Gibbs free energy
Below TC
The free energy of the superconducting state < The free energy
of the normal state
g s (T , 0 ) < g n (T , 0 )
The free energy increases when applied a magnetic field:
∆g ( H a ) = − µ0
Ha
∫ MdH
a
0
Area of the M-H curve
Here we neglect the effect of demagnetizing factor
Free energy
g s (T , H a ) = g s (T , 0 ) − µ0
g s (T , H a )
Ha
∫ MdH
a
g n (T , 0 )
g n (T , H a )
0
= g s ( T , 0 ) + µ0
Ha
∫ HdH
0
a
g s (T , 0 )
H a2
= g s ( T , 0 ) + µ0
2
HC
H
The normal state is non-magnetic and the applied field does
not change the free energy much.
When g s (T , H ) > g n (T , H ) the superconductivity is destryed .
H C2
µ0
= g n (T , 0 ) − g s (T , 0 )
2
The temperature dependence
Phase diagram
H
Normal state
H0
HC
SC
TC
Experimental result:
T
⎡ ⎛ T ⎞2 ⎤
H C = H 0 ⎢1 − ⎜ ⎟ ⎥ = H 0 (1 − t 2 )
⎢⎣ ⎝ TC ⎠ ⎥⎦
The cryotron
Gate(Ta)
Current I
When iC is applied, the field may
destroy the superconductivity of the
gate and reduce the current I
iC
Control(Nb)
An electronic switch
The M-H curve
Deep inside the superconductor
M
B
HC
HC
H
area: the free energy contributed by M
For a perfect specimen, the curves are reversible
H
The hysteresis: non-ideal specimens
Residual magnetization: trapped flux
• Ill defined HC
• Hysteresis
• Trapped flux
Measurement of B
C: pick-up coil
S: solenoid to apply the
field
When the switch is closed,
the ballistic galvanometer
is deflected. The deflection
of G is proportional to B.
LR circuit
Ta at 3.7K
Measurement of magnetization
VSM
The specimen is moved to and
fro between pick-up coils A and
B.
The galvanometer swings with
an amount proportional to the
magnetization M.
Integrating method
E = E A − EB
d
d
∝ µ0 ( H + M ) − µ0 H
dt
dt
dM
E∝
dt
Integrator:
Vout ∝ ∫ Vin dt ∝ M
cf: AC susceptometer
Homework
1. Use the definition of Gibbs free energy G = U − TS + PV − µ0 H a M
to show the Gibbs free energy change due to a magnetic field Ha
is given by.
H
∆g ( H a ) = − µ0 ∫ MdH a
a
0
5. Thermodynamics
Entropy
From
We have
H C2
µ0
= g n (T , 0 ) − g s (T , 0 )
2
µ0
H
(
2
2
C
− H a2 ) = g n (T , 0 ) − g s (T , H a )
G = U − TS + PV − µ0 H a M
dG = dU − d (TS ) + d ( PV ) − µ0 d ( H a M )
= − SdT + VdP − µ0 MdH a
entropy
thus
since
⎛ ∂g ⎞
s = −⎜
⎟
∂
T
⎝
⎠ p,Ha
HC is temperature dependent
dH C
sn − s s = µ 0 H C
dT
dH C
<0
dT
sn > s s
The superconducting state is more
“order” than the normal state
H
Normal state
H0
HC
SC
TC
T
At TC , HC=0
sn = s s
According to the third
law of thermodynamics,
sn = s s
sn = s s
at T=0
Since H0 is finite, this
requires that
dH C
=0
dT
at T=0
Entropy vs temperature
2nd order phase transitions
At TC
sn = s s
⎛ ∂g ⎞ ⎛ ∂g ⎞
⎜
⎟ =⎜
⎟
T
T
∂
∂
⎝
⎠n ⎝
⎠s
∂g
Both g and its derivative
are continuous
∂T
A 2nd order transition
Features: no latent heat
L = vT ( ss − sn )
a jump in specific heat
∂s
C = vT
∂T
Specific heat
2
⎡
∂ ( s s − sn )
d 2 H C ⎛ dH C ⎞ ⎤
Cs − Cn = vT
= vT µ0 ⎢ H C
+⎜
⎟ ⎥
∂T
dT
dT
⎝
⎠ ⎥⎦
⎢⎣
At TC
, HC=0
( Cs − Cn )T
C
Jump at TC
2
⎛ dH C ⎞
= vTC µ0 ⎜
⎟
⎝ dT ⎠TC
Rutger’s formula
Latent heat at non-zero field
dH C
L = vT ( ss − sn ) = −vT µ0 H C
dT
H
H0
Normal state
sn > s s
1st order transition
SC
2nd order transition
TC
T
Adiabatic magnetization
Adiabatic process, s=constant
dQ = TdS = 0
Adiabatically destructing
the superconductivity by
applying a large field can
lower the temperature
Adiabatic demagnetization
Is used for ordinary
magnetic materials in which
the entropy decreases with
application of field.
Specific heat
The specific heat of a metal is contributed from the lattice and
conduction electrons
C = Clatt + Cel
The properties of the lattice do not change at the transition
Cs − Cn = ( Cel ) s − ( Cel )n
For a normal metal
Cn = Clatt + ( Cel )n
θ: Debye temperature
3
⎛T ⎞
= A⎜ ⎟ + γ T
⎝θ ⎠
γ: Sommerfeld constant
At T ~TC
C s > Cn
because sn > ss
dS s dS n
>
dT
dT
At low temperature
C s < Cn
Cn A 2
= 3 T +γ
T θ
C/T
At T<TC , one can measure C for
normal state (Ha>HC)
The electronic part for superconducting
state can be determined
− b / kT
C
=
ae
( el )s
Slope=A/θ
γ
TC
T2
The form of the thermal activation : hint of a energy gap b/e
As T approaches TC, b rapidly decreases to zero
Irreversible processes
Thermal conduction
The thermal conduction in a metal is mostly contributed by
the conduction electrons
Superelectrons have negligible interaction with the lattice
The thermal conductivity in superconducting state is much
smaller than that in normal state.
Thermoelectric effects
Due to zero resistance of the superconductors, the thermal
e.m.f. should be zero. Therefore, Peltier and Thomson
coefficients are zero.
In fact, thermoelectric effects may appear in type-II
superconductors
Seebeck(thermoelectric) effect
e.m.f. due to temperature
gradient under conditions of
zero electric current
A
T1
B
Peltier effect
Heat flow following an
electric current across an
isothermal junction
A
V
B
current
Heat flow
Thomson effect
Electric current traverses a
temperature gradient
T2
T1
T2
current
Homework
1. Apply Sommerfeld’s theory to show that the electronic
specific heat of the metals is proportional to the temperature, i. e.
Cel = γ T
in which the constant γ is proportional to the density of states at
Fermi surface.
2. Do the same calculation by assuming an energy gap ∆
forming at the Fermi surface and show that
Cel = ae − e∆ / kT
at low temperature, kT<<∆