Download Intro to light

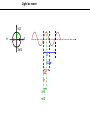
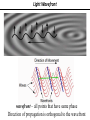
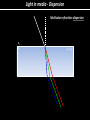
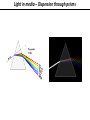
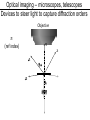
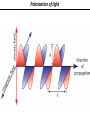
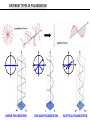
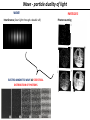
Introduction to Light
Stolen from Florin Albeanu
2016/07/19
Light as an oscillating electro-magnetic field
ELECTRO-MAGNETIC RADIATION:
Light as an oscillating electro-magnetic field
Wavelength (λ)
Amplitude (A)
Intensity
I α A2
Frequency
ν=λ/c
z
direction of propagation
Phase (φ)
π/2
π
t3210
z0
z
0
3π/2
Light oscillating electric field:
E (x,t) = A sin(kx – ωt + ε)
E (x,t) = A e i(kx – ωt + ε)
k = 2π/λ;
ω = 2π*ν; ε initial phase
Light as wave
π/2
π
0
3π/2
λ
0-2π
λ/2
π
λ/4
π/2
Superposition of waves
• Superposition: point by point addition of amplitude of light waves
• Superposition of light waves generates interference patterns
• Relative phases determine whether the interference is constructive vs. destructive
π/2
π
0
2π
3π/2
0-2π
π
π/2
constructive interference
destructive interference
intermediate interference
Light Wavefront
wavefront – all points that have same phase
Direction of propagation is orthogonal to the wavefront
Light Wavefront
spherical wavefronts turn into planar wavefronts with
increasing distance from the source
Huygens Principle
The wavefront of a propagating wave of light at
any instant conforms to the envelope of
spherical wavelets emanating from every point
on the wavefront at the prior instant
Reflection and Huygens Principle
Light in vacuum
• Light (EMR) propagates in vacuum at a speed: c
• Speed = distance/time = λ / T = λ * ν = 300*106 m/s
nanometers femtoseconds
• The speed of EMR is constant in vacuum
~1015Hz
c
• … but it decreases when light travels through media
Light in media
Light in media
Principle of least time – Pierre Fermat
Reflection
θ1
θ1 '
n1
n2
θ2
n2 > n1
Law of refraction (Snell’a law):
n1 sinθ1 = n2 sinθ2
n1 = c/v1, n2=c/v2
Refraction
Law of reflection:
θ1 = θ1 ’
Refraction and Huygens Principle
Wavefronts have to be continuous!
Refraction… car in mud analogy
Light in media
Light slows down in media.
How are the frequency and wavelength impacted?
Light slows down – less distance traveled per cycle
Frequency stays constant across media
Wavelength changes
Light in media - Dispersion
Multicolor refraction: dispersion
n1
n2
1 < nred < ngreen < nblue
vblue < vgreen < vred < c
n2 > n1
Light in media – Dispersion through prisms
Diffraction and resolution in microscopy
Superposition of two spherical wavefronts
Constructive
interference
Destructive
interference
Constructive
interference
Optical path difference
Light waves emitting from the two slits
interferes – constructively or destructively
depending on the difference in traveled distance
Assumption holds for L >> d
d
~θ
θ
θ
d*sin θ
L >> d
CONSTRUCTIVE INTERFERENCE: d*sinθ = mλ
DESTRUCTIVE INTERFERENCE:
m = 1, 2, 3 …
d*sin θ = (m + 0.5) λ
The smaller the distance d between the slits, the bigger the diffraction angle θ
mλ
d=
sinθ
Information about the fine spatial detail (small slits) in the sample, is
contained in higher diffraction orders – large angles
Information about the coarse spatial detail (big slits) in the
sample is contained in lower diffraction orders – smaller angles
Optical imaging – microscopes, telescopes
Devices to steer light to capture diffraction orders
Objective
𝑛
(ref index)
Numerical aperture
Relationship between resolution and NA
D
pupil plane
θ
f
n
focal plane
D = 2 f NA = 2 f n sin θ
d = λ / sin θ
Rmin(x,y) ~ λ / NA
Polarization of light
DIFFERENT TYPES OF POLARIZATION
LINEAR POLARIZATION
CIRCULAR POLARIZATION
ELLIPTICAL POLARIZATION
Birefringence is the optical property of a material having a
refractive index that depends on the polarization and
propagation direction of light.
λ/2 and λ/4 waveplates
Is light really a wave?
Intensity (J/m2) ~ amplitude of the light electric field
Energy (J) ~ frequency of the light electro-magnetic field
Light oscillating electric field:
E (x,t) = A sin(kx – ωt + ε)
k = 2π/λ;
ω = 2π*ν; ε initial phase
PHOTOELECTRIC EFFECT
e
Frequency threshold : below this threshold, no
electrons are emitted, even if intensity is increased
e
e
METAL
Classical wave theory of light:
increasing either the frequency or the
intensity of light would increase
electron emission rate
BUT
Light propagates as discrete packets of energy called
PHOTONS:
Energy = hν
h: Plank’s constant
Wave - particle duality of light
WAVE!
Interference (laser light through a double slit)
ELECTRO-MAGNETIC WAVE AS STATISTICAL
DISTRIBUTION OF PHOTONS
PARTICLES!
Photon counting
Wave - particle duality of light
PARTICLES
WAVE
Diffraction pattern of a laser
beam through a pinhole
Sequence of images acquired with a position sensitive
photo-multiplier tube illuminated by an image of a bar
chart (exposure times at 8, 125, 1000, 10000 ms)
Laser light through a double slit
"It seems as though we must use sometimes the one
theory and sometimes the other, while at times we may
use either. (…) We have two contradictory pictures of
reality; separately neither of them fully explains the
phenomena of light, but together they do"