Download Summary presentation 12.2 alternating currents File

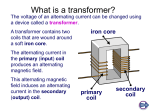
Electromagnetism
Topic 12.2 Alternating Current
Rotating Coils
Most of our electricity comes from huge
generators in power stations.
 There are smaller generators in cars and
on some bicycles.
 These generators, or dynamos, all use
electromagnetic induction.
 When turned, they induce an EMF
(voltage) which can make a current flow.







The next diagram shows a simple AC generator.
It is providing the current for a small bulb.
The coil is made of insulated copper wire and is
rotated by turning the shaft.
The slip rings are fixed to the coil and rotate
with it.
The brushes are two contacts which rub against
the slip rings and keep the coil connected to the
outside part of the circuit.
They are usually made of carbon.
AC Generator





When the coil is rotated, it cuts magnetic field
lines, so an EMF is generated.
This makes a current flow.
As the coil rotates, each side travels upwards,
downwards, upwards, downwards... and so on,
through the magnetic field.
So the current flows backwards, forwards... and
so on.
In other words, it is AC.
The graph shows how the current varies
through one cycle (rotation).
 It is a maximum when the coil is horizontal
and cutting field lines at the fastest rate.
 It is zero when the coil is vertical and
cutting no field lines.

AC Generator Output
The Sinusoidal Shape

As the emf can be calculated from

ε = - N Δ (Φ/ Δt)
and Φ = AB cos θ
It can be clearly seen that the shape of the curve
must be sinusoidal.


The following all increase the maximum
EMF (and the current):
 increasing the number of turns on the coil
 increasing the area of the coil
 using a stronger magnet
 rotating the coil faster.
 (rotating the coil faster increases the
frequency too!)

Alternating Current
The graph shows the values of V and I
plotted against time
 Can you see that the graphs for both V
and I are sine curves?
 They both vary sinusoidally with time.
 Can you see that the p.d. and the current
rise and fall together?
 We say that V and I are in phase.


The time period T of an alternating p.d. or
current is the time for one complete cycle. This
is shown on the graph

The frequency f of an alternating pd or current is
the number of cycles in one second.

The peak values V0 and I0 of the alternating p.d.
and current are also shown on the graph
Root Mean Square Values
How do we measure the size of an
alternating p.d. (or current) when its value
changes from one instant to the next?
 We could use the peak value, but this
occurs only for a moment.
 What about the average value?
 This is zero over a complete cycle and so
is not very helpful!

In fact, we use the root-mean-square
(r.m.s.) value.
 This is also called the effective value.
 The r.m.s. value is chosen, because it is
the value which is equivalent to a steady
direct current.

You can investigate this using the
apparatus in the diagram
 Place two identical lamps side by side.
 Connect one lamp to a battery; the other
to an a.c. supply.
 The p.d. across each lamp must be
displayed on the screen of a double-beam
oscilloscope.

Adjust the a.c. supply, so that both lamps
are equally bright
 The graph shows a typical trace from the
oscilloscope We can use it to compare the
voltage across each lamp.





Since both lamps are equally bright, the d.c. and
a.c. supplies are transferring energy to the bulbs
at the same rate.
Therefore, the d.c. voltage is equivalent to the
a.c. voltage.
The d.c. voltage equals the r.m.s. value of the
a.c. voltage.
Notice that the r.m.s. value is about 70% (1/√2)
of the peak value.

In fact:
Why √2
Why The power dissipated in a lamp
varies as the p.d. across it, and the current
passing through it, alternate.
 Remember power,P = current,(I) x p.d., (V)


If we multiply the values of I and V at any
instant, we get the power at that moment
in time, as the graph shows
The power varies between I0V0 and zero.
 Therefore average power = I0V0 / 2


Or P = (I0 / √ 2) x (V0 / √ 2)

Or P = Irms x Vrms
Root Mean Square Voltage
Root Mean Square Current
Calculations
Use the rms values in the normal
equations}
 Vrms = Irms R
 P = Irms Vrms
 P = Irms2 R
 P = Vrms2 / R

Transformers
A transformer changes the value of an
alternating voltage.
 It consists of two coils, wound around a
soft-iron core, as shown


In this transformer, when an input p.d. of 2
V is applied to the primary coil, the output
pd. of the secondary coil is 8V
How does the transformer
work?




An alternating current flows in the primary coil.
This produces an alternating magnetic field in
the soft iron core.
This means that the flux linkage of the
secondary coil is constantly changing and so an
alternating potential difference is induced across
it.
A transformer cannot work on d.c.
An Ideal Transformer
This is 100% efficient
 Therefore the power in the primary is
equal to the power in the secondary
 Pp = Ps
 i.e. Ip Vp = Is Vs

Step-up Step-down
A step-up transformer increases the a.c.
voltage, because the secondary coil has
more turns than the primary coil.
 In a step-down transformer, the voltage is
reduced and the secondary coil has fewer
turns than the primary coil.

The Equation
Note:
 • In the transformer equations, the
voltages and currents that you use must
all be peak values or all r.m.s. values.
 Do not mix the two.
 Strictly, the equations apply only to an
ideal transformer, which is 100 % efficient.
