* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Exam I Review Math 1530: Elements of Statistics Type of variables
Survey
Document related concepts
Transcript
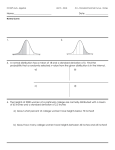
Exam I Review Math 1530: Elements of Statistics Type of variables: 1. The brand of soda is 2. The number of cars sold in a week is 3. The time until the tenth car is sold is 4. The number of coins in your pocket is 5. Outcomes of the variable depend on values of the variable. Which of the following thirteen statements are true, and which are false? 6. The standard deviation measures how far the data tend to be from 0. 7. When data contains extreme observations (outliers), IQR can be a good measure of spread. 8. A z-score tells the direction and number of means a data value is from the standard deviation. 9. The median lies to the right of the mean for a right-skewed distribution. 10. The regression line has the property that the sum of the squared errors (or sum of squared residuals) is as large as possible. 11. The first quartile divides a data set into a lower 75% and upper 25%. 12. About 99.7% of a population with a bell-shaped distribution lies within two standard deviations of the mean. 13. Approximately 25% of a population are above the third quartile. 14. Influential observations tend to lie far from most of the other data points, and they can have a large influence on the regression line. 15. The less spread out data are from their mean, the larger the standard deviation is. 16. Data with an r value of -0.98 are strongly correlated. 17. Two data sets with the same standard deviation should have the same mean. 18. If the correlation between two quantitative variables is 0.10, the variables have a strong linear relationship. Use the following information to answer the next seven questions. 19. What is the shpe of the Squad 1’s distribution? 20. Which squad had the lowest median number of zombies killed? 21. Based on the IQR, which squad had the largest spread? 22. What is the minimum value for Zombie Attack Squad 1? 23. What is the value of IQR for the Squad 3? 24. About what percent of Squad 2 killed more than 18 zombies? 25. The dot plot below represents one of the data sets displayed in the Zombie Attack boxplots above. Which squad do you think it represents? The remaining questions on this page refer to the histogram below showing the hours worked per week for a sample of 39 statistics students for fall 2011. 26. How many students worked at least 10 hours but less than 20 hours? 27. What is the shape of this distribution? 28. How many students worked at least 15 hours per week? 29. What percent of the students worked less than 10 hours? The following are Kelley Blue Book values for a Ford F-150 based on truck age in years. Age (years) Value ($) 1 2 3 4 5 16,905 15,450 11,700 11,380 9,935 We want to predict the value of a Ford F-150 based on its age. The following questions refer to the above data. 30. What is the equation of the regression line? 31. What is the value of the correlation coefficient r, correct to two decimal places? 32. According to this regression model, what percent of the variation in the price of a used Ford F-150 truck is explained by its age? 33. Is the regression line a good model for this data set? Why or why not? 34. Use the regression line model to predict the dollar of a 10 year old Ford F-150. 35. Would this regression line be useful for predicting the value of a 10 year-old F-150? Why? 36. A potential lurking variable might be (i) the condition of the F-150 (a) i (ii) the number of miles driven per year (b) ii (c) iii (iii) the price of eggs (d) i and ii (e) i, ii, and iii Christmas tree heights have a bell-shaped distribution with mean 65 inches and standard deviation 9 inches. A farmer samples 1000 trees. Use this to answer the next three questions. 37. One tree had a z-score of 3.25. Which is correct? (a) This tree height is 3.25 standard deviation below the mean (b) This tree height is 3.25 inches above the mean (c) This tree height can be considered as an outlier from the other tree heights (d) This tree height is about average 38. Approximately what percentage of the tree heights fall between 56 and 74 inches? 39. Approximately how many trees have heights between 47 and 83 inches tall? Consider the data 6, 7, 10, 13. You must show your work. 40. What is the mean? Answer: 41. What is the sample standard deviation? x x−x (x − x)2 6 7 10 13 Total: Answer: The demand for snow cones each day for nine consecutive days was 21 20 23 25 21 33 25 26 21 Use this information to answer the following four questions. You must show your work. 42. What is the median? Answer: 43. What is the range? Answer: 44. What is the interquartile range? Answer: 45. Use the lower limit and upper limit rule to identify outliers. Answer: