Download Chapter 13 Oscillations about Equilibrium

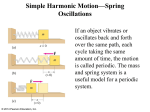
Chapter 13
Oscillations about
Equilibrium
Copyright © 2010 Pearson Education, Inc.
Units of Chapter 13
• Periodic Motion
• Simple Harmonic Motion
• Connections between Uniform Circular
Motion and Simple Harmonic Motion
• The Period of a Mass on a Spring
• Energy Conservation in Oscillatory
Motion
Copyright © 2010 Pearson Education, Inc.
Units of Chapter 13
• The Pendulum
• Damped Oscillations
• Driven Oscillations and Resonance
Copyright © 2010 Pearson Education, Inc.
13-1 Periodic Motion
Period: time required for one cycle of periodic
motion
Frequency: number of oscillations per unit
time
This unit is
called the Hertz:
Copyright © 2010 Pearson Education, Inc.
13-2 Simple Harmonic Motion
A spring exerts a restoring force that is
proportional to the displacement from
equilibrium:
Copyright © 2010 Pearson Education, Inc.
13-2 Simple Harmonic Motion
A mass on a spring has a displacement as a
function of time that is a sine or cosine curve:
Here, A is called
the amplitude of
the motion.
Copyright © 2010 Pearson Education, Inc.
13-2 Simple Harmonic Motion
If we call the period of the motion T – this is the
time to complete one full cycle – we can write
the position as a function of time:
It is then straightforward to show that the
position at time t + T is the same as the
position at time t, as we would expect.
Copyright © 2010 Pearson Education, Inc.
13-3 Connections between Uniform Circular
Motion and Simple Harmonic Motion
An object in simple
harmonic motion has the
same motion as one
component of an object
in uniform circular
motion:
Copyright © 2010 Pearson Education, Inc.
Here, the object in circular motion has an
angular speed of
where T is the period of motion of the
object in simple harmonic motion.
Copyright © 2010 Pearson Education, Inc.
13-3 Connections between Uniform Circular
Motion and Simple Harmonic Motion
The position as a function of time:
The angular frequency:
Copyright © 2010 Pearson Education, Inc.
Question 13.1a Harmonic Motion I
A mass on a spring in SHM has
a) 0
amplitude A and period T. What
b) A/2
is the total distance traveled by
c) A
the mass after a time interval T?
d) 2A
e) 4A
Question 13.1a Harmonic Motion I
A mass on a spring in SHM has
a) 0
amplitude A and period T. What
b) A/2
is the total distance traveled by
c) A
the mass after a time interval T?
d) 2A
e) 4A
In the time interval T (the period), the mass goes
through one complete oscillation back to the starting
point. The distance it covers is A + A + A + A (4A).
Question 13.1b Harmonic Motion II
A mass on a spring in SHM has
amplitude A and period T. What is
the net displacement of the mass
after a time interval T?
a) 0
b) A/2
c) A
d) 2A
e) 4A
Question 13.1b Harmonic Motion II
A mass on a spring in SHM has
amplitude A and period T. What is
the net displacement of the mass
after a time interval T?
a) 0
b) A/2
c) A
d) 2A
e) 4A
The displacement is Δx = x2 – x1. Because the
initial and final positions of the mass are the
same (it ends up back at its original position),
then the displacement is zero.
Follow-up: What is the net displacement after a half of a period?
Question 13.1c Harmonic Motion III
A mass on a spring in SHM has
amplitude A and period T. How
long does it take for the mass to
travel a total distance of 6A ?
a) ½T
b) ¾T
c) 1¼T
d) 1½T
e) 2T
Question 13.1c Harmonic Motion III
A mass on a spring in SHM has
amplitude A and period T. How
long does it take for the mass to
travel a total distance of 6A ?
a) ½T
b) ¾T
c) 1¼T
d) 1½T
e) 2T
1 2
We have already seen that it takes one period T to travel a total
distance of 4A. An additional 2A requires half a period, so the total
time needed for a total distance of 6A is 1 T.
Follow-up: What is the net displacement at this particular time?
13-3 Connections between Uniform Circular
Motion and Simple Harmonic Motion
The velocity as a function of time:
Found by taking x components of
the circular motion quantities.
Copyright © 2010 Pearson Education, Inc.
13-3 Connections between Uniform Circular
Motion and Simple Harmonic Motion
The acceleration:
Found by taking x components of
the circular motion quantities.
Copyright © 2010 Pearson Education, Inc.
Question 13.2 Speed and Acceleration
A mass on a spring in SHM has
a) x = A
amplitude A and period T. At
b) x > 0 but x < A
what point in the motion is v = 0
c) x = 0
and a = 0 simultaneously?
d) x < 0
e) none of the above
Question 13.2 Speed and Acceleration
A mass on a spring in SHM has
a) x = A
amplitude A and period T. At
b) x > 0 but x < A
what point in the motion is v = 0
c) x = 0
and a = 0 simultaneously?
d) x < 0
e) none of the above
If both v and a were zero at
the same time, the mass
would be at rest and stay at
rest! Thus, there is NO
point at which both v and a
are both zero at the same
time.
Follow-up: Where is acceleration a maximum?
13-4 The Period of a Mass on a Spring
Since the force on a mass on a spring is
proportional to the displacement, and also to
the acceleration, we find that
.
Substituting the time dependencies of a and x
gives
Copyright © 2010 Pearson Education, Inc.
13-4 The Period of a Mass on a Spring
Therefore, the period is
Copyright © 2010 Pearson Education, Inc.
Question 13.6a Period of a Spring I
A glider with a spring attached to
each end oscillates with a certain
period. If the mass of the glider is
doubled, what will happen to the
period?
a) period will increase
b) period will not change
c) period will decrease
Question 13.6a Period of a Spring I
A glider with a spring attached to
each end oscillates with a certain
period. If the mass of the glider is
doubled, what will happen to the
period?
a) period will increase
b) period will not change
c) period will decrease
The period is proportional to the
square root of the mass. So an
increase in mass will lead to an
increase in the period of motion.
m
T = 2π
k
Follow-up: What happens if the amplitude is doubled?
(a)
(b)
13-5 Energy Conservation in Oscillatory
Motion
In an ideal system with no nonconservative
forces, the total mechanical energy is
conserved. For a mass on a spring:
Since we know the position and velocity as
functions of time, we can find the maximum
kinetic and potential energies:
Copyright © 2010 Pearson Education, Inc.
13-5 Energy Conservation in Oscillatory
Motion
As a function of time,
So the total energy is constant; as the
kinetic energy increases, the potential
energy decreases, and vice versa.
Copyright © 2010 Pearson Education, Inc.
13-5 Energy Conservation in Oscillatory
Motion
This diagram shows how the energy
transforms from potential to kinetic and
back, while the total energy remains the
same.
Copyright © 2010 Pearson Education, Inc.
Question 13.5a Energy in SHM I
A mass oscillates in simple
harmonic motion with amplitude
A. If the mass is doubled, but the
amplitude is not changed, what
will happen to the total energy of
the system?
a) total energy will increase
b) total energy will not change
c) total energy will decrease
Question 13.5a Energy in SHM I
A mass oscillates in simple
harmonic motion with amplitude
A. If the mass is doubled, but the
amplitude is not changed, what
will happen to the total energy of
the system?
a) total energy will increase
b) total energy will not change
c) total energy will decrease
1 2
The total energy is equal to the initial value of the
elastic potential energy, which is PEs = kA2. This
does not depend on mass, so a change in mass will
not affect the energy of the system.
Follow-up: What happens if you double the amplitude?
13-6 The Pendulum
A simple pendulum consists of a mass m (of
negligible size) suspended by a string or rod of
length L (and negligible mass).
The angle it makes with the vertical varies with
time as a sine or cosine.
Copyright © 2010 Pearson Education, Inc.
13-6 The Pendulum
Looking at the forces
on the pendulum bob,
we see that the
restoring force is
proportional to sin θ,
whereas the restoring
force for a spring is
proportional to the
displacement (which
is θ in this case).
Copyright © 2010 Pearson Education, Inc.
13-6 The Pendulum
However, for small angles, sin θ and θ are
approximately equal.
Copyright © 2010 Pearson Education, Inc.
13-6 The Pendulum
Substituting θ for sin θ allows us to treat the
pendulum in a mathematically identical way to
the mass on a spring. Therefore, we find that
the period of a pendulum depends only on the
length of the string:
Copyright © 2010 Pearson Education, Inc.
13-7 Damped Oscillations
In most physical situations, there is a
nonconservative force of some sort, which will
tend to decrease the amplitude of the
oscillation, and which is typically proportional
to the speed:
This causes the amplitude to decrease
exponentially with time:
Copyright © 2010 Pearson Education, Inc.
13-7 Damped Oscillations
This exponential decrease is shown in the
figure:
Copyright © 2010 Pearson Education, Inc.
13-7 Damped Oscillations
The previous image shows a system that is
underdamped – it goes through multiple
oscillations before coming to rest. A critically
damped system is one that relaxes back to the
equilibrium position without oscillating and in
minimum time; an overdamped system will
also not oscillate but is damped so heavily
that it takes longer to reach equilibrium.
Copyright © 2010 Pearson Education, Inc.
13-8 Driven Oscillations and Resonance
An oscillation can be driven by an oscillating
driving force; the frequency of the driving force
may or may not be the same as the natural
frequency of the system.
Copyright © 2010 Pearson Education, Inc.
13-8 Driven Oscillations and Resonance
If the driving frequency
is close to the natural
frequency, the
amplitude can become
quite large, especially
if the damping is small.
This is called
resonance.
Copyright © 2010 Pearson Education, Inc.
Summary of Chapter 13
• Period: time required for a motion to go
through a complete cycle
• Frequency: number of oscillations per unit time
• Angular frequency:
• Simple harmonic motion occurs when the
restoring force is proportional to the
displacement from equilibrium.
Copyright © 2010 Pearson Education, Inc.
Summary of Chapter 13
• The amplitude is the maximum displacement
from equilibrium.
• Position as a function of time:
• Velocity as a function of time:
Copyright © 2010 Pearson Education, Inc.
Summary of Chapter 13
• Acceleration as a function of time:
• Period of a mass on a spring:
• Total energy in simple harmonic motion:
Copyright © 2010 Pearson Education, Inc.
Summary of Chapter 13
• Potential energy as a function of time:
• Kinetic energy as a function of time:
• A simple pendulum with small amplitude
exhibits simple harmonic motion
Copyright © 2010 Pearson Education, Inc.
Summary of Chapter 13
• Period of a simple pendulum:
Copyright © 2010 Pearson Education, Inc.
Summary of Chapter 13
• Oscillations where there is a nonconservative
force are called damped.
• Underdamped: the amplitude decreases
exponentially with time:
• Critically damped: no oscillations; system
relaxes back to equilibrium in minimum time
• Overdamped: also no oscillations, but
slower than critical damping
Copyright © 2010 Pearson Education, Inc.
Summary of Chapter 13
• An oscillating system may be driven by an
external force
• This force may replace energy lost to friction,
or may cause the amplitude to increase greatly
at resonance
• Resonance occurs when the driving frequency
is equal to the natural frequency of the system
Copyright © 2010 Pearson Education, Inc.