Download 9-3 Law of Sines

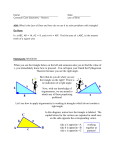
9-3 LAW OF SINES
LAW OF SINES
B
Given an oblique
triangle (no right angle)
we can draw in the altitude
A
from vertex B

c
a
b
Label the altitude k and find
two equations involving k

C
LAW OF SINES

By using the equations for the area of a triangle.
We can obtain the equation for the Law of Sines
by dividing everything by
LAW OF SINES

In triangle ABC the following is true

What are we given?
AAS or ASA Two angles and any side (1 possible
triangle)
 SSA Two sides and an angle opposite from one of
them (ambiguous case: may not be a solution, 1 or 2
solutions)

EXAMPLE #1

A civil engineer wants to determine the distances
from points A and B to an inaccessible point C.
From direct measurement the engineer knows
that AB=25m, <A=110°, and <B=20°. Find AC
and BC.
C
a
b
110°
A
20°
25m
B
EXAMPLE #2

In triangle RST, <S=126°, s=12, and t=7.
Determine whether <T exists. If so, find all
possible measures of <T.
EXAMPLE #3

Solve triangle RST is <S=40°, r=30, and s=20.
Give angle measure to the nearest tenth of a
degree and lengths to the nearest hundredth.
EXAMPLE #4

Solve triangle ABC when <C=112°, c=5, and a=7.
EXAMPLE #4

Solve triangle ABC when <A=30°, a=7, and c=16.