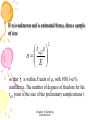Download Sampling Distributions

Chapter 6 Sampling
Distributions(样本分布)
 The Sampling Distribution of
the Sample Mean
 The Sampling Distribution of
the Sample Proportion
Sample Mean
 Let there be a population of units of size N
 Consider all its samples of a fixed size n (n<N)
 For all possible samples of size n, we obtain a
population of sample means. That is, x is a random
variable which may have all these means as its values
 Before we draw the sample, the sample mean x is a
random variable.
 We consider the probability distribution of the random
variable x , i.e., the probability distribution for the
population of sample means
Chapter 6 Sampling
Distributions
Section 6.1 The Sampling Distribution of
the Sample Mean
The sampling distribution of the sample
mean is the probability distribution of the
population of the sample means obtainable
from all possible samples of size n from a
population of size N.
Chapter 6 Sampling
Distributions
The Stock Return Case
• We have a population of the percent returns from six
stocks
– In order, the values of % return are:
10%, 20%, 30%, 40%, 50%, and 60%
• Label each stock A, B, C, …, F in order of
increasing % return
• The mean rate of return is 35% with a standard
deviation of 17.078%
– Any one stock of these stocks is as likely to be picked
as any other of the six
• Uniform distribution with N = 6
• Each stock has a probability of being picked of 1/6
Example 6.1
Chapter 6 Sampling
Distributions
The Stock Return Case ﹟2
Stock
Stock A
Stock B
Stock C
Stock D
Stock E
Stock F
Total
% Return
10
20
30
40
50
60
Frequency
1
1
1
1
1
1
6
Relative
Frequency
1/6
1/6
1/6
1/6
1/6
1/6
1
Chapter 6 Sampling
Distributions
The Stock Return Case ﹟3
• Now, select all possible samples of size n
= 2 from this population of stocks of size
N=6
– That is, select all possible pairs of
stocks
• How to select?
– Sample randomly
– Sample without replacement
– Sample without regard to order
Chapter 6 Sampling
Distributions
The Stock Return Case ﹟4
• Result: There are C 15 possible
samples of size n = 2
• Calculate the sample mean of each and
every sample
• For example, if we choose the two
stocks with returns 10% and 20%, then
the sample mean is 15%
2
6
Chapter 6 Sampling
Distributions
The Stock Return Case ﹟5
Sample
Mean
15
20
25
30
35
40
45
50
55
Relative
Frequency Frequency
1
1/15
1
1/15
2
2/15
2
2/15
3
3/15
2
2/15
2
2/15
1
1/15
1
1/15
Chapter 6 Sampling
Distributions
Observations
• The population of N = 6 stock returns has a
uniform distribution.
• But the histogram of n = 15 sample mean
returns:
1. Seems to be centered over the same mean
return of 35%, and
2. Appears to be bell-shaped and less spread
out than the histogram of individual
returns
Chapter 6 Sampling
Distributions
Example 6.2
Sampling all the stocks
• Consider the population of returns of all
1,815 stocks listed on NYSE for 1987
– See Figure 6.2(a) on next slide
– The mean rate of return  was –3.5%
with a standard deviation  of 26%
• Draw all possible random samples of size n
= 5 and calculate the sample mean return of
each
– Sample with a computer
– See Figure 6.2(b) on next slide
Chapter 6 Sampling
Distributions
Chapter 6 Sampling
Distributions
• Observations
– Both histograms appear to be bell-shaped and
centered over the same mean of –3.5%
– The histogram of the sample mean returns
looks less spread out than that of the individual
returns
• Statistics
– Mean of all sample means: x =  = -3.5%
– Standard deviation of all possible means:

26
x 

 11.63%
n
5
Chapter 6 Sampling
Distributions
General Conclusions
If the population of individual items is
normal, then the population of all sample
means is also normal
Even if the population of individual
items is not normal, there are
circumstances that the population of all
sample means is normal (see Central
Limit Theorem(中心极限定理) later)
Chapter 6 Sampling
Distributions
General Conclusions
• The mean of all possible sample means equals the
population mean
– That is,  =  x
• The standard deviation sx of all sample means is
less than the standard deviation of the population
– That is,  x < 
• Each sample mean averages out the high and
the low measurements, and so are closer to
m than many of the individual population
measurements
Chapter 6 Sampling
Distributions
• The empirical rule holds for the sampling distribution
of the sample mean
– 68.26% of all possible sample means are within
(plus or minus) one standard deviation  x of 
– 95.44% of all possible observed values of x are
within (plus or minus) two  x of 
• In the example., 95.44% of all possible sample
mean returns are in the interval [-3.5 ±
(211.63)] = [-3.5 ± 23.26]
• That is, 95.44% of all possible sample means are
between -26.76% and 19.76%
– 99.73% of all possible observed values of x are
within (plus or minus) three x of 
Chapter 6 Sampling
Distributions
Properties of the Sampling
Distribution of the Sample Mean #1
• If the population being sampled is normal,
then so is the sampling distribution of the
sample mean, x
• The mean  x of the sampling distribution of
is
x
x =
That is, the mean of all possible sample means
is the same as the population mean
Chapter 6 Sampling
Distributions
Properties of the Sampling
Distribution of the Sample Mean #2
• The variance x2 of the sampling distribution
of x is
2

2
x 
n
 That is, the variance of the sampling
distribution of x is
 directly proportional to the variance of
the population, and
 inversely proportional to the sample
size
Chapter 6 Sampling
Distributions
Properties of the Sampling
Distribution of the Sample Mean #3
• The standard deviation  x of the sampling
distribution of x is

x 
n
 That is, the standard deviation of the
sampling distribution of x is
 directly proportional to the standard
deviation of the population, and
 inversely proportional to the square root
of the sample size
Chapter 6 Sampling
Distributions
Notes

is the point estimate of , and the
larger the sample size n, the more
accurate the estimate, because when n
increases,  decreases, x is more
clustered to the population
–In order to reduce x , take bigger
samples!
x
x
Chapter 6 Sampling
Distributions
Car Mileage Case
• Population of all midsize cars of a particular make
and model
– Population is normal with mean  and standard
deviation 
– Draw all possible samples of size n
– Then the sampling distribution of the sample
mean is normal with mean  x =  and standard
deviation  x   n
– In particular, draw samples of size:
•n=5
• n = 49
Example 6.3
Chapter 6 Sampling
Distributions


x 

5 2.2361
x 

49


7
So, all possible sample means for n=49 will be more closely clustered
around  than the case of n =5
Chapter 6 Sampling
Distributions
Reasoning from Sample Distribution
• Recall from Chapter 2 mileage example,
x = 31.5531 mpg for a sample of size n=49
– With s = 0.7992
• Does this give statistical evidence that the
population mean  is greater than 31 mpg?
– That is, does the sample mean give evidence that
 is at least 31 mpg?
• Calculate the probability of observing a sample
mean that is greater than or equal to 31.5531 mpg if
 = 31 mpg
– Want P( x > 31.5531 if  = 31)
Chapter 6 Sampling
Distributions
 Use s as the point estimate for  so that
x 

n

0.7992
 0.1143
49
 Then

31.5531   x 


P x  31.5531 if   31  P z 



x


31.5531  31 

 P z 

0.1143 

 P z  4.84 


 But z = 4.84 is off the standard normal table
 The largest z value in the table is 3.09, which has a
right hand tail area of 0.001
Chapter 6 Sampling
Distributions
Probability that x > 31.5531 when  = 31
Chapter 6 Sampling
Distributions
• z = 4.84 > 3.09, so P(z ≥ 4.84) < 0.001
• That is, if  = 31 mpg, then fewer than 1 in 1,000
of all possible samples have a mean at least as large
as observed
• Have either of the following explanations:
If  is actually 31 mpg, then picking this sample
is an almost unbelievable thing
OR
 is not 31 mpg
• Difficult to believe such a small chance would occur,
so conclude that there is strong evidence that 
does not equal 31 mpg.
–  is in fact larger than 31 mpg
Chapter 6 Sampling
Distributions
Central Limit Theorem
(中心极限定理) #1
If the population is non-normal, what is the shape of
the sampling distribution of the sample means?
In fact the sampling distribution is approximately
normal if the sample is large enough, even if the
population is non-normal
by the “Central Limit Theorem”
Chapter 6 Sampling
Distributions
 No matter what is the probability distribution that
describes the population, if the sample size n is
large enough, then the population of all possible
sample means is approximately normal with
mean  x   and standard deviation  x   n
 Further, the larger the sample size n, the closer
the sampling distribution of the sample means is
to being normal
– In other words, the larger n, the better the
approximation
Chapter 6 Sampling
Distributions
Random Sample (x1, x2, …, xn)
x
X
as n  large
Population Distribution
(, )

(right-skewed)
Sampling
Distribution of
Sample Means
x
 , x  
(nearly normal)
Chapter 6 Sampling
Distributions
n

Example 6.4
Effect of the Sample Size
The larger the sample
size, the more nearly
normally distributed is
the population of all
possible sample means
Also, as the sample size
increases, the spread of
the sampling distribution
decreases
Chapter 6 Sampling
Distributions
How Large?
• How large is “large enough?”
• If the sample size n is at least 30, then for most
sampled populations, the sampling distribution of
sample means x is approximately normal
Refer to Figure 6.6 on next slide
– Shown in Fig 6.6(a) is an exponential (right
skewed) distribution
– In Figure 6.6(b), 1,000 samples of size n = 5
» Slightly skewed to right
– In Figure 6.6(c), 1,000 samples with n = 30
» Approximately bell-shaped and normal
• If the population is normal, the sampling distribution
of x is normal regardless of the sample size
Chapter 6 Sampling
Distributions
Example: Central Limit Theorem
Simulation
Chapter 6 Sampling
Distributions
Unbiased Estimates(无偏估计)
• A sample statistic is an unbiased point estimate of a
population parameter if the mean of all possible
values of the sample statistic equals the population
parameter
• x is an unbiased estimate of  because  x =
– In general, the sample mean is always an
unbiased estimate of 
– The sample median is often an unbiased estimate
of 
• But not always
Chapter 6 Sampling
Distributions
• The sample variance s2 is an unbiased
estimate of 2 if the sampled population is
infinite
– That is why s2 has a divisor of n–1
(if we used n as the divisor when estimating
2 , we would not obtain an unbiased
estimate)
However, s is not an unbiased estimate of 
– Even so, since there is no easy way to
calculate an unbiased point estimate of ,
the usual practice is to use s as an estimate
of 
Chapter 6 Sampling
Distributions
Minimum Variance Estimates
(最小方差估计)
• Want the sample statistic to have a small standard deviation
– All values of the sample statistic should be clustered
around the population parameter. Then, the statistic from
any sample should be close to the population parameter
• Given a choice between unbiased estimates, choose
one with smallest standard deviation
• Even though the sample mean and the sample median
are both unbiased estimates of , the sampling
distribution of sample means has a smaller standard
deviation than that of sample medians
Chapter 6 Sampling
Distributions
The sample mean is a minimum-variance
unbiased estimate (最小方差无偏估计) of

– When the sample mean is used to
estimate , we are more likely to obtain
an estimate close to  than if we used
any other sample statistic
– Therefore, the sample mean is the
preferred estimate of 
Chapter 6 Sampling
Distributions
Section 6.2 The Sampling Distribution
of the Sample Proportion(样本比例)
For a population of units, we select samples of size n,
and calculate its proportion p̂ for the units of the
sample to be fall into a particular category.
p̂ is a random variable and has its probability
distribution.
The probability distribution of all possible sample
proportions is called the sampling distribution of the
sample proportion
Chapter 6 Sampling
Distributions
the sampling distribution of
p̂
is
approximately normal, if n is large (meet the
conditions that np≥5 and n(1-p)≥5)
has mean  pˆ  p
p1  p 
has standard deviation  p̂ 
n
where p is the population proportion for the
category
Chapter 6 Sampling
Distributions
The Cheese Spread Case
• A food processing company developed a new cheese
spread spout which may save production cost. If only
less than 10% of current purchasers do not accept the
design, the company would adopt and use the new
spout.
• 1000 current purchasers are randomly selected and
inquired, and 63 of them say they would stop buying
the cheese spread if the new spout were used. So, the
sample proportion p̂ =0.063.
• To evaluate the strength of this evidence, we ask: if
p=0.1, what is the probability of observing a sample
of size 1000 with sample proportion p̂ ≦0.063?
Example 6.5
Chapter 6 Sampling
Distributions
• If p=0.10, since n=1000, np≥5 and n(1-p)≥5,
p̂ is approximately normal with
 pˆ  p  0.1,
p1  p 
 pˆ 
n
 0.094868,

0.063    



p 
P p  0.063 if p  0.1  P z 







p


0.063  0.10 

 P z 

0.094868 

 P z  3.90   0.001.

Chapter 6 Sampling
Distributions
• So, if p=0.1, the chance of observing at most
63 out of 1000 randomly selected customers
do not accept the new design is less than
0.001
• But such observation does occur. This means
that we have extremely strong evidence that
p≠0.1, and p is in fact less than 0.1
• Therefore, the company can adopt the new
design
Chapter 6 Sampling
Distributions
Chapter 7 Confidence
Intervals(置信区间)
 z-Based Confidence Intervals for a
Population Mean:  Known
 t-Based Confidence Intervals for a
Population Mean:  Unknown
 Sample Size Determination(样本
量计算)
 Confidence Intervals for a
Population Proportion
Section 7.1 z-Based Confidence
Intervals for a Population Mean
• The starting point is the sampling distribution(样本分
布) of the sample mean
– Recall from Chapter 6 that if a population is
normally distributed with mean  and standard
deviation , then the sampling distribution of x is
normal with mean  x =  and standard deviation
– Use a normal curve as a model of the sampling
distribution of the sample mean
• Exactly, because the population is normal
• Approximately, by the Central Limit Theorem for
large samples(大样本中心极限定理)
Chapter 6 Sampling
Distributions
• Recall the empirical rule, so…
– 68.26% of all possible sample means are
within one standard deviation of the
population mean
– 95.44% of all possible sample means are
within two standard deviations of the
population mean
– 99.73% of all possible sample means are
within three standard deviations of the
population mean
Chapter 6 Sampling
Distributions
The Car Mileage Case
Example 7.1
• Recall that the population of car mileages is normally
distributed with mean  and standard deviation  = 0.8
mpg
– Note that  is unknown and is to be estimated but
assumed that  = 31 mpg
• Taking samples of size n = 5, the sampling distribution
of sample mean mileages is normal with mean  = 
(which is
also unknown) and standard deviation
x
x 


0.8
 0.35777
n
5
• The probability is 0.9544
that
will be within plus or
minus 2 = 2 • 0.35777 = 0.7155
x of 
x
Chapter 6 Sampling
Distributions
The Car Mileage Case ＃2
• That the sample mean is within ±0.7155 of  is
equivalent to…
x will be such that the interval [ x ± 0.7115]
contains 
• Then there is a 0.9544 probability that x will be a
value so that interval [ x ± 0.7115] contains 
– In other words
P( x – 0.7155 ≤  ≤ x+ 0.7155) = 0.9544
– The interval [ x ± 0.7115] is referred to as the
95.44% confidence interval for 
Chapter 6 Sampling
Distributions
The Car Mileage Case ＃3
95.44% Confidence Intervals for 
• Three intervals
shown
• Two contain 
• One does not
Chapter 6 Sampling
Distributions
• According to the 95.44% confidence interval, we
know even before we sample that of all the possible
samples that could be selected …
• … There is 95.44% probability that the sample mean
that is calculated is such that the interval
[ x ± 0.7155] will contain the actual (but unknown)
population mean 
– In other words, of all possible sample means,
95.44% of all the corresponding intervals will
contain the population mean 
– Note that there is a 4.56% probability that the
interval does not contain 
• The sample mean is either too high or too low
Chapter 6 Sampling
Distributions
Generalizing
• In the example, we found the probability that 
is contained in an interval of integer multiples of
x
• More usual to specify the (integer) probability
and find the corresponding number of x
• The probability that the confidence interval will
not contain the population mean  is denoted by
a
– In the example, a = 0.0456
Chapter 6 Sampling
Distributions
Generalizing
Continued
• The probability that the confidence interval will
contain the population mean  is denoted by 1  a
– 1 – a is referred to as the confidence coefficient
– (1 – a)  100% is called the confidence level
– In the example, 1 – a = 0.9544
• Usual to use two decimal point probabilities for 1 – a
– Here, focus on 1 – a = 0.95 or 0.99
Chapter 6 Sampling
Distributions
General Confidence Interval
• In general, the probability is 1 – a that the
population mean  is contained in the interval
 

x  za 2 x   x  za 2

n


– The normal point za/2 gives a right hand tail area
under the standard normal curve equal to a/2
– The normal point - za/2 gives a left hand tail area
under the standard normal curve equal to a/2
– The area under the standard normal curve between
-za/2 and za/2 is 1 – a


Chapter 6 Sampling
Distributions
Chapter 6 Sampling
Distributions
z-Based Confidence Intervals for a
Mean with  Known
• If a population has standard deviation  (known),
• and if the population is normal or if sample size is
large (n  30), then …
• … a 1a)100% confidence interval for  is
x  za 2


 
  x  za 2
, x  za 2

n 
n
n

Chapter 6 Sampling
Distributions
95% Confidence Level
• For a 95% confidence level,
1 – a = 0.95
a = 0.05
a/2 = 0.025
• For 95% confidence, need the normal point z0.025
• The area under the standard normal curve between z0.025 and z0.025 is 0.95
• Then the area under the standard normal curve
between 0 and z0.025 is 0.475
• From the standard normal table, the area is 0.475 for
z = 1.96
• Then z0.025 = 1.96
Chapter 6 Sampling
Distributions
The Effect of a on Confidence
Interval Width
za/2 = z0.025 = 1.96
Chapter 6 Sampling
Distributions
za/2 = z0.005 = 2.575
95% Confidence Interval
The 95% confidence interval is

 
x  z0.025 x    x  1.96 
n



 
  x  1.96
, x  1.96

n
n

Chapter 6 Sampling
Distributions
99% Confidence Interval
• For 99% confidence, need the normal point
z0.005
• Reading between table entries in the
standard normal table, the area is 0.495 for
z0.005 = 2.575
• The 99% confidence interval is

 
x  z0.025 x    x  2.575 
n



 
  x  2.575
, x  2.575

n
n

Chapter 6 Sampling
Distributions
Example 7.2
Given:
The Car Mileage Case
= 31.5531 mpg
 = 0.8 mpg
n = 49
x
95% Confidence Interval: x  z 0.025   31 .5531  1.96 0.8
n
49
 31 .5531  0.224
 31 .33 , 31 .78 
99% Confidence Interval: x  z 0.005

 31 .5531  2.575
n
49
 31 .5531  0.294
 31 .26 , 31 .85 
Chapter 6 Sampling
Distributions
0.8
• The 99% confidence interval is slightly wider than the
95% confidence interval
– The higher the confidence level, the wider the
interval
• Reasoning from the intervals:
– The target mean mileage should be at least 31 mpg
– Both confidence intervals exceed this target
– According to the 95% confidence interval, we can
be 95% confident that the mileage is between 31.33
and 31.78 mpg
– So we can be 95% confident that, on average, the
mean mileage exceeds the target by at least 0.33
mpg and at most 0.78 mpg
Chapter 6 Sampling
Distributions
Section 7.2 t-Based Confidence
Intervals for a Population Mean
• If  is unknown (which is usually the case), we can
construct a confidence interval for  based on the
sampling distribution of
t
x 
s
n
• If the population is normal, then for any sample size n,
this sampling distribution is called the t distribution(t
分布)
Chapter 6 Sampling
Distributions
The t Distribution(t 分布)
• The curve of the t distribution is similar to that of the
standard normal curve
– Symmetrical and bell-shaped
– The t distribution is more spread out than the
standard normal distribution
– The spread of the t is given by the number of
degrees of freedom(自由度)
• Denoted by df
• For a sample of size n, there are one fewer
degrees of freedom, that is,
df = n – 1
Chapter 6 Sampling
Distributions
Degrees of Freedom and the
t-Distribution
As the number of degrees of freedom increases, the spread
of the t distribution decreases and the t curve approaches
the standard normal curve
Chapter 6 Sampling
Distributions
The t Distribution and Degrees of
Freedom
• For a t distribution with n – 1 degrees of freedom,
– As the sample size n increases, the degrees of
freedom also increases
– As the degrees of freedom increase, the spread of
the t curve decreases
– As the degrees of freedom increases indefinitely,
the t curve approaches the standard normal curve
• If n ≥ 30, so df = n – 1 ≥ 29, the t curve is very
similar to the standard normal curve
Chapter 6 Sampling
Distributions
t and Right Hand Tail Areas
• Use a t point denoted by ta
– ta is the point on the horizontal axis under the t
curve that gives a right hand tail equal to a
– So the value of ta in a particular situation depends
on the right hand tail area a and the number of
degrees of freedom
• df = n – 1
 a = 1 – a , where 1 – a is the specified
confidence coefficient
Chapter 6 Sampling
Distributions
Chapter 6 Sampling
Distributions
Using the t Distribution Table
• Rows correspond to the different values of df
• Columns correspond to different values of a
• See Table 7.3, Tables A.4 and A.20 in Appendix A and the
table on the inside cover
– Table 7.3 and A.4 gives t points for df 1 to 30, then for df =
40, 60, 120, and ∞
• On the row for ∞, the t points are the z points
– Table A.20 gives t points for df from 1 to 100
• For df greater than 100, t points can be approximated by
the corresponding z points on the bottom row for df = ∞
– Always look at the accompanying figure for guidance on
how to use the table
Chapter 6 Sampling
Distributions
Example 7.3 Find ta for a sample
of size n = 15 and right hand tail
area of 0.025
– For n = 15, df = 14
– a = 0.025
• Note that a = 0.025
corresponds to a confidence
level of 0.95
– In Table 7.3, along row
labeled 14 and under column
labeled 0.025, read a table
entry of 2.145
– So ta = 2.145
Chapter 6 Sampling
Distributions
t-Based Confidence Intervals for a
Mean:  Unknown
If the sampled population is normally distributed with
mean , then a 1a)100% confidence interval for  is
x  ta
s
2
n
ta/2 is the t point giving a right-hand tail area of a/2
under the t curve having n – 1 degrees of freedom
Chapter 6 Sampling
Distributions
Example 7.4
Debt-to-Equity Ratio
• Estimate the mean debt-to-equity ratio of the loan
portfolio of a bank
• Select a random sample of 15 commercial loan accounts
– Box plot is given in figure below
• Know: x = 1.34
s = 0.192
n = 15
• Want a 95% confidence interval for the ratio
• Assume all ratios are normally distributed but  unknown
Chapter 6 Sampling
Distributions
• Have to use the t distribution
• At 95% confidence,
• 1 – a = 0.95 so a = 0.05 and a/2 = 0.025
• For n = 15,
• df = 15 – 1 = 14
• Use the t table to find ta/2 for df = 14
• ta/2 = t0.025 = 2.145 for df = 14
• The 95% confidence interval:
x  t 0.025
s
 1.343  2.145
n
0.192
15
 1.343  0.106
 1.237 ,1.449 
Chapter 6 Sampling
Distributions
Section 7.3 Sample Size
Determination
If  is known, then a sample of size
 za 2
n  
 E



2
Letting E denote the desired margin of error, so that x
is within E units of , with 100(1-a)% confidence.
Chapter 6 Sampling
Distributions
If  is unknown and is estimated from s, then a sample
of size
 ta 2 s 

n  
 E 
2
so that x is within E units of , with 100(1-a)%
confidence. The number of degrees of freedom for the
ta/2 point is the size of the preliminary sample minus 1
Chapter 6 Sampling
Distributions
Example 7.5
Car Mileage Case
Given: x = 31.5531 mpg
s = 0.7992 mpg
n = 49
t- based 95% Confidence Interval:
x  t0.025
s
0.7992
 31.5531  2.0106
n
49
 31.5531  0.2296
 31.32, 31.78
where ta/2 = t0.025 = 2.0106 for df = 49 – 1 = 48
degrees of freedom
Note: the error bound B = 0.2296 mpg, within the
maximum error of 0.3 mpg
Chapter 6 Sampling
Distributions
Section 7.4 Confidence Intervals for a
Population Proportion
If the sample size n is large*, then a 1a)100%
confidence interval for p is
p̂  z a 2
p̂1  p̂ 
n
* Here n should be considered large if both
n  pˆ  5 and n  1  pˆ   5
Chapter 6 Sampling
Distributions
Example 7.6
Phe-Mycin Side Effects
Given: n = 200, 35 patients experience nausea.
35
p̂ 
 0.175
200
Note:
npˆ  200  0.175  35
n1  pˆ   200  0.825  165
so both quantities are > 5
For 95% confidence, za/2 = z0.025 = 1.96 and
p̂  z a 2
p̂1  p̂ 
0.175  0.825
 0.175  1.96
n
200
 0.175  0.053
 0.122 , 0.228 
Chapter 6 Sampling
Distributions
Determining Sample Size for
Confidence Interval for p
A sample size
 za 2
n  p 1  p 
 E



2
will yield an estimate p̂ , precisely within E units of p,
with 100(1-a)% confidence
Note that the formula requires a preliminary estimate of
p. The conservative value of p = 0.5 is generally used
when there is no prior information on p
Chapter 6 Sampling
Distributions
A Comparison of Confidence
Intervals and Tolerance Intervals
A tolerance interval contains a specified percentage of
individual population measurements
• Often 68.26%, 95.44%, 99.73%
A confidence interval is an interval that contains the
population mean , and the confidence level expresses
how sure we are that this interval contains 
• Often confidence level is set high (e.g., 95% or 99%)
– Because such a level is considered high enough to
provide convincing evidence about the value of 
Chapter 6 Sampling
Distributions
Example 7.7
Car Mileage Case
Tolerance intervals shown:
[
x
[
x
± s] contains 68% of all individual cars
± 2s] contains 95.44% of all individual cars
[ x ± 3s] contains 99.73% of all individual cars
The t-based 95%
confidence interval for 
is [31.32, 31.78], so we
can be 95% confident
that  lies between 31.23
and 31.78 mpg
Chapter 6 Sampling
Distributions
Summary: Selecting an Appropriate
Confidence Interval for a Population Mean
Chapter 6 Sampling
Distributions