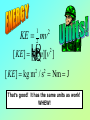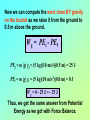Download presentation source

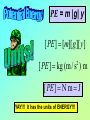
Wenesday, September 30, 1998
Chapter 5: Kinetic and Potential Energy
Conservative vs Nonconservative
Forces
• What’s the best thing about physics class?
• What’s the worst thing?
• If there was one thing you could change, what
would it be?
PLEASE TURN IN TODAY!
mas  Fs  m(v  v )
1
2
2
Each term on the right-hand-side
of this equation is called a “kinetic
energy” term.
2
0
KE  mv
1
2
And now we can rewrite work as a change
in kinetic energy:
Wnet  KE  KE  KE0  mv  mv
1
2
2
1
2
2
0
2
KE  mv
L
2
1O
[ KE ]  M
[
m
][
v
]
P
N2 Q
1
2
2
[ KE ]  kg m / s  Nm  J
2
2
That’s good! It has the same units as work!
WHEW!
Although we’ve derived this relationship
between work and kinetic energy for the
special case of a constant applied force
(I.e., constant acceleration), it turns out
to be generally true, regardless of whether
or not the force is constant!
The NET WORK done on an object is equal
to its change in KINETIC ENERGY.
Let’s go back to the bucket
example…We saw that a man
raising a 5 kg bucket through
0.5 m at constant velocity does
an amount of work
W = 25 J
But if the NET WORK done on the bucket equals
the change in kinetic energy of the bucket, then
1
2
2
Wnet  KE  m(v  v0 )  0
2
What’s the deal?
Solution: Although the man does
25 J of work lifting the bucket, the
force of gravity (acting in the
opposite direction) does 25 J of
work in the opposite direction.
Wnet = Wman + Wg = 25 J - 25 J = 0
The key to unlocking this conundrum was
that we need to calculate the
NET WORK DONE ON THE BUCKET!!!
(Not that done by the man or by gravity alone!)
If we look at the free-body-diagram for
the bucket, we see that there are two
forces acting on it:
The two forces are
equal in magnitude
and oppositely directed
(in this case) since
we know that the
velocity of the
bucket is constant!
3rd Law Pair????
Force
of man
weight
Something should be bugging us about this
last problem still...
Afterall, we certainly changed the position of
the bucket. And if we let go, it would fall back
to the ground.
The higher we raise the bucket, the faster its
speed when it does hit the ground.
Ladies and Gentlemen….INTRODUCING:
Because we are in the space strongly
influenced by the Earth’s gravity, we
call this the gravitational potential energy.
Consider the force gravity exerts on the bucket
as we move it from the ground to a height of
0.5 m at constant velocity.
Fg = m g = (5 kg)(-10 m/s2) = -50 N
W = Fs s = Fg (yf - yi)
= (-50 N)(0.5 m - 0.0 m) = -25 J
We DEFINE gravitational potential energy
PE = m |g| y
PE = m |g| y
[ PE ]  [m][ g][ y]
[ PE ]  kg (m / s ) m
2
[ PE ]  N m  J
YAY!!! It has the units of ENERGY!!!
Now we can compute the work done BY gravity
on the bucket as we raise it from the ground to
0.5 m above the ground.
Wg = PEi - PEf
PEf = m |g| yf = (5 kg)(10 m/s2)(0.5 m) = 25 J
PEi = m |g| yi = (5 kg)(10 m/s2)(0.0 m) = 0 J
Wg = 0 - 25 J = - 25 J
Thus, we get the same answer from Potential
Energy as we got with Force Balance.
We are free to define the origin of our
y-coordinate at any point above the Earth’s
surface (or below it) that we find convenient -since the work done only depends upon the
CHANGE IN HEIGHT!
Potential Energy, like kinetic energy is a scalar.
Our definition of gravitational potential energy
can only be applied near the Earth’s surface.
So…WHY DO we call it POTENTIAL energy?
If this guy holds the 5 kg bucket
still 0.5 m off the ground, what
is the bucket’s Kinetic energy?
Potential energy?
What happens if he drops
the bucket?
0.5 m
What are the kinetic and
potential energies when
the bucket hits the ground?
What do we notice about the initial
potential energy and the final kinetic
energy of our guy & the bucket?
PEi = KEf
We’re going to generalize now, but you should
be able to prove this to yourself through a few
practice problems.
KEi + PEi = KEf + PEf
We call
KE + PE
The TOTAL
MECHANICAL
ENERGY
KE + PE = constant!
The total mechanical energy of any isolated
system of objects remains constant if the
objects interact only through conservative
forces.