Download sect. 1-4

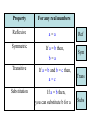
Section 1.4
Solving Equations
The Language of algebra provides a way
to translate word expressions into
mathematical equations
1) Write each equation as I read them
a)
b)
c)
Def: Variables are used to represent
numbers that are not known.
Def: An open sentence that states that two
mathematical expressions are equal is called
an equation.
Def: To solve an equation, you find the
values of the variable that make the
equation true. Those values are called
solutions.
In order to solve an equation we may
only use appropriate properties.
Property
Reflexive
Symmetric
For any real numbers
a=a
If a = b then,
b=a
Transitive
If a = b and b = c then,
a=c
Substitution
Ref
Sym
Trans
If a = b then,
you can substitute b for a
Subs
Properties of Equality:
Addition Property of Equality: if a = b then:
a+c=b+c
Subtraction Property of Equality: if a = b then:
a-c=b-c
Multiplication Property of Equality: if a = b then:
a*c = b*c
Division Property of Equality: if a = b then:
a/c=b/c
Any restrictions here?
You can’t divide by 0
c≠0
2.) Solve and name the property
a.)
b)
x+9=6+9
28 = 6y+4
c) r +(6+9) = 32
3.) Solve and name the property:
3(2a + 25) - 2(a - 1) = 78
Solve using the problem-solving plan
1. Read the problem
2. Plan the solution
3. Solve the problem
4. Check to see if answer is reasonable
Homework
Page 31
Problems:
#19 – 30 all, 31 - 45 (odd), 57 and 63