Download Chapter 11

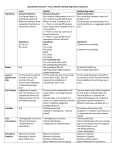
Chapter 11
Measuring Item
Interactions
McGraw-Hill/Irwin
© 2004 by The McGraw-Hill Companies, Inc. All rights reserved.
Identifying Variable Types
and Forms
• Direction of Causality
• Independent variables influences or affects the
other
• Dependent variable is the one being influenced or
affected
• Form of the Variables
• All nominal variables are categorical
• Ordinal, interval, and ratio variables are continuous
in form
• Continuous variables may be recoded or treated as
categorical
• If so, they must constitute a limited number of
categories
11-2
Measures of Association
Continuous Categorical
Dependent
Independent
Categorical
Continuous
CrossTabulation
Discriminant
Analysis
Analysis of
Variance
Regression
Analysis
---------------
---------------
Chi-Square
F-Ratio
Paired T-Test
Value of t
F-Ratio
F-Ratio
Correlation
Probability of r
11-3
When To Use CrossTabulation
• Both variables are categorical (in the form of
categories), rather than continuous
• The object is to see if the frequency or percentage
distribution breakdown for one variable differs for each
level of the other
• One variable is used to define the rows of the matrix
and the other to define the columns
• If the distribution of each row or each column is
proportional to the row or column totals, the two
variables are not significantly related
11-4
Expected Cell Frequencies
• The lowest expected cell frequency for the table
must be 5 or more
• Look down the row totals and circle the lowest row total
• Look across the column totals and circle the lowest
column total
• Divide the lowest row total by the grand total for the
entire table
• Multiply this value by the lowest column total to get the
lowest expected cell frequency
• If it is less than five, combine the row or the column
with another and recalculate the lowest cell frequency
11-5
The Cross-Tabulation Table
• Table is symmetrical: Either variable can be listed on the
rows or columns
• There need not be a dependent and an independent
variable
• If there is a dependent variable, it's often best to have it
define the rows
• If the dependent variable defines the rows, column
percentages work best
• Each percentage can then be compared to the total row
percentages
11-6
Perfectly Proportional
Cross-Tab Table and Graph
One
25
25
Row
Total
50
Two
25
25
50
Col.
Total
50
50
100
One Two
Chi Sq. = 0
Sig. = 1.0000
Col. 1
Col. 2
Row
One
Row
Two
0
10 20 30 40 50
11-7
Slightly Disproportional
Cross-Tab Table and Graph
One
30
20
Row
Total
50
Two
20
30
50
Col.
Total
50
50
100
One Two
Chi Sq. = 4
Sig. = 0.0455
Col. 1
Col. 2
Row
One
Row
Two
0
10 20 30 40 50
11-8
Highly Disproportional
Cross-Tab Table and Graph
One
40
10
Row
Total
50
Two
10
40
50
Col.
Total
50
50
100
One Two
Chi Sq. = 36
Sig. = 0.0000
Col. 1
Col. 2
Row
One
Row
Two
0
10 20 30 40 50
11-9
Perfectly Disproportional
Cross-Tab Table and Graph
One
50
0
Row
Total
50
Two
0
50
50
Col.
Total
50
50
100
One Two
Chi Sq. = 100
Sig. = 0.0000
Col. 1
Col. 2
Row
One
Row
Two
0
10 20 30 40 50
11-10
Significance of Chi Square
• The statistical significance of the relationship depends
on the probability of disproportions by row or by column
if the distributions in the population were actually
proportional
• The actual probability is based on the value of Chi-square
and the degrees of freedom
• The number of degrees of freedom equals number of
rows minus one times number of columns minus one (R1) X (C-1)
• The probability can be read from a table, but it is usually
generated by the analysis program
11-11
Ways to Describe the Statistical
Significance of Cross-Tabs
• What is the probability this much difference in the
proportions from row to row or column to column would
result only from sampling error if the proportions were
were equal in the population?
• If the proportions from row to row or column to column
were the same in the population, what are the odds that a
sample of this size would show this much difference in the
proportions for the sample?
• What is the probability that proportions from row to row
or column to column would be this different by chance,
purely because of sampling error, if the proportions in the
population were actually the same?
11-12
Analysis of Variance
(ANOVA)
• Objective
• To determine if the means of two or more variables are
significantly different from one another.
• Independent Variable
• Nominal level data in the form of two or more categories.
• Dependent Variable
• Interval or ratio level data in continuous form.
• Requirements
• Dependent variable must be near-normally distributed
and the variance within each category must be
approximately equal.
11-13
Variance Not Homogeneous
• Dispersion in the red category
is greater than in the green
ANOVA
11-14
Skewed Distributions
ANOVA
• The distributions are asymmetrical
(skewed to one side)
11-15
ANOVA or Paired T-Test?
• ANOVA requires that the data points are independent.
(From different cases)
• ANOVA will measure significance of differences among
more than two means or categories
• Paired T-Tests require that the data points are paired
(That they come from the same case)
• Paired T-Tests can measure the significance of difference
between only two means or variables
11-16
ANOVA - Difference Not
Significant
• Mean a and b are very close.
• Overlapping area is very large.
acb
11-17
ANOVA - Difference
Probably Significant
• Mean a and b are far apart
• Overlapping area is rather small
a
c
b
11-18
The ANOVA Table
Source
Between groups
Within groups
Combined
•
•
•
•
•
•
S.S.
100
180
280
d.f.
1
9
10
M.S.
100
20
F
5.00
P
0.00
SOURCE - The source of the variance value
S.S. - Sums of Squared deviations from a mean
d.f. - Degrees of freedom related to variance
M.S. -Mean Squares or S.S. divided by d.f.
F - The ratio of M.S.Between over M.S.Within
P - The probability of this value of the F-ratio
11-19
ANOVA Terms — Sums of
Squares
Source
Between groups
Within groups
Combined
S.S.
100
180
280
d.f.
1
9
10
M.S.
100
20
F
5.00
P
0.00
• S.S.—The sum of squared deviations of each data point
from some mean value
• Within groups—The total squared deviation of each
point from the group mean
• Combined—The total squared deviation of each data
point from the grand mean
• Between groups—The difference between S.S.
combined and S.S. within groups
11-20
ANOVA Terms — Degrees of
Freedom
Source
Between groups
Within groups
Combined
S.S.
100
180
280
d.f.
1
9
10
M.S.
100
20
F
5.00
P
0.00
• d.f.—The number of cases minus some "loss" because
of earlier calculations.
• Within groups d.f.—The total number of cases minus
the number of groups.
• Combined d.f.—Equal to the total number of cases
minus one.
• Between groups d.f.—Equal to the total number of
groups minus one.
11-21
ANOVA Terms — Mean
Squares & F-Ratio
Source
Between groups
Within groups
Combined
S.S.
100
180
280
d.f.
1
9
10
M.S.
100
20
F
5.00
P
0.00
• M.S.—the sums of squares (S.S.) divided by the
degrees of freedom (d.f.).
• F—the ratio of mean squares between groups to the
mean squares within groups.
11-22
Ways to Describe the Statistical
Significance of ANOVA
• What is the probability that this much of a difference
between these sample mean values would result due to
sampling error if the means for the groups in the
population were equal?
• If the group means in the population as a whole were the
same, what are the odds that a sample of this size would
show this much difference in the sample group means?
• What is the probability that the sample group means
would be this different by chance, purely because of
sampling error, if the group means in the population were
actually the same?
11-23
Correlation Analysis
• Objective
• To determine degree and significance of relationship
between a pair of continuous variables
• Causality
• The analysis does not assume that one variable is
dependent on the other. If A is correlated with B:
•
•
•
•
A
B
A
C
may be causing B
may be causing A
and B may be interacting
may be causing A and B
11-24
Correlation Analysis
• Requirements
• Both variables must be continuous and obtained
from an interval or a ratio scale
• Non-Parametric Correlation
• Both variables must be continuous but one or both
may be only ordinal scale level
11-25
Regression Analysis
• Objective
• To determine if variable X has a significant effect
on variable Y
• Independent Variable
• X must be continuous, interval or ratio level data
• Dependent Variable
• Y must be continuous, interval or ratio level data
11-26
Regression Analysis
Requirements
• The data plot must be linear
• The data plot must be in a straight line or
very nearly so
• The data plot must be homoskedastic
• The vertical spread must be about the same
from left to right
11-27
Unacceptable Heteroskedastic
Regression Plot
• Typical funnel-shaped plot
• The scatterplot must be homoskedastic
• Variance must be approximately the same
Regression
11-28
Unacceptable Curvilinear
Regression Plot
• The scatterplot must be linear
• A runs test will reveal nonlinearity
• It gives probability of consecutive signs
Regression
+
+
+
-
+
+
+
+
+
+
11-29
Unacceptable Quadratic
Regression Plot
• Two linear segments with one bend
• Three segments, two bends is cubic, etc.
• Regression must be limited to one range
Regression
11-30
The Regression Scatterplot
• Independent variable X on the horizontal axis
• Dependent variable Y on the vertical axis
• Regression equation: Y = a + bX
Strong Relationship
Weak Relationship
11-31
Regression Plot and
Regression Table
100
75
50
25
0
0
20
Corr. (r)
.93784
R-Square
.87954
Intercept (A) 88.90818
Slope (B)
-0.96698
Source
Regression
Residual
40
60
80
100
Regression Table
N of cases25
S.E. Est. 8.76849
S.E. of A 3.64090
S.E. of B 0.07462
Analysis of Variance
S.S.
d.f.
M.S.
12911.77
1
12911.77
1768.38
23
76.89
Missing 0
Sig. R 0.0000
Sig. A 0.0000
Sig. B 0.0000
F Ratio
167.9332
F Prob.
0.0000
11-32
Regression Coefficients
Corr. (r)
.93784
R-Square
.87954
Intercept (A) 88.90818
Slope (B)
-0.96698
Regression Table
N of cases25
S.E. Est. 8.76849
S.E. of A 3.64090
S.E. of B 0.07462
Missing 0
Sig. R 0.0000
Sig. A 0.0000
Sig. B 0.0000
• Corr. (r) — The coefficient of correlation
• R-Square — The coefficient of determination
• The percentage of variance in Y explained by knowing X
• Intercept (A) — Value of Y if X is zero
• Slope (B) — The rise over the run
• Regression equation — Y = a + bX
11-33
Regression Coefficients
Corr. (r)
.93784
R-Square
.87954
Intercept (A) 88.90818
Slope (B)
-0.96698
Regression Table
N of cases25
S.E. Est. 8.76849
S.E. of A 3.64090
S.E. of B 0.07462
Missing 0
Sig. R 0.0000
Sig. A 0.0000
Sig. B 0.0000
• S.E. Estimate — StandardY based on the value of X
• S.E. of the estimate based on the regression equation
• S.S. Regression — Sum of squared deviations of each
data point from the regression line
• S.S. Residual — The difference between S.S. total
(around the mean of Y) and S.S. Regression
11-34
Ways to Describe the Statistical
Significance of Regression
• What is the probability this much variance in the values
of the dependent variable would would be “explained” by
the values of the independent variable, only because of
sampling error, if the two variables were unrelated in the
population?
• If these two variables were actually independent of one
another in the population, what are the odds that this size
sample would show this much of a relationship?
• What is the probability that the values of X would explain
this much variance in Y, purely by sampling error, if X and
Y were unrelated to one another in the entire population?
11-35
End of
Chapter 11
McGraw-Hill/Irwin
© 2004 by The McGraw-Hill Companies, Inc. All rights reserved.