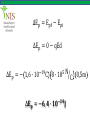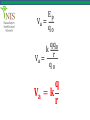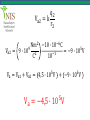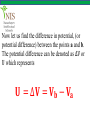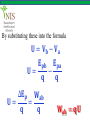Download Electric potential energy

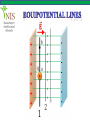
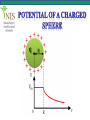
The 21st of JANUARY
Teacher:
Altynbekov Ayan
• Electric potential energy
• Electric potential
• Potential difference (Voltage)
• The relationship between potential
difference and electric field
• Equipotential lines
• Potential of a charged sphere
• Motion of charged particles in a
uniform electric field
In each area of physics there are interesting
similarities between the laws of physics.
Before introducing electric potential energy,
let us remember gravitational potential energy,
from mechanics.
When an object is raised in the air to a certain
height, work is done against the gravitational
force.
The work done is stored as
gravitational potential
energy in the object-Earth
system. When we release
the object, it accelerates
downwards changing its
potential energy into kinetic
energy.
In this process the gravitational force is doing
work. The work done by the gravitational force
is positive as the object falls downwards and
the gravitational potential energy decreases. So,
the work done by Fg as the object falls from h1
to h2 is equal to the negative of the change in
gravitational potential energy.
Wg = Fg h = mgh2 − mgh1
𝐖𝐠 = −∆𝐄𝐩
So the change in potential energy of an object
to the negative of the work done by the
gravitational force.
As the object moves in the same direction as
the gravitational field it loses potential energy.
This is an analogy for the electrical case.
Suppose a positive point charge of +q, is placed
in a uniform electric field produced by two
oppositely charged parallel plates, as in figure.
The charge +q has its maximum electric
potential energy just near the positive plate at
point 1.
When the charge is released, it is moved by the
Electric field. Its electric potential energy
decreases as it changes into kinetic energy.
The electric force does positive work, W, on
the charge because the electric force, F = qE
and the distance, d are in the same direction.
The work done by the electric forces is equal
to the negative of the change in potential
energy of the charge.
W = −∆Ep
qEd = − Ep2 − Ep1
qE d1 − d2 = − Ep2 − Ep1
qEd1 − qEd2 = Ep1 − Ep2
The equation shows us that the difference
between initial and final values of (qEd) is
equal to the difference between initial and final
values of Ep .
Hence the electric potential energy of charge q
in a uniform field is
𝐄𝐩 = 𝐪𝐄𝐝
A proton is released from rest in a uniform
electric field of magnitude 8 ∙ 105 N C, as shown
in the figure. Find the change in potential
energy of a proton and its speed
just before striking the negative
plate. The distance between the
plates is 50 cm.
q = 1,6 ∙ 10−19 C
m = 1,67 ∙ 10−27 kg
Solution
The electric field in this region is so strong that
we can ignore gravitation. The proton moves
from a point of high potential energy to a point
of low potential energy. (Because it moves in
the direction of the electric field)
∆Ep = Epf − Epi
∆Ep = 0 − qEd
−19
∆Ep = − 1,6 ∙ 10
5N
C 8 ∙ 10
∆𝐄𝐩 = −𝟔, 𝟒 ∙ 𝟏𝟎
−𝟏𝟒
𝐉
C 0,5m
We can find the speed of the proton using the
principle of conservation of energy
Epi + Eki = Epf + Ekf
mv 2
qEd + 0 = 0 +
2
v=
2qEd
=
m
2 6,4 ∙ 10−14 J
7
=
2,8
∙
10
m/s
−27
1,67 ∙ 10 kg
Let’s go a step further. The gravitational
potential energy between any two masses m1
and m2 is given by
m1 m2
Ep = −G
r
The negative sign is due to the fact that the
gravitational force is always attractive.
Let’s use this analogy between gravitational force
and electric force. Consider two point charges q1
and q2 . The electric potential energy of charges
q1 and q2 will be
q1 q 2
Ep = k
r
q1 q 2
Ep = k
r
In this expression electric potential energy can
be both negative and positive, depending on the
sign of the charges. It is positive if the charges
are of the same sign and negative if the charges
are of opposite signs. This is the case for the
electric force since it can be both attractive and
repulsive.
Find the potential energy of a system of point
charges of q1 = 20μC and q2 = −10μC when
they are r1 = 20cm apart. How does the potential
energy change if we separate charges to a distance
of r2 = 40cm.
Solution
Their potential energy when they are r1 = 20cm
apart is
2
−6 C −10 ∙ 10−6 C
q1 q 2
N
∙
m
20
∙
10
Ep = k
= 9 ∙ 109
∙
2
r1
C
0,2m
Ep = −9J
Their potential energy when they are r2 = 40cm
apart is
2
−6 C −10 ∙ 10−6 C
q1 q 2
N
∙
m
20
∙
10
Ep = k
= 9 ∙ 109
∙
2
r2
C
0,4m
Ep = −4,5J
Their potential energy has increased (Ep2 > Ep1 )
because the potential energy of unlike charges
increases as we separate them.
Three charges are placed at the corners of an
equilateral triangle, as shown in the figure.
a) What is the electrical energy of charge +q at
point B?
b) What is the electrical potential of the system?
Solution
A) The potential energy of charge +q at point B is
equal to the algebraic sum of the potential
energies due to each charge then
q −2q
Ep = kq
+
r
r
q2
Ep = −k
r
B) The potential energy of the system is the sum of
the potential energies of each pair of charges.
Therefore,
qq q −2q
q −2q
Ep = k
+
+
r
r
r
3q2
Ep = −k
r
This energy is also equal to the work done by the
field in bringing the given charges to the points A,B
and C.
To define a quantity which is independent of test
charge, q0 we divided force, F, by the magnitude
of the test charge, q0 . We found a quantity that
characterizes the electric force of the charge at
that point; electric field.
A similar definition can be used to express electric
potential energy in a more appropriate way.
Suppose that a charge, q, is fixed at any point in
space. When a test charge, q0 , is near charge q, as
shown in figure, the electric potential energy of
the system is given by
qq0
Ep = k
r
Now we define a new physical quantity that
characterizes the electric potential energy at a
point near charge, q. This is called electric
potential and is defined as; the electric energy
per unit charge. The electric potential at a point
a, where the test charge was placed is denoted by
Va .
Ep
Va =
q0
qq 0
k
r
Va =
q0
𝐪
𝐕𝐚 = 𝐤
𝐫
Note that the electric potential of the
charge q at point a is independent of
the test charge. Electric potential is a
scalar quantity. The SI unit of electric
potential is the Joule/Coulomb and is
given the special name of the Volt, (V).
Two charges of 5μC and −10μC are placed at the
corners of an equilateral triangle of side length 10
cm. Determine the electric potential at point a.
Solution
The net electric potential at point a is the
algebraic sum of electric potentials due to both
charges.
Va1
Va1
Nm
= 9 ∙ 10
C2
9
q1
=k
r1
2
−6
5 ∙ 10 C
5
=
4,5
∙
10
V
10−1
Va2
Va2
q2
=k
r2
2
−6
Nm
−10
∙
10
C
9
5
= 9 ∙ 10
=
−9
∙
10
V
2
−1
C
10
Va = Va1 + Va2 = 4,5 ∙ 105 V + −9 ∙ 105 V
5
Va = −4,5 ∙ 10 V
Electric potential energy, just like other types of
potential energies, depends on a reference point
chosen to be zero potential. Instead of potential
energy or potential at a point, in practice the
difference in potential between two points is
important and measurable.
Suppose a positive charge, +q is placed at point a
in a uniform electric field, E as shown in figure.
As the charge is moved from the initial point a to
the final point b, by an external force, it does
positive work against the electric force. The
electric potential energy of the charge increases.
We can write
𝐖𝐚𝐛 = ∆𝐄𝐩
Now let us find the difference in potential, (or
potential difference) between the points a and b.
The potential difference can be denoted as ∆V or
U which represents
𝐔 = ∆𝐕 = 𝐕𝐛 − 𝐕𝐚
Not that Vb is the potential at the final point b and
Va is the potential at the initial point a.
𝐄𝐩𝐛
𝐕𝐛 =
𝐪
𝐄𝐩𝐚
𝐕𝐚 =
𝐪
Where Epa and Epb are the electric potential
energies at the points a and b.
By substituting these into the formula
𝐔 = 𝐕𝐛 − 𝐕𝐚
𝐄𝐩𝐛 𝐄𝐩𝐚
𝐔=
−
𝐪
𝐪
∆𝐄𝐩 𝐖𝐚𝐛
𝐔=
=
𝐪
𝐪
𝐖𝐚𝐛 = 𝐪𝐔
𝐖𝐚𝐛
𝐔 = 𝐕𝐛 − 𝐕𝐚 =
𝐪
Potential difference between two points is defined
as, the work done on a positive charge by external
forces, divided by the magnitude of the charge.
When a positive charge moves in the direction of
the electric field, electric forces do positive work
and the electric potential energy of the charge
decreases.
The SI unit of potential difference is the Volt (V).
A particle of charge q = 5μC is displaced from a
point at potential 700V to a point of potential 50V.
What work is done by the external force, Wext
and the electric force We ?
Solution
The charge is displaced from a point of high
potential to a point of low potential. The work
done by the external force is
Wext = q Vb − Va
Wext = 5 ∙ 10−6 C 50V − 700V
−𝟑
𝐖𝐞𝐱𝐭 = −𝟑, 𝟐𝟓 ∙ 𝟏𝟎
𝐉
Thus, the work done by the electric force is the
opposite of Wext
We = 3,25 ∙ 10−3 J
This means that the potential energy of the charge
decreases, if it is displaced parallel to the
direction of the electric field.
The electric field between two
parallel metal plates which are
oppositely charged is almost
uniform, especially when the
distance between the plates is small. We can
charge the plates oppositely by connecting them
to the terminals of a battery.
Suppose that a positive charge +q is placed at a
point just near the positive plate. If the distance
between the plates is d, the electric potential
energy of the charge is given by
𝐄𝐩 = 𝐪𝐄𝐝
For simplicity, we choose the potential at the
negative plate to be zero, thus the electric
potential energy of the charge at the negative plate
will be zero. We know that potential difference is
given by
𝐖𝐛𝐚 𝐄𝐩 − 𝟎 𝐪𝐄𝐝
𝐔=
=
=
𝐪
𝐪
𝐪
𝐔 = 𝐄𝐝
The formula can be expressed in terms of electric
field, E as
𝐔
𝐄=
𝐝
The SI unit of electric field can be expressed in
terms of the unit of voltage
𝐍
𝐕
𝟏 =𝟏
𝐂
𝐦
Suppose a charge q is displaced
from point a to point b along a line
perpendicular to the electric field.
The work done by the electric force
is zero because force and distance
are perpendicular. So if any charge
is moved along a line (or surface in
three dimensions) perpendicular to
the electric field, the work done is
zero. This means that the points on this line (or
surface) are all at the same potential. When we
move a charge on line 2, work done is also zero.
The potential energy of the charge remains constant
Ep = qEd .
So lines 1, 2 and 3 are called equipotential lines
(or surfaces).
When a conducting sphere is charged, its charge,
q is distributed uniformly over its surface area.
Suppose that a test charge, q0 is moved from a
point a on the sphere to another point b on the
sphere. The work done to move the charge, q0
does not depend on the path between the points a
and b.
Assume that the charge is moved from a to b
inside the sphere along the path, d. The work done
is given by
Wba = q 0 Uba
Wba = q 0 Vb − Va
Vb and Va are at the same potentials because they
are on the same equipotential surface. So, the work
done is zero, Wba = 0. This shows that inside the
sphere, the potential at every point is the same and
is equal to the potential at the surface.
𝐪
𝐕=𝐤
𝐑
When a particle of charge, q and mass, m is
released in a uniform electric field, it experiences
an electric force as in figure. If the only force
acting on it is the electric force we can use
Newton’s law in the form
𝐅𝐞 = 𝐦𝐚
𝐅𝐞 = 𝐦𝐚
q E = ma
qE
a=
m
The magnitude of the acceleration of the particle is
constant. Its direction is the same as the electric
field direction if the charge is positive and its
direction is opposite the electric field direction if
the charge is negative.
Note that we have ignored the gravitational
force acting on the particle.
http://moodle.nis.edu.kz
[email protected]
Electricity and Magnetism, Zambak publishing,
Ahmet Aki, Salim Gur