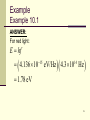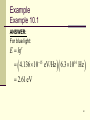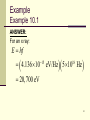Download Chapter 10 Notes

Chapter 10
Atomic Physics
The quantum hypothesis
 By the end of the 1800’s, physics had made
significant progress.

Some physicists feared “that all of their
questions might soon be answered.”
 But some problems defied solution:



blackbody radiation,
photoelectric effect, and
atomic spectra.
2
Blackbody radiation
 Everything around you is constantly emitting
electromagnetic (EM) radiation.
 A perfectly “black” body would:


absorb all light and other EM radiation incident
upon it, and
be a perfect emitter of EM radiation.
 Such an object is called a blackbody.
 The EM radiation emitted by it is called
blackbody radiation (BBR).
3
Blackbody radiation, cont’d
 The characteristics of BBR emitted at a
particular frequency can be illustrated with a
graph of the radiation intensity versus
wavelength.

Such a graph is
called a
blackbody
radiation curve.
4
Blackbody radiation, cont’d
 This graph illustrates two important ways that
BBR changes when the temperature of the
body is increased.

More energy is
emitter per
second at each
wavelength of
EM radiation,
and
5
Blackbody radiation, cont’d

The wavelength at which the most energy is
emitted per second shifts to smaller values.

In other words, the peak of the BBR curve moves
toward smaller
wavelengths
as the
temperature
increases.
6
Blackbody radiation, cont’d
 The principles of electromagnetism explain
some of this:

A blackbody emits radiation since the atoms
and molecules are continually oscillating.

Recall that a vibrating electric charge emits EM
radiation.
 But some things could not be answered.

An explicit explanation of the two mentioned
features could not be resolved.
7
Blackbody radiation, cont’d
 A “solution” was devised in 1900 by the
German physicist Max Planck.

He developed a mathematical equation that
accurately fit the blackbody radiation curve.


This gives the correct formula but no physical
insight.
He then developed a model that would
produce the desired equation.

He did not believe the model was physical even
though it gave the right answer.
8
Blackbody radiation, cont’d
 He proposed that an oscillating atom in a
blackbody can only exchange certain fixed
values of energy.

It can have zero energy, or a particular energy
E, or 2E, or 3E, ….
 This means that the energy of each atomic
oscillator is quantized.
 The energy E is called the fundamental
quantum of energy for the oscillator.
9
Blackbody radiation, cont’d
 The idea of quantization can be illustrated
with the following figure.


On the right, the cat can rest at any height
above the floor.
On the left, the cat can only rest at certain
heights above the floor.
10
Blackbody radiation, cont’d
 This means that:


The left cat’s potential energy can only
assume certain values.
The right cat’s potential energy can assume
any value.
11
Blackbody radiation, cont’d
 Planck determined that the basic quantum of
energy is proportional to the oscillator’s
frequency:
E  hf

h  6.63 10
34
J×s
The constant h is called Planck’s constant.
 The allowed energies are then
E  0, or E  hf , or E  2hf , ...
12
The photoelectric effect
 The second phenomenon defying classical
explanation was the photoelectric effect.
 The effect occurs when certain EM radiation
illuminates a metal then electrons are ejected
from the metal.
 The EM wave
gives energy to
the electrons
and allows them
to escape the
metal.
13
The photoelectric effect, cont’d
 Albert Einstein extended Planck’s quantum
hypothesis to solve this problem.
 Planck suggested that light is emitted in
discrete bundles of energy.

Einstein took this one step farther.
 He proposed that the light remains in these
bundles of energy and is absorbed in this
form.
14
The photoelectric effect, cont’d
 He suggested that the amount of energy in
one bundle of energy of frequency f is
E  hf
 This allows us to visualize the wave as being
composed of individual particles of energy,
now called photons.
15
The photoelectric effect, cont’d
 This allowed all aspects of the photoelectric
effect to be understood.


Higher-frequency light ejects electrons with
more energy because each photon has more
energy to impart to the electron.
Bright light simply means more photons strike
the metal so that more electrons are emitted
per second but does not increase their energy.
16
The photoelectric effect, cont’d
 The energy of a single photon is miniscule.
 A convenient unit is the electron-Volt (eV).
1 electronvolt  1.6 10
19
1 eV  1.6 10
19

coulomb 1 volt
J
One electron-volt is the potential energy of
each electron in a 1-volt battery.
17
Example
Example 10.1
Compare the energies associated with a
quantum of each of the following types of EM
radiation.
14
f

4.3

10
Hz
red light:
14
f

6.3

10
Hz
blue light:
18
f

5

10
Hz
x ray:
18
Example
Example 10.1
ANSWER:
For red light:
E  hf

 4.136 10
15

eV/Hz 4.3 10 Hz
14

 1.78 eV
19
Example
Example 10.1
ANSWER:
For blue light:
E  hf

 4.136 10
15

eV/Hz 6.3 10 Hz
14

 2.61 eV
20
Example
Example 10.1
ANSWER:
For an x ray:
E  hf

 4.136 10
15

eV/Hz 5 10 Hz
18

 20, 700 eV
21
Example
Example 10.1
DISCUSSION:
Notice the significant increase in the energy of
the x ray compared to the visible light.
This explains why high doses of x rays can do
serious damage to living cells.
22
Applications of the photoelectric
effect
 The photoelectric effect is the key to
“interfacing” light with electricity.
 The figure shows a schematic of a device that
can detect light.
23
Applications of the photoelectric
effect, cont’d
 When light strikes the metal plate, electrons
are emitted.
 The electrons are pushed across the tube
because of the potential difference.
24
Applications of the photoelectric
effect, cont’d
 The flow of electrons “closes” the circuit.
 The ammeter then measures the current flow
due to the electrons.
 Since there is a current, there is light.
25
Applications of the photoelectric
effect, cont’d
 A similar approach works for photocopiers.
26
Atomic spectra
 The third problem that classical physics could
not resolve is the emission spectra of the
elements.
 Imagine shining the light from a heated
filament through a prism.
 The light is separated into a range of colors.
 This spectrum is called a continuous
spectrum since it is a continuous band of
colors.
27
Atomic spectra, cont’d
 Now imagine heating a gas-filled tube.
 The gas will emit some EM radiation.
 After this light passes through a prism, only
certain lines of color appear.
28
Atomic spectra, cont’d
 This type of spectrum is called an emission-
line spectrum.

Because it is due to the light emitted by the
gas and it is not continuous.
29
Atomic spectra, cont’d
 Here are some
emission spectra
for various
elements.
 Notice that each
has its own
distinct sets of
lines.
30
Bohr model of the atom
 Bohr constructed a model of the atom called
the Bohr model:

The atom forms a miniature “solar system.”


The electron orbits are quantized.


the nucleus is at the center and the electrons
move about the nucleus in well-defined orbits.
the electrons can only be in certain orbits about a
given atomic nucleus.
Electrons may “jump” from one orbit to
another.
31
Bohr model of the atom, cont’d
 Here is a figure that
illustrates the Bohr
model.


The electron orbits
the nucleus.
The electron can
only orbit in
specific orbits.
32
Bohr model of the atom, cont’d
 Transitions from one orbit to another involve
discrete amounts of energy.

The energy to change levels is the difference in the two
energy levels.
33
Bohr model of the atom, cont’d
 Let’s consider hydrogen.

One electron and one proton.
 Orbit 1 is the innermost orbit and corresponds
to the lowest energy state of the electron.
 The amount of energy required to just remove
an electron from the proton is the ionization
energy.


The electron is no longer bound to the nucleus.
The atom is ionized because there is no longer the
same number of electrons and protons.
34
Bohr model of the atom, cont’d
 Imagine an electron that is in the sixth
allowed orbit.

So it has energy E6.
 Let the electron make a transition to the
second orbit.

So it has energy E2.
 The electron must lose energy in the amount
E  E6  E2
35
Bohr model of the atom, cont’d
 This is called a radiative transition because
the electron loses energy by emitting a
photon of the appropriate energy.
 The change in energy of the electron must
equal the photon energy:
E  E6  E2  hf

This gives a formula for the frequency of the
emitted light according to which orbits are
involved in the transition.
36
Bohr model of the atom, cont’d
 The frequency of the emitted light is
proportional to the energy of the electron
orbits involved in the
transition.
 A downward electron
transition can also
occur during a collision
with another particle.

A collisional transition.
37
Bohr model of the atom, cont’d
 An atom can also absorb a photon.
 The electron can gain energy from the
incoming photon.
 This increase in the
electron’s energy
causes it to transition
to a higher energy
orbit.
38
Bohr model of the atom, cont’d
 If broad-spectrum light is passed through a
material, the light will cause transitions to
higher energy orbits.
 This reduces the number of photons of the
corresponding energy.
39
Bohr model of the atom, cont’d
 The spectrum emerging from the material has
dark bands at certain frequencies.
 This type of spectrum is called an absorption
spectrum.
40
Bohr model of the atom, cont’d
 One unexplained result of the Bohr model
was that the angular momentum of the
electron in its orbit is quantized.
 Mathematically, this means the allowed
angular momentum can only have the values:
h
h
h
, or 2
, or 3 , ...
2
2
2
41
Quantum mechanics
 Even with its shortcomings, the Bohr model
indicated that new physics was needed to
describe the atom.
 Louis de Broglie proposed that electrons
have wavelike properties.

We know that light has wave-like properties.


diffraction, refraction, etc.
We also know light has particle-like properties.

blackbody radiation, photoelectric effect, etc.
42
Quantum mechanics, cont’d
 He suggested that the wavelength of a
particle depends on its momentum.

Recall that momentum is the product of mass
and velocity.
h

mv
 So the higher the momentum, the shorter the
wavelength.

That means the higher the frequency.
43
Example
Example 10.2
What is the de Broglie wavelength of an
electron with speed 2.19×106 m/s? (This is
the approximate speed of an electron in the
smallest orbit in hydrogen.)
The electron mass is 9.11×10-31 kg.
44
Example
Example 10.2
ANSWER:
The problem gives us:
m  9.1110
31
kg
v  2.19 10 m/s
6
The de Broglie wavelength is then:
34
h
6.63 10 J-s


31
6
mv
9.1110 kg 2.19 10 m/s

 3.3 10

10

m  0.332 nm.
45
Example
Example 10.2
DISCUSSION:
This wavelength is on the same length scale as
the diameter of atoms.
Thus electrons are useful for probing the
structure of atoms.
46
Quantum mechanics, cont’d
 Experiments were performed by shooting
electrons and x-rays through a solid.
 The same diffraction pattern was obtained.
47
Quantum mechanics, cont’d
 de Broglie’s hypothesis was also able to
explain Bohr’s quantized orbits.
 Since the electron acts like a wave, the wave
must fit along the circumference of the
electron’s orbit.
 This means that only
orbits with wholenumbered multiples
of the wavelength
are valid.
48
Quantum mechanics, cont’d
 Since the circumference must equal some
multiple of the wavelength:
2 r   or 2 or ...
 This means
h
h
2 r   
 mrv 
mv
2

This supports the Bohr model.
49
Example
Example 10.3
Using the results of Example 10.2, find the
radius of the smallest orbit in the hydrogen
atom.
  0.332 nm
50
Example
Example 10.3
ANSWER:
The radius is:
 0.332 nm
r

2
2  3.14
 0.0529 nm.
51
Quantum mechanics, cont’d
 These developments introduce an entirely
new branch of physics called quantum
mechanics.

It deals with physical systems that are
quantized.
 A pivotal contribution is called the
Heisenberg uncertainty principle.
 It is based on the observation that atoms are
actually composed of objects that have wavelike properties.
52
Quantum mechanics, cont’d
 The difference between a wave and a particle
is physical extent.


We can imagine a particle as a small ball with
a precise position.
A wave must be spread out and does not have
a precise position.
 So our particles are more like fuzzy cotton
balls rather than shrunken marbles.
 This means you cannot precisely state their
position.
53
Quantum mechanics, cont’d
 Heisenberg was able to develop the formula:
x mv  h



x is the uncertainty of the particle’s position,
mv is the uncertainty of the particle’s
momentum, and
h is Planck’s constant.
 This means if you have high certainty of
where the particle is, you have little
knowledge of what its momentum is.
 So the resolution of our experiments is limited
by nature — not because of our ignorance.
54
Quantum mechanics, cont’d
 Schrödinger established a model in which the
hydrogen atom is described by a wave
function.
 The wave function describes the probability of
finding the atom in a particular configuration.
55
Atomic structure
 We now know that the Bohr model is not
accurate.
 The atom is actually
pictured as a tiny
nucleus surrounded
by an “electron
cloud.”

The density of the cloud
indicates the probability
of the finding the
electron at some point.
56
Atomic structure, cont’d
 Since the exact position of the electron is not
known, it is more useful to describe the
electron’s orbit by its energy.
 The electrons are described as being in
certain allowed energy states called energy
levels.
 The lowest energy level is called the ground
state.
 The higher energy states are referred to as
excited states.
57
Atomic structure, cont’d
 These energy states are represented by an
energy-level diagram.
 Each energy level
is labeled with a
quantum number,
n.

The ground state
has n = 1.
58
Atomic structure, cont’d
 The difference in energy between adjacent
states decreases as n increases.
 The highest state
is labeled as n = .

This energy is the
ionization energy.
 The numbers on the
left of the energy-level
diagram indicate the
energy of each state.
59
Atomic structure, cont’d
 The negative values indicate that the electron
is bound to the nucleus.
 The change in
electron energy as
a result of an
“energy-level
transition” is found
by comparing the
energies of the
two states.
60
Atomic structure, cont’d
 The photon energy for a transition between
the ground state (n = 1) and the first excited
state (n = 2) is:
E  E2  E1
 3.4 eV   13.6 eV 
 10.2 eV.

Referring to Figure 10.7,
this is a photon of UV
light.
 The frequency is
2.5×1015 Hz.
61
Atomic structure, cont’d
 Here is a diagram of several downward
transitions.
 For each
transition,
the
wavelength
is given in
nanometers.
62
Atomic structure, cont’d
 From this figure, some conclusions may be
inferred.



Transitions to the ground state (n = 1) result in the
emission of ultraviolet photons.
 This series of emission lines is referred to as the Lyman
series.
Transitions from higher energy levels to the first excited
state (n = 2) result in the emission of visible photons.
 This series is referred to as the Balmer series.
Transitions from higher levels to n = 3 result in the
emission of infrared photons.
 This series is referred to as the Paschen series.
63
Example
Example 10.4
Find the frequency and wavelength of the
photon emitted when a hydrogen atom goes
from the n = 3
state to the
n = 2 state.
64
Example
Example 10.4
ANSWER:
From the figure, we find:
E2  3.4 eV
E3  1.51 eV
So the energy is:
E  E3  E2
 1.51 eV   3.4 eV 
 1.89 eV.
65
Example
Example 10.4
ANSWER:
The frequency is:
E
1.89 eV
f  
15
h 4.136 10 eV/Hz
 4.57 10 Hz.
14
66
Example
Example 10.4
ANSWER:
Which gives a wavelength of:
c
3 10 m/s
 
14
f 4.57 10 Hz
8
7
 6.57 10 m  657 nm.
67
Example
Example 10.4
DISCUSSION:
This wavelength corresponds to a photon of
visible light — red.
68
Atomic structure, cont’d
 An electron does not have to make a direct
“jump” to a certain energy level.
 For an electron in the
n = 4 level, it can
transition to n = 2 and
then to the n = 1 level.
 Such a process is
called a cascade.
69
Atomic structure, cont’d
 The energy-level diagram helps illustrate
what happens when hydrogen gas in a tube
is heated to high temperatures or excited by
passing an electric current through it.




The atoms will be excited into higher energy levels.
The excited atoms will undergo transitions to lower
energies, emitting photons.
Although several transitions are possible for a given
temperature, some are more favored.
Such a system produces the emission spectrum of
hydrogen.
70
Atomic structure, cont’d
 Here are two examples of emission spectra
for excited gases.

A neon sign and the aurora borealis.
71
Atomic structure, cont’d
 So far, we’ve only discussed hydrogen.

It is the simplest element since it only has a single
electron.
 As you examine elements of higher atomic number,
the number of electrons increases.

For the neutral atom, the atomic number indicates
the number of electrons.
 By examining the emission spectra of various
elements, Wolfgang Pauli discovered that certain
transitions to lower states did not occur when the
lower states were already occupied.
72
Atomic structure, cont’d
 This led him to develop the Pauli exclusion
principle:

Two electrons cannot occupy precisely the same
quantum state at the same time.
 This applies to an entire class of elementary
particles, known as fermions.
 The electron is just one species of this class.
 For each energy level, there exist a set number
of quantum states available to the electron.
73
Atomic structure, cont’d
 Once all the quantum states are occupied for
a given energy level, additional electrons
must occupy other energy levels that have
vacancies.
 The number of electrons available for each
energy level are:




n = 1 can have no more than 2 electrons.
n = 2 can have no more than 8 electrons.
n = 3 can have no more than 18 electrons.
The general rule is 2n2 electrons for energy level n.
74
Atomic structure, cont’d
 Here are some examples.
75
Atomic structure, cont’d
 The structure of the periodic table of
elements reflects the idea behind the Pauli
exclusion principle.
76
Laser
 The word laser is an acronym derived from
the phrase “Light Amplification by Stimulated
Emission of Radiation.”
 Imagine an electron in an atom has been
excited to some higher energy level.

This might be due to a collision or by
absorption of a photon.
 The electron will remain in this state for only a
short time.
77
Laser, cont’d
 If this decay to a lower energy level occurs
spontaneously, a photon will be emitted in
some random direction.
 There is an alternative process through which
the electron can return to its original energy
level:
stimulated
emission.
78
Laser, cont’d
 This involves a second photon of the same
energy as the original photon.
 Consider a group of atoms, having their
electrons in this same excited state, that is
“bathed” in light consisting of photons with
energy E.
 The atoms will be stimulated to decay by
emitting additional photons of energy E.
 This increases the intensity of the light.
79
Laser, cont’d
 The stimulating radiation
and the additional emitted
radiation are in phase.

The crests and troughs of
the EM waves at a given
point all match up.
 Such radiation is said to be
coherent.

Ordinary light is incoherent.
80
Laser, cont’d
 To achieve this light amplification requires
some ingenuity.
 Most excited states decay very quickly.
 Some states are called metastable because
they do not decay for a much longer time.

Perhaps 0.000 1 s instead of 0.000 000 000 1 s.
 Atoms in this state do not decay during the
time it takes to excite more than half of the
other atoms.

This process is called pumping.
81
Laser, cont’d
 With such a majority of atoms in the upper
energy level, such a situation is called
population inversion.
 Here is an energy-level diagram indicating
the population inversion.
82
Laser, cont’d
 Here is a schematic of a ruby laser system.
83