* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Exam 2 Equation Sheet
Quadratic equation wikipedia , lookup
Cubic function wikipedia , lookup
Elementary algebra wikipedia , lookup
Quartic function wikipedia , lookup
System of polynomial equations wikipedia , lookup
Corecursion wikipedia , lookup
History of algebra wikipedia , lookup
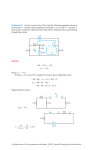
Exam 2 Equation Sheet Capacitor dv C dt = q Cv Inductor di = vL L L dt = W = iC C = W 1 2 Li2 1 2 2 Cv = q2 = 2C 1 2 = iL (t) iL (t o ) + qv v C= (t) v(t o ) + 1 idt C∫ 1 vdt L∫ First Order Circuits Natural Response RC-Circuit: v C (t) = VOC + [v c (0 − ) − VOC ]e − t / τ where= τ R ThCeq and VOC = v Th RL-Circuit: τ L eq / R Th and ISC = iL (t)= ISC + [iL (0 − ) − ISC ]e − t / τ where = iN Forced Response Step 1: Use KVL or KCL to derive the differential equation dx/dt + ax(t) = f(t) Step 2: The general solution is of the form x(t) = x f (t) + xn (t) where x n (t) = Ae-t/τ Step 3: Assume the forcing response to be the form -at when v s (t), is (t) = Ke-at B e x f (t) = 1 (t) K sin( ωt) B1 sin(ωt) + B2 cos(ωt) when v s (t), is= Step 4: Substitute assumed solution into Step 1 to find constants B 1 and B 2 . Step 5: Apply initial conditions [v C (0−) or i L (0−)] to the general solution to obtain the constant A. Step 6: Solve the circuit problem and interpret Second Order Circuits Step 1: Use KVL, KCL, v L = Ldi L /dt, and i C = Cdv C /dt to obtain two first order response equation. Be sure that these equations dependent on v C and i L . Step 2: Set all sources equal to zero to obtain the Natural Response (x n (t)) and solve the characteristic equation for the roots. s2 + 2αs + ω02 = 0 ⇒ s1,s2 = −α ± α 2 − ω02 Step 3: The natural response of the circuit depends only on the values of R, L, and C which dictates the types of roots s 1 and s 2 . The 3 possible solutions are • Critical Damping ― α = ω0 : x critical (t) = e −αt (A1t + A 2 ) • Overdamping ― α > ω0 : x over = (t) A1es1t + A 2 es2 t • Underdamping – α < ω0 : xunder (t) = e−αt (A1 cos ωd t + A 2 sin ωd t), where ωd = Step 4: The forcing response x f (t) has the same form as the effective source: ω02 − α 2 Forcing Function K = constant Ke− at K sinat or K cosat Assumed Solution x f (t) = B x f (t) = Be− at = x f (t) B1 cosat + B2 sinat Find the constant B and write out the complete response. Step 5: Find the initial conditions x 2 (0−) and dx 2 (0−)/dt. This is a two-step process; • Find the steady-state values for the capacitor’s voltage v C (0−) and the inductor’s current i L (0−) before the switch is thrown. • To find the derivative dx 2 (0+)/dt after the switch has been thrown, use equation 2 in Step 1 and solve for it numerically. Step 6: Apply the initial conditions of Step 5 to find the constants A 1 and A 2 . • Setup up two equations involving x 2 (0+) and dx 2 (0+)/dt and solve for A 1 and A 2 • Write down the Total Response for the circuit: x(t) = x n (t) + x f (t) Step 7: Solve the circuit problem and interpret