* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 2(3x+7y=188)
Debye–Hückel equation wikipedia , lookup
Maxwell's equations wikipedia , lookup
Two-body problem in general relativity wikipedia , lookup
BKL singularity wikipedia , lookup
Itô diffusion wikipedia , lookup
Perturbation theory wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Equation of state wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Unification (computer science) wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Calculus of variations wikipedia , lookup
Equations of motion wikipedia , lookup
Differential equation wikipedia , lookup
Schwarzschild geodesics wikipedia , lookup
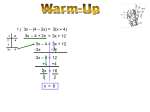
The Problem Stephanie is trying to buy oboe reeds. She can play using either a medium reed, or medium-hard reed. At the online store, Reedbay, she can get 4 medium reeds and 2 medium-hard reeds for $109.50. On the other hand, she could get 3 medium reeds and 7 medium-hard reeds for $188.00. How much does each reed type cost? Substitution Substitution tends to be tricky and complicated. It has several steps, making errors almost inevitable. Choosing the wrong variable or problem can make substitution difficult and confusing, proving that elimination is the better method. 4x+2y=109.5 3x+7y=188 First, you have to choose one of the two equations and isolate a variable. In this case, x is used. 4x+2y=109.5 -2y -2y 4x=109.5-2y /4 /4 x=109.5-2y 4 3(109.5-2y)+7y=188 4 82.1-1.5y+7y=188 82.1+5.5y=188 -82.1 -82.1 5.5y=105.9 /5.5 /5.5 y=19.25 Next you plug the resulting solution into the other equation and solve for the other variable, y. 4x+2(19.25)=109.5 4x+38.5=109.5 -38.5 -38.5 4x=71 /4 /4 x=17.75 (17.75, 19.25) You then have to plug in the solution you got for the latter variable, y, into the first equation and solve the equation for the original variable, x. Elimination As you can see, elimination is clearly the better method. It has a simple concept and has fewer steps than substitution and graphing. This can help prevent any mistakes that might be made. The first step is to combine the two equations. To do this you multiply the whole problems, so that when they’re 4x+2y=109.5 added together at least one variable will be 3x+7y=188 canceled. From there, you simplify the resulting equation until you find a solution 7(4x+2y=109.5) -2(3x+7y=188) for the remaining variable, x. 28x+14y=766.5 -6x+(-14y)=-376 22x=390.5 /22 /22 x=17.75 Then you plug the variable’s solution into one of the problems and solve for the other variable, y. 3(17.75)+7y=188 53.25+7y=188 -53.25 -53.25 7y=134.75 /7 /7 y=19.25 (17.75, 19.25) Graphing Prices can be particularly hard to deal with when using graphing because they don’t always divide evenly. Unlike elimination, graphing requires the two equations to be in slope intercept form, or, y=mx+b. 4x+2y=109.5 3x+7y=188 4x+2y=109.5 -4x -4x 2y=-4x+109.5 /2 /2 y=-2x+54.75 3x+7y=188 -3x -3x 7y=-3x+188 /7 /7 y=-3/7x+188/7 Elimination...in Oboe & in all Oboe-Related Activities… Inc. is a corporation that deals with math in oboe related situations. This includes reeds, cases, cleaning cloths, cork grease, actual oboes, sheet music, and, among other things, oboe ninjas. They’re everywhere. And if you don’t use elimination, they WILL be angered. Depression hurts. Not using elimination could hurt even more. Elimination…In Oboe & in all Oboe-Related Activities…Inc. But what if you had a different problem? What if your equations were:7x + 2y = 16 Elimination –21x – 6y = 24 3(7x + 2y = 16) –21x – 6y = 24 21x+6y=48 -21x-6y=24 0=72 This equation has no solution. The lines would be parallel. Substitution 7x + 2y = 16 –21x – 6y = 24 7x+2y=16 -7x -7x 2y=-7x+16 /2 /2 y=-(7/2)x+8 -21x-6(-(7/2)x+8)=24 -21x+21x-48=24 -48=24 This nonsense answer means that, again, there is no solution and that the lines would be parallel. Graphing 7x + 2y = 16 –21x – 6y = 24 7x+2y=16 -7x -7x 2y=-7x+16 /2 /2 y=-3.5x+8 -21x-6y=24 +21x +21x -6y=21x+24 /-6 /-6 y=-3.5x-3 As you can see, the lines are parallel. This means that the equation has no solution. Or maybe the equations are: 12x+5y=24 Elimination 24x+10y=48 -2(12x+5y=24) 24x+10y=48 -24x-10y=-48 24x+10y=48 0=0 This equation has infinitely many solutions. Both equations represent the same line. This can be written as (x,y) 12x+5y=24. Graphing 12x+5y=24 24x+10y=48 12x+5y=24 -12x -12x 5y=-12x+24 /5 /5 y=-2.4x+4.8 24x+10y=48 -24x -24x 10y=-24x+48 /10 /10 y=-2.4+4.8 As you can see, these equations represent the same line. Therefore there are infinitely many solutions. Substitution 12x+5y=24 24x+10y=48 12x+5y=24 -5y -5y 12x=24-5y /12 /12 x=2-(5/12)y 24(2-(5/12)y)+10y=48 48-10y+10y=48 48=48 -48 -48 0=0 This equation has infinitely many solutions, meaning that they each represent the same line. In conclusion… Elimination is the best method for working these problems. It has a simple concept and uses a minimal amount of work. Since there are fewer steps than substitution and graphing, there is not quite as much room for error.