Download Logic3

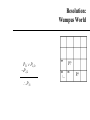
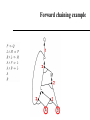
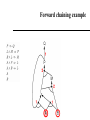
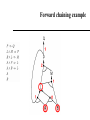
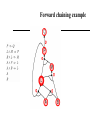
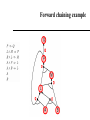
CS 4700:
Foundations of Artificial Intelligence
Carla P. Gomes
[email protected]
Module:
Propositional Logic:
Inference
(Reading R&N: Chapter 7)
1
Proof Methods
2
Proof methods
Proof methods divide into (roughly) two kinds:
– Application of inference rules
• Legitimate (sound) generation of new sentences from old
• Proof = a sequence of inference rule applications
Can use inference rules as operators in a standard search algorithm
• Different types of proofs
– Model checking
• truth table enumeration (always exponential in n)
Current
module
we’ve talked about this approach
• improved backtracking, e.g., Davis--Putnam-Logemann-Loveland
(DPLL)
• (including some inference rules)
• heuristic search in model space (sound but incomplete)
e.g., min-conflicts-like hill-climbing algorithms
Next
module
Proof
The sequence of wffs (w1, w2, …, wn) is called a proof (or deduction) of wn from
a set of wffs Δ iff each wi in the sequence is either in Δ or can be inferred from a
wff (or wffs) earlier in the sequence by using a valid rule of inference.
If there is a proof of wn from Δ, we say that wn is a theorem of the set Δ.
Δ├ wn
(read: wn can be proved or inferred from Δ)
The concept of proof is relative to a particular set of inference rules used. If we
denote the set of inference rules used by R, we can write the fact that wn can be
derived from Δ using the set of inference rules in R:
Δ├ R wn
(read: wn can be proved from Δ using the inference rules in R)
Propositional logic:
Rules of Inference or Methods of Proof
How to produce additional wffs (sentences) from other ones? What steps can we
perform to show that a conclusion follows logically from a set of hypotheses?
Example
Modus Ponens
P
PQ
______________
Q
The hypotheses (premises) are written in a column and the conclusions below the bar
The symbol  denotes “therefore”. Given the hypotheses, the conclusion follows.
The basis for this rule of inference is the tautology (P  (P  Q))  Q)
[aside: check tautology with truth table to make sure]
In words: when P and P  Q are True, then Q must be True also. (meaning of
second implication)
6
Propositional logic:
Rules of Inference or Methods of Proof
Example
Modus Ponens
If you study the CS 4700 material  You will pass
You study the CS4700material
______________
 you will pass
Nothing “deep”, but again remember the formal reason is that
((P ^ (P  Q))  Q is a tautology.
7
Propositional logic:
Rules of Inference or Method of Proof
Rule of Inference
Tautology (Deduction Theorem)
Name
P
PQ
P  (P  Q)
Addition
PQ
P
(P  Q)  P
Simplification
P
Q
PQ
[(P)  (Q)]  (P  Q)
Conjunction
P
PQ
Q
[(P)  (P Q)]  (P  Q)
Modus Ponens
Q
PQ
 P
[(Q)  (P Q)]  P
Modus Tollens
PQ
QR
 P R
[(PQ)  (Q  R)]  (PR)
Hypothetical Syllogism
(“chaining”)
PQ
P
Q
[(P  Q)  (P)]  Q
Disjunctive syllogism
PQ
P  R
QR
[(P  Q)  (P  R)]  (Q  R)
Resolution
Valid Arguments
An argument is a sequence of propositions. The final proposition is called the
conclusion of the argument while the other propositions are called the
premises or hypotheses of the argument.
An argument is valid whenever the truth of all its premises implies the truth of
its conclusion.
How to show that q logically follows from the hypotheses (p1  p2  …pn)?
Show that
(p1  p2  …pn)  q is a tautology
One can use the rules of inference to show the validity of an argument.
9
Proof Tree
Proofs can also be based on partial orders – we can represent them using a
tree structure:
– Each node in the proof tree is labeled by a wff, corresponding to a wff in
the original set of hypotheses or be inferable from its parents in the tree
using one of the rules of inference;
– The labeled tree is a proof of the label of the root node.
Example:
Given the set of wffs:
P, R, PQ
Give a proof of Q  R
10
Tree Proof
Given: P, P Q, R;
Prove: Q  R
P
PQ
R
MP
Q
Conj.
QR
What rules of inference
did we use?
11
Length of Proofs
Why bother with inference rules? We could always use a truth table
to check the validity of a conclusion from a set of premises.
But, resulting proof can be much shorter than truth table method.
Consider premises:
p_1, p_1  p_2, p_2  p_3 … p_(n-1)  p_n
To prove conclusion: p_n
Inference rules: n-1 P steps
Truth table:
2n
Key open question: Is there always a short proof for any valid
conclusion? Probably not. The NP vs. co-NP question.
Resolution in Propositional Logic
Resolution
(for CNF)
Very important inference rule – several other inference rules
can be seen as special cases of resolution.
PQ
P  R
 QR
Soundness of rule (validity of rule):
[(P  Q)  (P  R)]  (Q  R) is valid
Resolution for CNF – applied to a special type of wffs: conjunction of clauses.
Literal – either an atom (e.g., P) or its negation (P).
Clause – disjunction of of literals (e.g., (P  Q  R)).
Note: Sometimes we use the notation of a set for a clause: e.g. {P,Q,R} corresponds
to the clause (PQ R); the empty clause (sometimes written as Nil or {}) is equivalent
to False;
Soundness of Resolution:
Validity of the Resolution Inference Rule
PQ
P  R
 QR
resolving on P
Validity (Tautology): (P  Q) (P  R)
P
Q
R
(PQ)
(PR)
(PQ)(PR)
(QR)
(P  Q) (P  R)  (Q  R)
0
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
1
1
1
1
1
1
0
0
1
0
0
0
1
1
1
0
1
0
0
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
1
0
0
0
0
1
0
0
1

(Q  R)
;
Resolution:
Special Cases
1 – Rule of Inference: Chaining
RP
P  Q
 RQ
R  P
PQ
 R Q
can be re-written
Rule of Inference Chaining
2 – Rule of Inference: Modus Ponens
P
P  Q
 Q
can be re-written
P
PQ
 Q
Rule of Inference: Modus Ponens
Resolution:
Special Cases
3 – Unit Resolution
P
P Q
 Q
P
P  Q
 Q
Resolution:
Caution!
No duplications in the resolvent set
only one instance of Q
appears in the resolvent,
which is a set!
PQRS
P  Q  W
 QRSW
DO NOT Resolve
on Q and R
Resolving one pair at a time
Resolving
on Q

P  Q  R
P  W  Q  R
P  R  R  W
P  Q  R
P  W  Q  R
 P  Q  Q  W
Resolving
on R
True

P  Q  R
P  W  Q  R
PW
CNF
Conjunctive Normal Form (CNF)
A wff is in CNF format when it is a conjunction of disjunctions of literals.
(P  Q  R) (S  P  T R) (Q  S)
Resolution for CNF – applied to wffs in CNF format.
Resolution
{λ}  Σ1
{ λ}  Σ2
 Σ1  Σ2
Resolvent of the
two clauses
Σi- sets of literals
i =1 ,2
λ – atom;
atom resolved upon
Conversion to CNF
P  (Q  R)
1.Eliminate , replacing α  β with (α  β)(β  α).
(P  (Q  R))  ((Q R)  P)
2. Eliminate , replacing α  β with α β.
(P  Q  R)  ((Q R)  P)
3. Move  inwards using de Morgan's rules and doublenegation:
(P Q R)  ((Q R)  P)
4. Apply distributivity law ( over ) and flatten:
(P  Q  R)  (Q P)  (R  P)
Converting DNF (Disjunctions of
conjunctions) into CNF
1 – create a table – each row
corresponds to the literals in each
conjunct;
2 - Select a literal in each row and
make a disjunction of these literals;
Example:
(PQ R ) (S R P) (Q S  P)
P
Q
R
S
R
P
Q
S
P
(P  S  Q)  (P  R  Q) (P  P  Q) (P  S  S)
(P  R  S) (P  P  S) (P  P  Q)…
How many clauses?
Resolution:
Wumpus World
P31  P2,2,
P2,2
 P31
P?
P?
Resolution Refutation
Resolution is sound – but resolution is not complete – e.g., (P R) ╞ (P  R) but
we cannot infer (P  R) using resolution 
we cannot use resolution directly to decide all logical entailments.
!
Resolution is Refutation Complete:
We can show that a particular wff W is entailed from a given KB, how?
!
Proof by contradiction:
Write the negation of what we are trying to prove (W) as a conjunction of clauses;
Add those clauses (W) to the KB (also a set of clauses), obtaining KB’; prove
inconsistency for KB’, i.e.,
Apply resolution to the KB’ until:
•
•
No more resolvents can be added
Empty clause is obtained
To show that (P  R) ╞Res (P  R) do: (1) negate (P  R), i.e.: (P) (R) ; (2) prove that
(P  R)  (P) (R) is inconsistent
Propositional Logic:
Proof by refutation or contradiction:
Satisfiability is connected to inference via the
following:
KB ╞ α if and only if (KB α) is unsatisfiable
One assumes α and shows that this leads to a
contradiction with the facts in KB
Resolution:
Robot Domain
Example:
BatIsOk
RobotMoves
BatIsOk  BlockLiftable RobotMoves
Show that KB ╞ BlockLiftable
KB
BatIsOk  BlockLiftable  RobotMoves
BlockLiftable
BatIsOk
RobotMoves
BatIsOk  BlockLiftable  RobotMoves
BlockLiftable
KB’
RobotMoves
BatIsOk  RobotMoves
BatIsOk
Nil
BatIsOk
Resolution
Resolution is refutation complete (Completeness of resolution refutation):
If KB ╞ W, the resolution refutation procedure, i.e., applying
resolution on KB’, will produce the empty clause.
Decidability of propositional calculus by resolution refutation:
If KB is a set of finite clauses and if KB ╞ W, then the resolution
refutation procedure will terminate without producing the empty
clause.
Ground Resolution Theorem
– If a set of clauses is not satisfiable, then resolution closure of those
clauses contains the empty clause.
In general, resolution for propositional logic
is exponential !
The resolution closure of a set of clauses W in CNF, RC(W), is the set of all clauses derivable by repeated application
of the resolution rule to clauses in W or their derivatives.
Resolution example:
Wumpus World
KB = (B1,1  (P1,2 P2,1))  B1,1
α = P1,2
Resolution example:
Wumpus World
KB = (B1,1  (P1,2 P2,1))  B1,1
α = P1,2
KB = (B11  (P1,2 P2,1)) ^ ((P1,2 P2,1)  B11)  B1,1
=(B11  P1,2 P2,1) ^ ((P1,2 P2,1)  B11)  B1,1
=(B11  P1,2 P2,1) ^(( P1,2 ^  P2,1)  B11))  B1,1
=(B11  P1,2 P2,1) ^( P1,2  B11) ^ ( P2,1  B11)  B1,1
Resolution example:
Wumpus World
KB = (B1,1  (P1,2 P2,1))  B1,1
α = P1,2
KB = (B11  (P1,2 P2,1)) ^ ((P1,2 P2,1)  B11)  B1,1
=(B11  P1,2 P2,1) ^ ((P1,2 P2,1)  B11)  B1,1
=(B11  P1,2 P2,1) ^(( P1,2 ^  P2,1)  B11))  B1,1
=(B11  P1,2 P2,1) ^( P1,2  B11) ^ ( P2,1  B11)  B1,1
Resolution algorithm
Proof by contradiction, i.e., show KBα unsatisfiable
New resolvents added at the end
Resolution algorithm
Proof by contradiction, i.e., show KBα unsatisfiable
New resolvents added at the end
Any complete search algorithm applying only the resolution rule, can derive any
conclusion entailed by any knowledge base in propositional logic – resolution can
always be used to either confirm or refute a sentence – refutation completeness (Given
A, it’s true we cannot use resolution to derive A OR B; but
we can use resolution to answer the question of whether A OR B is true.)
Resolution Closure
Definition
The resolution closure RC(f) of a formula f in CNF is the set of
all clauses derivable by repeated application of the resolution rule
to clauses in f or their derivatives.
Resolution
Theorem (Ground Resolution Theorem)
– If f ( in CNF) is unsatisfiable then RC(f) contains the empty clause (that
evolves from P¬P for some variable P).
Proof (by contraposition)
If RC(f) does not contain the empty clause then it is satisfiable.
Let the variables in f be P1,..,Pn, and let us assume that RC(f) does not contain
the empty clause.
Therefore we can construct a model for m for f with suitable truth
values for P1,..,Pn.
Resolution (contd.)
Construction procedure:
For i=1,..,n, if there exists a clause in RC(f) containing the
literal ¬Pi such that all its other literals are false under
the assignment chosen for P1,..,Pi-1, then assign false
to Pi. . Otherwise we set Pi=True.
Claim: RC(f)|m is true. I.e., m is a model for f.
Resolution (contd.)
Claim, RC(f)|m is true. I.e., m is a model for f.
Assume the opposite. Then, there exists a clause that evaluates to false
under m.
Consider a non-satisfied clause in RC(f) over variables P1,..Pi that
minimizes i.
Wlog, we may write this clause as (ab), where b is a literal over Pi and
a is a formula over variables P1,.., Pi-1.
Note that there cannot exist another such clause where b is negated
(c¬b) as otherwise i was not minimal [consider (ac)  RC(f)].
Resolution (contd.)
So we write the clause as (ab), with b a literal over Pi
However, then Pi is set such that b evaluates to True, which contradicts the
assumption that the clause was not satisfied.
Therefore all the clauses are satisfied and m is indeed a model for RC(f).
QED
Resolution Refutation –
Ordering Search Strategies
Original clauses – 0th level resolvents
– Breadth first strategy 
• Generate all 1st level resolvents, then
all 2nd level resolvents, etc.
– Depth first strategy 
• Produce a 1st level resolvent;
• Resolve the 1st level resolvent with a
0th level resolvent to produce a 2nd
level resolvent, etc.
• With a depth bound, we can use a
backtrack search strategy;
0th level resolvents
BatIsOk
RobotMoves
BatIsOk  BlockLiftable  RobotMoves
BlockLiftable
BatIsOk  BlockLiftable  RobotMoves
BlockLiftable
RobotMoves
BatIsOk  RobotMoves
BatIsOk
BatIsOk
Nil
Depth first strategy
Refinement Resolution Strategies
Set-of-support Resolution Strategy
Definitions:
A clause γ2 is a descendant of a clause γ1 iif:
–
–
Is a resolvent of γ1 with some other clause
Or is a resolvent of a descendant of γ1 with some
other clause;
BatIsOk  BlockLiftable  RobotMoves
BlockLiftable
If γ2 is a descendant of γ1, γ1 is an ancestor of γ2;
Set-of-support – set of clauses that are either clauses
coming from the negation of the theorem to be
proved or descendants of those clauses.
Set-of-support Strategy – it allows only refutations
in which one of the clauses being resolved is in
the set of support.
Set-of-support Strategy is refutation complete.
RobotMoves
BatIsOk  RobotMoves
BatIsOk
BatIsOk
Nil
Set-of-support Strategy
Refinement Strategies
Ancestry-filtered strategy – allows only resolutions in which at least one
member of the clauses being resolved either is a member of the
original set of clauses or is an ancestor of the other clause being
resolved;
The ancestry-filtered strategy is refutation complete.
Refinement Strategies
Linear Input Resolution Strategy – at least one of the clauses being
resolved is a member of the original set of clauses (including the
theorem being proved).
Linear Input Resolution Strategy is not refutation complete.
Example:
(P Q)
(P Q)
(P Q) (P Q) (P  Q) (P  Q)
Q
Q
This set of clauses is inconsistent; but there is
no linear-input
refutation strategy; but there is a resolution
refutation strategy;
(P  Q) (P  Q)
Nil
This is NOT
Linear Input
Resolution Strategy
:
Resolution and Pigeon Hole Principle
Consider a formula to represent the Pigeon Hole principle: (n+1) pigeons
in n holes.
Pij – pigeon i goes in hole j Pij  {0,1} i= 1, 2, …, n+1; j = 1, 2, …n
Each pigeon has to go in a hole:
Starting with pigeon 1
P11  P12  …  P1n
…
Pn+1,1  Pn+1,2  …  Pn+1,n
Resolution Proofs of PH
And?
Two pigeons cannot go in the same hole
P11  ~P21; P11  ~P31; … P11  ~Pn+1,1;
~P11  ~P21; ~P11  ~P31; … ~P11 ~Pn+1,1;
….
~Pn+1,n  ~P2,n; ~Pn+1,n  ~P3n; … ~Pn+1,n ~Pn,n;
Resolution proofs of PH take exponentially many steps:
Resolution proofs of inconsistency of PH require an exponential number of
clauses, no matter in what order we resolve the clauses (Armin Haken 85).
Related to NP vs. Co-NP questions
Horn Clauses
Horn Clauses
Definition:
A Horn clause is a clause that has at most one positive literal.
Examples:
P; P  Q;  P  Q;  P  Q  R;
Types of Horn Clauses:
Fact – single atom – e.g., P;
Rule – implication, whose antecendent is a conjunction
of positive literals and whose consequent consists of a single
positive literal – e.g., PQ  R; Head is R; Tail is (PQ )
Set of negative literals - in implication form, the antecedent is
a conjunction of positive literals and the consequent is empty.
e.g., PQ  ; equivalent to  P  Q.
Inference with propositional Horn clauses can be done in linear time !
P
P Q
 Q
Unit Resolution for Horn Clauses
P
P  Q
 Q
Theorem
– Unit resolution is refutation complete for HF, i.e. if kb¬a is a HF then
unit propagation shows that kb¬a is unsatisfiable iff kb╞ a.
Proof
– If kb¬a is not satisfiable then kb¬a must contain a clause that contains
one non-negated variable only:This clause must be a unit clause.
(otherwise consider the model that sets all variables to false).
– Using unit resolution of this variable with all other clauses essentially
eliminates the variable from the formula while preserving the Horn
property.
– Continuing this process, unit propagation hits P¬P iff the formula is not
satisfiable.
Forward chaining
HORN (Expert Systems and Logic Programming)
Horn Form (restricted)
KB = conjunction of Horn clauses
– Horn clause =
• proposition symbol; or
• (conjunction of symbols)  symbol
– E.g., C  (B  A)  (C  D  B)
–
Modus Ponens (for Horn Form): complete for Horn KBs
α1, … ,αn,
α1  …  αn  β
Deciding entailment with Horn clauses
can be done in linear time,
β
in the size of the KB
!
Forward Chaining:
Diagnosis systems
Example: diagnostic system
IF the engine is getting gas and the engine turns over
THEN the problem is spark plugs
IF the engine does not turn over and the lights do not come on
THEN the problem is battery or cables
IF the engine does not turn over and the lights come on
THEN the problem is starter motor
IF there is gas in the fuel tank and there is gas in the
carburator
THEN the engine is getting gas
Forward chaining
(Data driven reasoning)
Idea: fire any rule whose premises are satisfied in the KB,
– add its conclusion to the KB, until query is found
AND-OR graph
Forward
Chaining
Algorithm
Forward chaining is
sound and complete
for Horn KB
Count
P => Q
L and M => P
B and L => M
A and P => L
A and B => L
Agenda
Inferred
1
2
2
2
2
P
L
M
B
A
F
F
F
F
F
A
B
Forward chaining example
Forward chaining example
Forward chaining example
Forward chaining example
Forward chaining example
Forward chaining example
Forward chaining example
Forward chaining example
Forward
Chaining
Algorithm
Forward chaining is
sound and complete
for Horn KB
Count
P => Q
L and M => P
B and L => M
A and P => L
A and B => L
Agenda
Inferred
1
2
2
2
2
P
L
M
B
A
F
F
F
F
F
A
B
Backward chaining
Idea: work backwards from the query q:
to prove q by BC,
check if q is known already, or
prove by BC all premises of some rule concluding q
Avoid loops: check if new subgoal is already on the goal stack
Avoid repeated work: check if new subgoal
1. has already been proved true, or
2. has already failed
Forward vs. backward chaining
FC is data-driven, automatic, unconscious processing,
– e.g., object recognition, routine decisions
May do lots of work that is irrelevant to the goal
BC is goal-driven, appropriate for problem-solving,
– e.g., Where are my keys? How do I get into a PhD program?
Complexity of BC can be much less than linear in size of KB in pactice.
Prominent expert systems
• CADUCEUS (expert system)- Blood-borne infectious bacteria
• Dendral- Analysis of mass spectra
• Jess- Java Expert System Shell. A CLIPS engine implemented in Java
used in the development of expert systems
• LogicNets- Web based expert system modeling environment to create
expert systems (in collaboration with NASA)
• Mycin - Diagnose infectious blood diseases and recommend antibiotics
(by Stanford University)
• NEXPERT Object- An early general-purpose commercial backwardschaining inference engine used in the development of expert systems
• Prolog- Programming language used in the development of expert
systems
• R1 (expert system)/XCon Order processing
• STD Wizard - Expert system for recommending medical screening tests
• PyKe- Pyke is a knowledge-based inference engine (expert system)