* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Circle - geometry
Duality (projective geometry) wikipedia , lookup
Line (geometry) wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Perceived visual angle wikipedia , lookup
Lie sphere geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
Problem of Apollonius wikipedia , lookup
History of trigonometry wikipedia , lookup
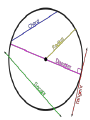
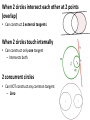
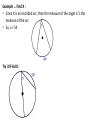
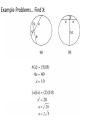
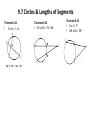
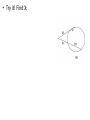
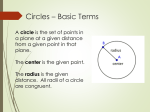
Chapter 9 Kiara, Chelsea, Angus 9.1 Basic Terms of the Circle Circle • Set of points in a plane at a given distance (radius) from a given point (center) • Nothing in interior is considered a circle • 2D Sphere • Set of points in space w/ distance (radius) from a given point • 3D Tangent • A line in a plane of a circle or sphere that intersects the circle/sphere in exactly one point Chord • A segment whose endpoints lie on a circle or a sphere • A diameter is a chord that contains the center of the circle – Longest chord of a circle Secant • A line in a plane of a circle or sphere that intersects a circle in 2 points • A line that contains a chord Congruent Circles • Circles that have the same radii but not necessarily the same center Concentric Circles • Circles that lie in the same plane and have the same center but not the same radii • Ex: rock thrown in water Polygons and Circles • A polygon is inscribed in a circle or the circle is circumscribed about the polygon when each vertex of the polygon lies on the circle When 2 circles do not touch • Can construct 4 common tangents – 2 External Tangents – 2 Internal Tangents • Internal line of center of circle When 2 circles touch externally • Can construct 3 tangents – 2 external tangents – 1 internal tangent When 2 circles intersect each other at 2 points (overlap) • Can construct 2 external tangents When 2 circles touch internally • Can construct only one tangent – Intersects both 2 concurrent circles • Can NOT construct any common tangent – Zero 9.2 Tangents Tangent Perpendicular Theorem • If a line is tangent to a circle, then the line is perpendicular to the radius drawn to the point of tangency • Angle <ATO = 90 Corollary • Tangents to a circle from a point outside the circle are congruent ≅ • Prove by H-L and CPCTC C. Tangent Perpendicular Theorem • If a line is perpendicular to the radius at its outer end point, then the line is tangent to the circle B Name each of the following: Two radii: BO, OD A secant : AB Two chords: AB, BD A diameter : BD A tangent: ED A point of tangency: D B and D are the centers of the circles. A O D A B 14 Find the length of AC E C D 7 9-3 : Arcs and Central Angles Central Angle ● An angle with its vertex at the center of the circle Arc ● An unbroken part of the circle Minor Arc ● Points in the interior of central angle ● Named by endpoints Major Arc ● 2 points & remaining points of center circle ● Named by 3 points Semicircles ● If 2 points are the endpoints of a diameter then 2 arcs are called semicircles Measure of a Semicircle ● M = 180 Measure of a minor angle = The measure of its central angle Measure of a Major Arc ● 360 – measure of minor arc Adjacent Arcs ● Arcs that have exactly one point in common Arc Addition Postulate ● The measure of the arc formed by 2 adjacent arcs is the sum of the measures of these 2 arcs Congruent Arcs Arcs, in the same circle, or in congruent circles that have equal measures Th. 9.3 In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are ≅ Problems 9-3 Find measure of c ent ral angle 1 150 At 11 o'c loc k the hands of a clock form an angle of ____ ? 1 T he hands of a c loc k form a 120 angle at ___ o'c loc k and at ___ o'c loc k. mCB 60 M<1 ? M<2 ? 70 ? ? ? 56 ? ? ? 25 ? ? x 9.4 Arcs and Chords: •Theorem 9.4 –In the Same Circle or in congruent circles congruent arcs have congruent chords –In the Same Circle or in congruent circles, congruent chords have congruent arcs •Theorem 9.5 –A diameter that is perpendicular to a chord bisects the chord & its arc •Theorem 9.6 –In the same circle or in congruent circles, chords equally distant from the center are congruent –In the same circle or in congruent circles, congruent chords are equally distant from the center Practice Problems 9-4 D B O N M E 13 C PQ = 24; OM = ____? BC = 18; OM = 12 ON=10 ; DE = ___? 9.5 Circles – Inscribed Angles Inscribed angle : • Angle with vertex on circle and sides which are chords of the circle. Intercepted Arc • The points on the circle in the interior of an angle of the circle. Theorem 9-7 • The measure of the inscribed angle is half as much as the intercepted arc Corollary 1: • If two inscribed angles intercept the same arc or congruent arcs, then the angles are congruent Example … Find X : • Since X is an inscribed arc, then the measure of the angle is ½ the measure of the arc • So, x = 54 Try it! Find X: Corollary 2: • An angle inscribed in a semicircle is a right angle Corollary 3: • The opposite angles of an inscribed quadrilateral are supplementary Corollary 4: • The angle formed by a tangent and a chord equal 1/2 the measure of the intercepted arc 9.6 Other Angles Angle Formed by 2 chords: • Is the average of the 2 arcs • M<X = (mBD + mCA) ÷ 2 Angle Formed by 2 secants • Is the difference of the 2 arcs • m<X = (mAB – mCD) ÷ 2 Angle formed by 2 tangents • • Is (major arc – minor arc) ÷ 2 M<X = (mACB – mAB) ÷ 2 A Angle formed by a secant & a tangent • M<X = (mAD – mAC) ÷ 2 Example Problems… Find X: 9.7 Circles & Lengths of Segments Theorem 9.11 • RxQ=TxS Theorem 9.12 • DE x ME = FE x NE Theorem 9.13 • R x S = T2 • NR x KR = SR2 S Q R T S R T • Try it! Find X: