Download Methods of Mathematical Physics – Graphs of solutions to wk 6 HW

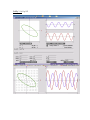
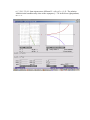
Methods of Mathematical Physics – Graphs of solutions to wk 6 HW due wk 7, fall 2010
DiffEq & Mechanics HW #3, Friday 12 Nov. 2010, E.J.Zita
Mathematica plots generated in 3DM6.nb, saved as 3DM6.pdf
Slope fields generated with DiffEq disk.
DiffEq Ch.2 # 17 (p.198)
k+ = -0.27
eigenlines
k - = -3.73
1.0
0.8
0.6
0.4
1
0.2
0.2
1
2
3
4
5
0.4
0.6
0.8
1.0
6
0.2
1
2
y+(t) (blue) and v+(t) (purple)
3
(generated with Mathematica)
y-(t) (blue) and v-(t) (purple)
To use the LinearPhasePortraits software on the DiffEq disk (to generate third plot), we
wrote the system as two first-order equations and input the matrix elements into the software.
d2y
dy
Recall the problem we did in class:
 p  qy  0 can be rewritten:
2
dt
dt
dy
v
2
dv d y
dy
dt
Let v=dy/dt, then
. In Matrix form,

  p  qy   pv  qy and
dv
dt dt 2
dt
  pv  qy
dt
 dy 
 dy 
 dt   0
 dt   0 1  y 
1  y 
 
  . For #17, p=4 and q=1, so the matrix is    
  .
 dv   q  p  v 
 dv   1 4  v 
 
 
 dt 
 dt 
Put that into the LinearPhasePortraits software: It gives the right eigenvalues, and both
straight line solutions are correctly drawn as sinks (with solutions tending toward zero.)
DiffEq 3.1 #11 p.253
DE 3.2 #5 p.271 – Looks like this is overdamped or critically damped.
3.3 # 5 p.287: Sketch the phase portrait for 3.2 #7 (p.271)
3.3#9: Sketch the solution curves for 3.2 # 11 (p.272) (using HPGSystemSolver)
We found for eigenvalue = 2: eigenvector (1, -2)
for eigenvalue = - 3: eigenvector (2, 1)
(a) x(0), y(0) = (1,0): The solution with this initial condition stays close to the asymptote
y = -2x in the lower right quadrant, as t → ∞.
(b) 3.3#9 / 3.2 #11 Same eigenvectors, different IC: x(0), y(0) = (0,1): The solution with
this initial condition stays close to the asymptote y=-2x in the upper left quadrant, as t → ∞.
(c) 3.3#9 / 3.2 #11 Same eigenvectors, different IC: x(0), y(0) = (1,-2): The solution
with this initial condition stays close to the asymptote y = -2x in the lower right quadrant,
as t → ∞.
Mechanics Ch.3.24: F = x – x3 yields system of equations dx/dt = y, y = x – x3 .
Get phase plots for this non-ideal oscillator with with HPGsystem solver:
If we start at t=0 with (x,y) = (1,0), we get no oscillations.
If we start at t=0 with (x,y) = (0,1), we do get oscillations, slightly shifted.