Download Perpendicular Bisector (con`t)

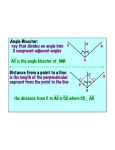
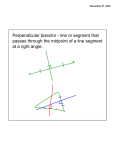
Relationships in Triangles
Bisectors, Medians, and Altitudes
Section 6.1 – 6.3
Students Should Begin Taking Notes At Screen 4!!
1
Objectives of this lesson


To identify and use perpendicular
bisectors & angle bisectors in
triangles
To identify and use medians &
altitudes in triangles
2
Vocabulary





Perpendicular Bisectors
Angle Bisectors
Medians
Altitudes
Points of Concurrency
3
STUDENTS SHOULD BEGIN TAKING NOTES HERE!
Perpendicular bisector
• A line segment or a ray that passes through the
midpoint of a side of a triangle & is ⊥ to that side.
In the picture to
the right, the
red line segment
is the ⊥ bisector
4
Perpendicular Bisector (con’t)
• For every triangle there are 3 perpendicular bisectors
• The 3 perpendicular bisectors intersect in a common
point named the circumcenter.
In the picture to the right
point K is the circumcenter.
5
Perpendicular Bisector (con’t)
•Any point on the perpendicular bisector of a segment is equidistant
from the endpoints of the segment
•Any point equidistant from the endpoints of a segment lies on the
perpendicular bisector of the segment
6
Angle Bisector

A line, line segment or ray that bisects an interior angle
of a triangle
In the picture to the right,
the red line segment is the
angle bisector. The  arc
marks show the 2  angles
that were formed when the
angle bisector bisected the
original angle.
7
Angle Bisector (con’t)
• For every triangle there are 3 angle bisectors.
• The 3 angle bisectors intersect in a common point named
the incenter
In the picture to the
right, point I is the
incenter.
8
Angle Bisector (con’t)


Any point on the angle bisector is equidistant from the
sides of the angle.
Any point equidistant from the sides of an angle lies on
the angle bisector.
9
Median
A line segment whose endpoints are a vertex of a
triangle and the midpoint of the side opposite the
vertex.
In the picture to the
right, the blue line
segment is the median.
10
Median (con’t)


For every triangle there are 3 medians
The 3 medians intersect in a common point named the
centroid
In the picture to the
right, point O is the
centroid.
11
Altitudes
A line segment from a vertex to the line containing the
opposite side and perpendicular to the line containing that
side.
In the picture above, ∆ABC is an
obtuse triangle & ∠ACB is the obtuse
angle. BH is an altitude.
12
Altitudes
(con’t)
• For every triangle there are 3 altitudes
• The 3 altitudes intersect in a common point called
the orthocenter.
In the picture to
the right, point H
is the orthocenter.
13
Points of Concurrency
Concurrent Lines
3 or more lines that intersect at a common point
Point of Concurrency
The point of intersection when 3 or more lines intersect.
Type of Line Segments
Perpendicular Bisectors
Angle Bisectors
Median
Altitude
Point of Concurrency
Circumcenter
Incenter
Centroid
Orthocenter
14
Points of Concurrency (con’t)
Facts to remember:
1. The circumcenter of a triangle is equidistant from the
vertices of the triangle.
2. Any point on the angle bisector is equidistant from the
sides of the angle (Converse of #3)
3. Any point equidistant from the sides of an angle lies on
the angle bisector. (Converse of #2)
4. The incenter of a triangle is equidistant from each side
of the triangle.
5. The distance from a vertex of a triangle to the centroid
is 2/3 of the median’s entire length. The length from the
centroid to the midpoint is 1/3 of the length of the
median.
15
Points of Concurrency (con’t)
16
Facts To Remember & MEMORIZE!
1. Perpendicular Bisectors
1. …form right angles AND
2  lines segments
2. Angle Bisectors
2. …form 2  angles
3. Medians
3. …form 2  line segments
4. Altitudes
4. … form right angles
17
The End
(Finally!)
18