Download Section 5.3: Use Angle Bisectors in Triangles

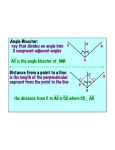
Section 5.3: Use Angle
Bisectors in Triangles
Section 5.4: Use Medians and
Altitudes
Section 5.3: Use Angle Bisectors in Triangles
Vocabulary:
 Angle bisector - divides an angle into two congruent
adjacent angles
 Incenter – where all of the angle bisectors of a
triangle intersect. The incenter is equidistant from
all of the sides of the triangle.
Section 5.3: Use Angle Bisectors in Triangles
Theorems:
 Angle Bisector Theorem

If a point is on the bisector of an angle, then it is equidistant from the
two sides of the angle
 Converse of the Angle Bisector Theorem

If a point is equidistant from the sides of the angle, then it is on the
angle bisector
 Concurrency of Angle Bisectors of a Triangle

The angle bisectors intersect at a point that is equidistant from all
sides of the triangle (incenter)
Section 5.3: Use Angle Bisectors in Triangles
Things to remember:
 The angles cut by the angle bisector are congruent
 The distance from the incenter to any side of the triangle
is the same
 Use the Pythagorean Theorem as needed to find any
missing lengths
 Practice problems: Workbook Pg 289 # 1 - 10
Section 5.4: Use Medians and Altitudes
Vocabulary:
 Median of a triangle – segment from a vertex to the
midpoint of the side opposite
 Centroid – where all of the medians of a triangle
intersect (ALWAYS inside the triangle)
 Altitude of a triangle – perpendicular segment from
a vertex to the opposite side (or the line that contains
the opposite side)
 Orthocenter – where all of the altitudes of a triangle
intersect (may be inside or outside the triangle)
Section 5.4: Use Medians and Altitudes
Theorems:
 Concurrency of the Medians of a Triangle
 The medians of a triangle intersect at a point that is two-thirds
of the distance from each vertex to the midpoint of the
opposite side (centroid)
 Concurrency of the Altitudes of a Triangle
 The altitudes of a triangle intersect at a point (orthocenter)
Section 5.4: Use Medians and Altitudes
Things to remember:
 Medians cut opposite side into congruent segments
 Altitudes MUST be perpendicular to the side opposite (or
the line containing the side…extend the side out for
obtuse triangles)
 Centroid is 2/3 of the distance from the vertex and 1/3 of
the distance from the side
 Practice problems: Workbook Pg 294 # 1 - 16
What is coming up…
 Thurs 3/5
 Sections 5.7, 5.8, and 5.9
 Wednesday 3/11
 Work on task in class
 Fri 3/6
 Thursday 3/12
 Sections 5.10, 5.11, and 5.12
 Review for Ch 5 Test
 Monday 3/9
 Review for Benchmark
 Tuesday 3/10
 3rd Quarter Benchmark
 Friday 3/13
 Ch 5 Test
Homework (in your book…)
Section 5.3
Page 274 # 1 – 12 and # 14 – 17
Section 5.4
Page 280 # 1 – 6 and # 10 - 24