Download NAME Date Band Angle Bisectors of a Triangle Adv Geometry

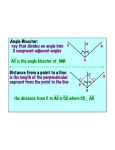
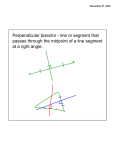
NAME
DATE
BAND
ANGLE BISECTORS OF A TRIANGLE
ADV GEOMETRY | PACKER COLLEGIATE INSTITUTE
In Geogebra, there is a angle bisector tool in this menu:
In order to properly use this tool, you have to click on the three points that create the angle. (If you
don’t, you will often see two different lines, which is a strange thing that Mr. Kinnell and Mr. Shah do
not understand.)
1. In Geogebra, draw a non-regular random-looking pentagon. Draw the angle bisectors for each angle.
How many times do the angle bisectors intersect? __________
2. (a) Do the same for a non-regular random-looking quadrilateral.
How many times do the angle bisectors intersect? __________
(b) Drag the points so that the angle bisectors intersect at the fewest number of points.
How many intersection points were you able get? __________
Draw a sketch of your quadrilateral:
3. Do the same for a non-regular random-looking triangle.
How many times do they intersect? __________
Drag the points around so the angle bisectors intersect at the greatest number of points.
How many intersection points were you able to get? _________
4. Based on your work in #3, come up with a conjecture: __________________________________
____________________________________________________________________________________
___________________________________________________________________________________.
1
5. We did something similar before, but instead of using angle bisectors of polygons, we used
perpendicular bisectors of polygons. When you did this, you found that for any triangle (this wasn’t true
for other polygons), the perpendicular bisectors always met at a single point – no matter what triangle
you drew. Then you proved it.
What was special about the point that all three perpendicular bisectors met at?
6. Try to prove this conjecture you made in #4 about angle bisectors of a triangle. If you get stuck, there is
a diagram and a hint on the next page that can help y’all.
2
Hint: You want to show that for any triangle, all three angle bisectors will intersect at a single point.
Well, you know two angle bisectors intersect at a single point. So what you really need to do is figure out
how you know with certainty that the third angle bisector also hits that same point. Here I’ve drawn the
angle bisectors for angles A and C.
Why do I know the angle bisector for B will intersect at the same place that the other two hit?
Need another hint? Go back and review the worksheet titled “Angles and Circles.” Use what you learned there!
3
Need one more hint? Okay, go back and review how we proved that the three perpendicular bisectors of a
triangle will always meet at a single point. A similar argument (but it isn’t the same argument) can be used to
prove this.
4