Download Work and Kinetic Energy - University of Utah Physics

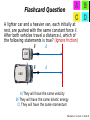
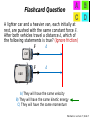
Lecture 07: Work and Kinetic Energy
Physics 2210
Fall Semester 2014
Announcements
●
Schedule next few weeks:
●
9/08 – Unit 3
●
9/10 – Unit 4
●
9/15 – Unit 5 (guest lecturer)
●
9/17 – Unit 6 (guest lecturer)
●
9/22 – Unit 7, Exam Review
●
work practice exam in discussion
●
9/24 – Exam 1, Units 1-6
●
9/25 – Unit 7 HW due
Unit 7: Prelecture Feedback
●
●
●
●
●
Review dot product
Derive relation between work and K.E.
Review all checkpoint problems
“Work” through examples
Why is “work” relevant?
Mechanics Lecture 6, Slide 3
The Dot (also “scalar”, “inner”)
Product of Two Vectors
Mechanics Lecture 7, Slide 4
Work-Kinetic Energy Theorem
The net work done on a body is equal
to the change in kinetic energy of the body
Formal definition of work
(“Force times distance” generalized)
Formal definition of kinetic energy
Mechanics Lecture 7, Slide 5
Flashcard Question
A lighter car and a heavier van, each initially at
rest, are pushed with the same constant force F.
After both vehicles travel a distance d, which of
the following statements is true? (Ignore friction)
F
d
car
F
d
van
A) They will have the same velocity
B) They will have the same kinetic energy
C) They will have the same momentum
Mechanics Lecture 7, Slide 6
Flashcard Question
A lighter car and a heavier van, each initially at
rest, are pushed with the same constant force F.
After both vehicles travel a distance d, which of
the following statements is true? (Ignore friction)
F
d
car
F
d
van
A) They will have the same velocity
B) They will have the same kinetic energy
C) They will have the same momentum
Mechanics Lecture 7, Slide 7
Example: I lift an object of mass m, starting
at rest, and place it at rest on a table of
height h.
1)
2)
3)
4)
What is the work done by gravity?
What is the work done by me?
What is the change in kinetic energy?
Do the answers above depend on the
path taken by the object?
Work-Kinetic Energy Theorem
If there are several forces acting then W is
the work done by the net (total) force:
WNET = ∆K
= W1 + W2 + ...
You can just add up the
work done by each force
WNET = WTOT
Mechanics Lecture 7, Slide 9
Example: I drop an object of mass m, from a
height h, starting at rest. What is its speed v
when it hits the floor...
a) As calculated by 1D kinematics?
b) As calculated by the Work-KE theorem?
CheckPoint
Three objects having the same
mass begin at the same height,
and all move down the same
vertical distance H. One falls
straight down, one slides down a
frictionless inclined plane, and
one swings on the end of a
string.
H
Free Fall
Frictionless incline
A) Free Fall
String
B) Incline C) String
In which case
does the
object have
the biggest
net work
done on it by
all forces
during its
motion?
D) All the same
Mechanics Lecture 7, Slide 11
CheckPoint
Three objects having the same
mass begin at the same height,
and all move down the same
vertical distance H. One falls
straight down, one slides down a
frictionless inclined plane, and
one swings on the end of a
string.
H
Free Fall
Frictionless incline
A) Free Fall
String
B) Incline C) String
In which case
does the
object have
the biggest
net work
done on it by
all forces
during its
motion?
D) All the same
Mechanics Lecture 7, Slide 12
Flashcard Question
Three objects having the same mass begin
at the same height, and all move down the
same vertical distance H. One falls straight
down, one slides down a frictionless inclined
plane, and one swings on the end of a string.
What is the relationship between their
velocities when they reach the bottom?
H
Free Fall
Frictionless incline
A) vf > vi > vs
B) vf > vs > vi
String
C) vf = vs = vi
Mechanics Lecture 7, Slide 13
Flashcard Question
Three objects having the same mass begin
at the same height, and all move down the
same vertical distance H. One falls straight
down, one slides down a frictionless inclined
plane, and one swings on the end of a string.
What is the relationship between their
velocities when they reach the bottom?
H
Free Fall
Frictionless incline
A) vf > vi > vs
B) vf > vs > vi
String
C) vf = vs = vi
Mechanics Lecture 7, Slide 14
CheckPoint
A car drives up a hill with constant speed.
Which statement best describes the total
work WTOT done on the car by all forces as it
moves up the hill?
v
A) WTOT > 0
B) WTOT = 0
C) WTOT < 0
Mechanics Lecture 7, Slide 15
CheckPoint
A car drives up a hill with constant speed.
Which statement best describes the total
work WTOT done on the car by all forces as it
moves up the hill?
v
A) WTOT > 0
B) WTOT = 0
C) WTOT < 0
Mechanics Lecture 7, Slide 16
CheckPoint
A box sits on the horizontal bed of a moving
truck. Static friction between the box and the
truck keeps the box from sliding around as the
truck drives.
µS
a
The work done on the box by the static frictional
force as the truck moves a distance D is:
A) Positive
B) Negative
C) Zero
Mechanics Lecture 7, Slide 17
CheckPoint
A box sits on the horizontal bed of a moving
truck. Static friction between the box and the
truck keeps the box from sliding around as the
truck drives.
µS
a
The work done on the box by the static frictional
force as the truck moves a distance D is:
A) Positive
B) Negative
C) Zero
Mechanics Lecture 7, Slide 18
Work done by a Spring
Physics 211 Lecture 7, Slide 19
I am confused about the positive work and negative work and
also the positive and negative forces for the spring problems.
Use the formula to get the magnitude of the work
Use a picture to get the sign (look at directions)
In this example the spring does negative work since F and ∆x are
in opposite direction. The axes don’t matter.
Physics 211 Lecture 7, Slide 20
Example: Simple Gravitational Orbit
A space telescope of mass
10,000 kg is in a stable orbit
above the Earth at an altitude
h = 3,630 km. The radius and
mass of the Earth are
RE = 6,370 km and
ME = 6.0x1024 kg, respectively.
Newton's gravitational
constant is
G=6.672x10-11 Nm2/kg2.
(a) what is the acceleration of
the space telescope? (b) if the
telescope's mass were to
increase, what would need to
happen to its speed in order to
maintain the same orbit?
Example
I move an object from the surface of the
Earth to a height of one Earth radius above
the Earth, and to a position on the far side
of the Earth from the launch position. The
object is at rest with respect to the Earth
before and after the move.


What is the work that I must do on the object?
If the object were instead moved to “infinity” (or at
least very, very far away), what work must I do?
Exam Details
●
Coverage: Units 1-6
●
1D Kinematics
●
2D Kinematics
●
Relative and Circular Motion
●
Newton's Laws
●
Free Body Diagrams
●
Friction
●
Problem types: Multiple choice & workout.
●
Study recommendations:
●
●
Review homework
●
See practice exam on course webpage
●
Solve problems, problems, problems...
Allowed materials
●
Calculator (not on cell phone)
●
Straightedge
●
Blue or black pen required for regrade
●
Equation sheet will be provided
1D Kinematics
●
●
●
Precise “physicist”
definitions of words you
use every day.
Differential and integral
representations.
Graphical representation.
2D Kinematics
●
●
●
●
Generalize 1D
kinematics to 2 or 3D
Vectors, vector addition
and subtraction.
Projectile motion:
●
Horizontal constant v
●
Vertical constant a
Horizontal and vertical
independent
Relative and
Circular Motion
●
●
●
Kinematics may be
described in different
coordinate systems.
These systems may be
in relative motion.
Circular motion at
constant linear speed
is accelerated motion.
Acceleration is
towards center of
circle.
Newton's Laws
●
●
●
2nd Law: define force
in terms of mass and
acceleration.
1st Law: Special case
of 2nd. “Inertia”
3rd Law: forces come
in pairs, but act in
opposite directions.
Free-Body
Diagrams
●
●
Tool for generating
equations that relate
knowns to unknowns.
Useful for many types of
forces
●
Support forces
●
Spring forces
●
Gravity (near Earth
and far from Earth).
●
Friction
Friction
●
●
Contact force between
two objects. Parallel to
adjoining surface.
Two types:
●
Kinetic (moving)
●
Static (at rest)