* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Best Credit Data Bond Analytics Calculation Methodology Created by
Internal rate of return wikipedia , lookup
Securitization wikipedia , lookup
Financialization wikipedia , lookup
Modified Dietz method wikipedia , lookup
Business valuation wikipedia , lookup
Financial economics wikipedia , lookup
Interest rate ceiling wikipedia , lookup
Greeks (finance) wikipedia , lookup
United States Treasury security wikipedia , lookup
Yield curve wikipedia , lookup
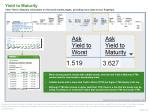
Best Credit Data Bond Analytics Calculation Methodology Created by: Pierre Robert CEO and Co-Founder Best Credit Data, Inc. 50 Milk Street, 17th Floor Boston, MA 02109 Contact Information: [email protected] 1-978-502-2792 Last updated: March 1, 2016 YieldtoMaturity Theyieldtomaturityformulaisusedtocalculatetheyieldonabondbasedonitscurrent priceonthemarket.Theyieldtomaturityformulalooksattheeffectiveyieldofabond basedoncompoundingasopposedtothesimpleyieldwhichisfoundusingthedividend yieldformula. Noticethattheformulashownisusedtocalculatetheapproximateyieldtomaturity.To calculatetheactualyieldtomaturityrequirestrialanderrorbyputtingratesintothe presentvalueofabondformulauntilP,orPrice,matchestheactualpriceofthebond.Some financialcalculatorsandcomputerprogramscanbeusedtocalculatetheyieldtomaturity. The yield to maturity is found in the present value of a bond formula: For calculating yield to maturity, the price of the bond, or present value of the bond, is already known. Calculating YTM is working backwards from the present value of a bond formula and trying to determine what r is. Example of Yield to Maturity Formula The price of a bond is $920 with a face value of $1000 which is the face value of many bonds. Assume that the annual coupons are $100, which is a 10% coupon rate, and that there are 10 years remaining until maturity. This example using the approximate formula would be After solving this equation, the estimated yield to maturity is 11.25%. YieldtoWorst(YTW) Typicallyusedforcallablebonds.Ifabondiscallablebeforeitsmaturitydate,youwill comparetheyieldtoeachcalldateandcallpriceaswellasmaturitydateandpriceandthe lowestyieldingdateisthe(YTW). Best Credit Data, Inc. 50 Milk Street, Boston MA, 02109 www.bestcreditanalysis.com (YTW)Steps: Step1 Notethepriceyoupaidforthebond,includingwhatpercentageofitsfacevalueyoupaid andhowmanyyearsremainuntilthebond'smaturitydate. Step2 Writedownandsetasideallcalldatesforacallablebond. Step3 Assume,forthesakeofexplanation,thatinterestrateswillremainthesame.Foreveryyear thatremainsbeforethematuritydate,dividetheanticipatedyearlyinterestpaymentbythe amountofmoneyyoupaidforthebondmultipliedby100.Thiscalculationrepresentsthe percentageofinterestyouwillearnforeachyearandcalldate.Ifyouplantoreinvestthe interesteveryyear,calculateanewyearlyinterestpaymenteveryyear.Markwhichyears arecalldatesandnotetheanticipatedinterestpercentages. Step4 Subtracttheamountyoupaidforthebondfromitsfacevaluetodeterminetheanticipated face-valueearnings,whichwillbeidenticalforeachcalldateorthematuritydate.Divide theseearningsbythebond'sfacevalueandthenmultiplyby100. Step5 Combinetheface-valuepercentagewiththeinterestpercentageforeachcalldate.Search forthecalldatewiththelowesttotalpercentage,whichistheyield-to-worstdate. Best Credit Data, Inc. 50 Milk Street, Boston MA, 02109 www.bestcreditanalysis.com Modified Duration Modified duration is a formula that expresses the measurable change in the value of a security in response to a change in interest rates. Calculated as: Where: n = number of coupon periods per year YTM = the bond's yield to maturity. Effective Duration Effective duration is a duration calculation for bonds with embedded options. Effective duration takes into account that expected cash flows will fluctuate as interest rates change. Effective duration can be estimated using modified duration if the bond with embedded options behaves like an option-free bond. This behavior occurs when exercise of the embedded option would offer the investor no benefit. As such, the security's cash flows cannot be expected to change given a change in yield. For example, if existing interest rates were 10% and a callable bond was paying a coupon of 6%, the callable bond would behave like an option-free bond because it would not optimal for the company to call the bonds and re-issue them at a higher interest rate. Z-spread TheZero-volatilityspread(Z-spread)istheconstantspreadthatwillmakethepriceofa securityequaltothepresentvalueofitscashflowswhenaddedtotheyieldateachpointon thespotrateTreasurycurvewhereacashflowisreceived.Inotherwords,eachcashflowis discountedattheappropriateTreasuryspotrateplustheZ-spread. Best Credit Data, Inc. 50 Milk Street, Boston MA, 02109 www.bestcreditanalysis.com Macaulay Duration The Macaulay duration is the weighted average term to maturity of the cash flows from a bond. The weight of each cash flow is determined by dividing the present value of the cash flow by the price, and is a measure of bond price volatility with respect to interest rates. Macaulay duration can be calculated by: Key Rate Duration Key rate duration is holding all other maturities constant, this measures the sensitivity of a security or the value of a portfolio to a 1% change in yield for a given maturity. The calculation is as follows: Where: P- = Security's price after a 1% decrease in yield P+ = Security's price after a 1% increase in yield P0 = Security's original price There are 11 maturities along the Treasury spot rate curve, and a key rate duration is calculated for each. The sum of the key rate durations along a portfolio yield curve is equal to the effective duration of the portfolio. Best Credit Data, Inc. 50 Milk Street, Boston MA, 02109 www.bestcreditanalysis.com Convexity Convexity is a measure of the curvature in the relationship between bond prices and bond yields that demonstrates how the duration of the bond changes as the interest rate changes. Convexity is used as a risk-management tool, and helps to measure and manage the amount of market risk to which a portfolio of bonds is exposed. In the example above, Bond A has a higher convexity than Bond B, which means that all else being equal, Bond A will always have a higher price than Bond B as interest rates rise or fall. As convexity increases, the systemic risk to which the portfolio is exposed increases. As convexity decreases, the exposure to market interest rates decreases and the bond portfolio can be considered hedged. In general, the higher the coupon rate, the lower the convexity (or market risk) of a bond. This is because market rates would have to increase greatly to surpass the coupon on the bond, meaning there is less risk to the investor. Best Credit Data, Inc. 50 Milk Street, Boston MA, 02109 www.bestcreditanalysis.com Option-Adjusted Spread (OAS) Definition Option-adjusted spread (OAS) is the spread relative to a risk-free interest rate, usually measured in basis points (bp), which equates the theoretical present value of a series of uncertain cash flows of an instrument to its current market price. OAS can be viewed as the compensation an investor receives for assuming a variety of risks (e.g. liquidity premium, default risk, model risk), net of the cost of any embedded options. General Applications 1. Evaluation of an interest-sensitive fixed-income security (in other words, a security whose future redemption date and payment stream are influenced by interest rates through the presence of an implicit embedded option). For example, is a 50 bp OAS appropriate for an A-rated asset? 2. Facilitates comparison of assets. For example, is a AAA-rated asset at 90 bp over the Treasury curve a better value than a B-rated asset with a 600 bp spread? 3. Profitability analysis. For example, keep OAS constant and see how price varies as various factors are changed. Or, keep price constant and see how a change in various factors impacts the OAS. 4. Product pricing. For example, when discounting interest-sensitive cash flows, what is the appropriate spread over the risk-free interest rate that compensates the company for the risks of the product? 5. Firm valuation or valuation of a book of business. For example, when discounting interest-sensitive cash flows, what spread should be added to the risk-free interest rate in order to compensate the buyer for the risks inherent in the firm or book? Calculating OAS 1. Interest rate scenarios are generated stochastically, using a model consistent with the current term structure and assumed level of volatility. 2. Free cash flows, reflecting interest-sensitive contractual features, are calculated at each time step along each interest rate path. 3. The free cash flows are discounted at the risk-free interest rate plus a spread (the OAS) to determine a value at time zero for each path. 4. An average of the path wise values is calculated. 5. Steps 3 and 4 are repeated, and the OAS is solved for which equates the average of the path wise values to the current market price. Strengths 1. Allows explicit measurement and representation of risks when pricing products. 2. Stochastic valuation provides a better representation and range of the modeled risk. 3. Stochastic analysis captures the effect of yield curve shape on interest-sensitive variables and reflects the possibility interest rates will vary in the future. Weaknesses 1. Measure is contingent on quality of model and assumptions. 2. Market price may not be available. 3. Only OAS’s of securities with similar “embedded options” can be compared. 4. Need for many scenarios may be time-consuming. Best Credit Data, Inc. 50 Milk Street, Boston MA, 02109 www.bestcreditanalysis.com