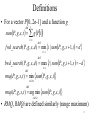Download v - Researchmap

Succinct Data Structures
Kunihiko Sadakane
National Institute of Informatics
Range Min-Max Trees [5]
• In existing succinct data structures for trees, for each
operation to be supported, a new index is added.
• The o(n) term cannot be ignored.
– The recursive method [6] uses 3.73n bits to support
only findopen, findclose, enclose.
• It is preferable if various operations can be
supported by an index
2
Definitions
• For a vector P[0..2n-1] and a function g
t
sumP, g , s, t    g Pi 
def
is
fwd_search( P, g , s, d )  min i | sumP, g , s  1, i   d 
def
is
bwd_search( P, g , s, d )  max i | sumP, g , i  1, s   d 
def
is
rmq( P, g , s, t )  min sumP, g , s, i 
def
s i t
rmqi( P, g , s, t )  arg min sumP, g , s, i 
def
s i t
• RMQ, RMQi are defined similarly (range maximum)
3
How to support operations on
balanced parentheses sequence
• Lemma: Let  be a function s.t. (() = 1, ()) = 1
findclose ( P, i )  fwd_search( P,  , i,1)
findopen( P, i )  bwd_search( P,  , i,0)  1
enclose ( P, i )  bwd_search( P,  , i,2)  1
level_ancestor ( P, i, d )  bwd_search( P,  , i, d  1)  1
enclose
findclose
P (()((()())())(()())())
E 1212343432321232321210
4
Implementing rank/select
• Let ,  be functions s.t.  (0)=0,  (1)=1,  (0)=1,
 (1)=0
rank1 ( P, i )  sum( P,  ,0, i )
select 1 ( P, i )  fwd_search( P,  ,0, i )
rank0 ( P, i )   sum( P, ,0, i )
select 0 ( P, i )  fwd_search( P, ,0,i )
• rank/select and parentheses operations can be
handled in a unified manner.
5
Range Min-Max Tree
• Divide the excess array E into blocks of length s
• Each leaf of range min-max tree corresponds to a
block, and stores min/max values in the block.
• Internal nodes have l children and stores min/max
values of the children. 0/4
1/4
1/3
0/2
m/M 1/2 2/4 3/4 2/3 1/3 2/3 1/2 0/0
E 1212343432321232321210
(()((()())())(()())())
s=l=3
6
Properties of Range Min-Max Trees
• Each node corresponds to a range of the array.
• Any range of the array is represented by a disjoint
union of O(lh) ranges corresponding to internal
nodes and at most two ranges corresponding to
leaves.
0/4
(h: tree height)
1/4
1/3
0/2
m/M 1/2 2/4 3/4 2/3 1/3 2/3 1/2 0/0
E 1212343432321232321210
(()((()())())(()())())
s=l=3
7
Properties of Excess Array
• For each i, E[i+1] = E[i]1 or E[i]+1
• Let the min/max of E[u,v] be a and b, then
in the range all integers e s. t. a  e  b exist, and
other values do not exist.
• In a range of length l, the difference between min
and max
1 is at most l1.
–
⇒ values can be stored in fewer bits
3
2
4
5 6
11
8
7
9
10
1 2 3 4 5 6
7
8 9 10
11
P (()((()())())(()())())
E 1212343432321232321210
8
Computation of fwd_search(E,i,d)
• Divide the range E[i+1,N1] (N: array length)
• Scan the divided ranges from left to right to find the
range containing E[i]+d
• O(lh+s) time
0/4
1/4
1/3
0/2
m/M 1/2 2/4 3/4 2/3 1/3 2/3 1/2 0/0
E 1212343432321232321210
(()((()())())(()())())
9
The case the array is short (polylog)
• Let w be the word length (bits) of CPU
• Lemma
If N < wc, fwd_search is done in O(c2) time, and
the data structure size is N + O(Nc/w) + exp(w) bits.
• Proof
Excess values are between wc and wc ⇒ O(c log w)
bits. w/(c log w) values can be read simultaneously.
If the branching factor l of the range min-max tree
is w/log w, ⇒ the hight of the tree is O(c).
Searching a child takes O(c) time.
10
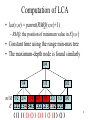
Computation of LCA
• lca(v,w) = parent(RMQ(v,w)+1)
– RMQ: the position of minimum value in E[v,w]
• Constant time using the range min-max tree
• The maximum-depth node is found similarly
0/4
1/4
1/3
0/2
m/M 1/2 2/4 3/4 2/3 1/3 2/3 1/2 0/0
E 1212343432321232321210
(()((()())())(()())())
11
Computation of Degree
• Let [v,w] be the range of E corresponding to a node
v
• deg(v) = (# of minimum values in E[v+1,w1])
• In each node of the range min-max tree, store the
number of minimum values in the range.
1
• i-th child is also found.
2
2
1
1
2
2
1
1
2
2
1
E 1212343432321232321210
(()((()())())(()())())
12
The case the array is long
• Divide the sequence into blocks of length wc
Let M1,…, Mt, m1,…, mt be max/min values of the
blocks
• To compute fwd_search(E,i,d), if E[i]+d < (the
minimum value of the block containing i), the block
containing the answer is the first block j with
mj < E[i]+d
13
Other Queries
• RMQ is done by the sparse table algorithm
– Because the number of blocks is small (n/wc),
the space can be ignored.
• Theorem: There exists a data structure supporting all
known operations on ordered trees in O(1) time
using 2n + O(n/log n) bits.
14
Further Recuding the Space
• Use “Succincter” [7]
• augmented B-tree
– B-tree for array A[1..n]
– For each node, a value is added
– Values are computed from those of child nodes and
subtree size
• Range Min-Max Tree is an augmented B-tree
• Theorem: 2n + O(n/logc n) bits
(c > 0 is an arbitrary constant.)
15
Applications of Ordered Trees
• An abstract data type for “dictionary”
• A data structure D is called dictionary if for a set S
5
and a key k, it supports
– Search(D, k): returns Yes iff k  S
– Insert(D, x): adds x to S
– Delete(D, x): removes x from S
8
1
7
• A binary search tree is used as a dictionary.
– Any balanced binary search tree supports the above
operations in O(log n) time for a set of n elements.
– We assume that element comparison is done in O(1) time.
16
Tries
•
•
•
•
Trie is a data structure for storing a set of strings.
A node has at most  children (: alphabet size)
Each edge is labeled a character c
c
d
The concatenation of characters on edges
from the root to a node coincides with a
o
the string represented by the node
b
t
g
c
A Trie for S = {cab, cat, do, doc, dog}
17
Compressed Tries
• Compressed Tries are obtained from standard Tries
by compressing chains of redundant nodes
– redundant node = a node with only one child
– #nodes  #leaves1
• An edge represents a string
b
c
a
t
d
o
g
c
S = {cab, cat, do, doc, dog}
18
Operations on Trees
• Binary search trees
– left(v), right(v): returns the left/right child node of v
– key(v): returns the key stored in node v
• Tries
– child(v, c): returns a child w of v with edge label c
– key(v): returns the key stored in node v
• Compressed tries
– child(v, c): returns a child w of v with edge label c…
– edge(w, d): returns d-th character on edge pointing to w
v
a
– key(v)
b
child(v, a) = w
edge(w, 2) = b
w
19
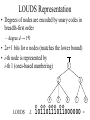
LOUDS Representation
• Degrees of nodes are encoded by unary codes in
breadth-first order
– degree d → 1d0
• 2n+1 bits for n nodes (matches the lower bound)
• i-th node is represented by
1
i-th 1 (ones-based numbering)
2
4
1
LOUDS
L
2 3
4 5 6
3
5
6
7
8
7 8
10110111011000000
20
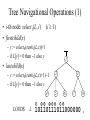
Tree Navigational Operations (1)
(i  1)
• i-th node: select1(L, i)
• firstchild(x)
– y := select0(rank1(L,x))+1
– if L[y] = 0 then 1 else y
1
• lastchild(x)
– y := select0(rank1(L,x)+1)1
– if L[y] = 0 then 1 else y
4
1
LOUDS
L
2 3
2
3
5
4 5 6
6
7
8
7 8
10110111011000000
21
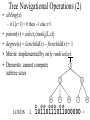
Tree Navigational Operations (2)
• sibling(x)
– if L[x+1] = 0 then 1 else x+1
•
•
•
•
parent(x) = select1(rank0(L,x))
degree(x) = lastchild(x)  firstchild(x) + 1
Merits: implemented by only rank/select
Demerits: cannot compute
1
subtree sizes
2
4
1
LOUDS
L
2 3
4 5 6
5
3
6
7
8
7 8
10110111011000000
22
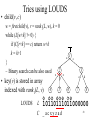
• child(v, c)
Tries using LOUDS
w = firstchild(v), r = rank1(L, w), k = 0
while (L[w+k] != 0) {
if (C[r+k] == c) return w+k
k = k+1
}
– Binary search can be also used x 2
• key(v) is stored in array
indexed with rank1(L, v)
1
LOUDS
a
1
c
3
z
a
y
4
5
2 3
4 5 6
6
7 8
7
d
8
L 10110111011000000
23
C _acxyzad
• A trie with n nodes and size- label set supporting
child(v, c) in O(log ) time is represented in
n(2+log ) + o(n) bits.
– O() time sequential search is faster for small .
• By using an auxiliary array, key(v) is performed in
O(1) time.
24
BP Representation
• Each node is represented by a pair of matching
open and close parentheses
• 2n bits for n nodes
1
• The size matches the lower bound
2
3
6
4
5
7
8
1
2
6
3
BP
P
4
5
7
8
((()()())(()()))
25
Tree Navigational Operations
•
•
•
•
parent(v) = enclose(P,v)
firstchild(v) = v + 1
sibling(v) = findclose(P,v) + 1
lastchild(v) = findopen(P, findclose(P,v)1)
1
enclose
3
2
4
5 6
11
8
7
9
findclose
1 2 3 4 5 6
7
8 9 10
11
(()((()())())(()())())
10
26
Tries using BP
• child(v, c)
w = firstchild(v)
while (w != NIL) {
if (C[rank((P, w)] == c) return w
w = sibling(w)
2
}
x
• key(v) is stored in array
indexed with rank((P, v)
BP
P
C
y
3
4
1 2 3
4
a 1 c
z
a
5
5
6
d
7
6 7
8
8
((()()())(()()))
_axyzcad
27
DFUDS Representation
• It encodes the degrees of nodes in unary codes in
depth-first order
(DFUDS = Depth First Unary Degree Sequence)
1
• Degree d ⇒ d (’s, followed by a )
• Add a dummy ( at the beginning 2
6
• 2n bits
• DFUDS is balanced
DFUDS
3
4
5
7
8
U ((()((())))(()))
1
2
3 4 5
6
7 8
28
i-th child
child (v, i )  findclose select ) rank ) (v)  1  i   1
v
U1
U2 U3
(((()(())))((())))
v
1
2
6
5
3
4
7
8
9
29
Tries using DFUDS
• child(v, c)
r = rank((U, v), k = 0
while (U[v+k] != ‘)’ ) {
if (C[r+k] == c) return child(v, k+1) a 1 c
k = k+1
2
}
x
z
y
• O() time
O(log ) is possible
DFUDS
a
3
4
5
6
d
7
8
U ((()((())))(()))
1
C
2
_acxyzad
3 4 5
6
7 8
30
References
[1] 定兼邦彦, 渡邉大輔. 文書列挙問題に対する実用的なデータ構造.
日本データベース学会Letters Vol.2, No.1, pp.103-106.
[2] Michael A. Bender, Martin Farach-Colton: The LCA Problem
Revisited. LATIN 2000: 88-94
[3] Kunihiko Sadakane: Succinct data structures for flexible text retrieval
systems. J. Discrete Algorithms 5(1): 12-22 (2007)
[4] Johannes Fischer: Optimal Succinctness for Range Minimum Queries.
LATIN 2010: 158-169
[5] Kunihiko Sadakane, Gonzalo Navarro: Fully-Functional Succinct
Trees. SODA 2010: 134-149.
[6] R. F. Geary, N. Rahman, R. Raman, and V. Raman. A simple optimal
representation for balanced parentheses. Theoretical Computer
Science, 368:231–246, December 2006.
[7] Mihai Pătraşcu. Succincter, Proc. FOCS, 2008.
31