* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Foundations of Programming Languages Seyed H. Roosta
Curry–Howard correspondence wikipedia , lookup
Falcon (programming language) wikipedia , lookup
Closure (computer programming) wikipedia , lookup
Anonymous function wikipedia , lookup
Combinatory logic wikipedia , lookup
Standard ML wikipedia , lookup
Lambda calculus wikipedia , lookup
COSC3306:
Programming Paradigms
Lecture 10: Applicative
Programming Specifications
Haibin Zhu, Ph.D.
Computer Science
Nipissing University
(C) 2003
1
The Lambda Calculus
Everything is a function.
– There are no other types---no integers, strings, lists,
booleans, etc. There is no unit (). If you want these
things, you must encode them using functions. Luckily,
functions are powerful enough to do this.
No state or side effects.
– It is purely functional. Thus we can think exclusively in
terms of the substitution model.
The order of evaluation is irrelevant.
– The lambda calculus does not specify an evaluation
order.
Only unary (one-argument) functions.
– Functions of multiple arguments are encoded by
currying.
2
Key properties of functional
programming
Lazy function evaluation, which is a mechanism that
eliminates unnecessary evaluation of functions and
includes two strategies:
– Postponing evaluation of a function until it is needed, and
– Eliminating the reevaluation of the same function more than once.
First-class objects, which means that functions are
treated like any other object in the language.
All programs and procedures are functions, which
clearly distinguishes incoming values as parameter values
from outgoing values as evaluation results.
Lack of variable and assignment, which eliminates the
concept of variable, except as a name for a value, and
assignment as an available operation.
3
Key properties (2)
Lack of loop and iteration, which means that there is no
loop and that loops are replaced by recursive calls.
Referential transparency, which is the property of a function
whereby its value depends only on the values of its
parameters, not on any previous computations, the order of
evaluation, or the execution path that led to the call. .
Dynamic Memory Environment, which is allocation and
deallocation of memory during program execution. As a
consequence, a fully dynamic environment must perform
some kind of automatic reclamation of unreachable storage.
Automatic memory management actually falls into two
categories:
– Reclamation of Storage, which is the process of reclaming
previously allocated but no longer used storage, sometimes called
garbage collection, as we discussed in Chapter 3.
– Maintaining Free Space, which is the process of maintaining the free
space available for allocation, as we discussed in Chapter 3.
4
Key properties (3)
Garbage Collection, which is the process of
keeping track of inaccessible storage and
permitting it to be reallocated.
Side-effect freedom, which is the ability to call
a function without producing side effects, that is,
without changing the internal state of the
computations. Side effects are operations that
permanently change the value of a variable or
other observable objects.
5
Lambda Calculus
A mathematical method for expressing computation by
functions and is used for studying functional
programming language concepts.
Lambda calculus gets its name from the Greek letter
lambda, .
The general form of a lambda expression, known as the
lambda function, is
– id1, id2, …, idn. expression
where the id’s are identifiers (parameters or variables)
and expression (called the body of the lambda function)
is some expression that may involve the identifiers.
6
An example
x. xx
– is a function that maps any value of x to xx and
defines a mapping from an integer number to integer
numbers, yielding the square of integer numbers. This
lambda expression can be applied as
{x. xx }(2)
– where the result of the lambda expression xx can be
deduced by replacing the parameter and evaluating
the resulting expression with 2.
7
© 2003 Brooks/Cole Publishing / Thomson Learning™
Figure 12.1 A lambda expression with evaluation value
8
Lambda notation
Lambda notation allows the definition of a
function without a name.
– For example, x. xx defines a lambda function that
maps each x in the integer domain to x2.
Generally speaking, the value of a lambda
expression such as
id1, id2, …, idn. expression (a1, a2, …, an)
when applied to arguments (a1, a2, …, an), is
given by evaluating expression, with a1
substituted for all occurrences of id1, a2
substituted for all occurrences of id2, and an
substituted for all occurrences of idn.
9
Figure 12.2 Examples of lambda funcions
10
More examples
{x. ( x x)}( 3 4) {x. ( x x)}(7) ( 7 7) 14
{x. ( x x)}( 3 4) { ( 3 4)} ( 3 4)} { 7 7}
14
In the following example, we use two arguments
with the abstraction to define a function,
replacing f with sqr, a predefined square
function, and x with 3.
{{{f. {x. (f (f x))}}sqr}3} {{x. (sqr(sqr x))}3}
(sqr(sqr 3)) (sqr 9) 81
11
Function definitions
Lambda Function
Function Name
x, y. x y
Plus
x. x x
Square
x. x 1
Successor
x. x 1
Predecessor
x, y. if x y, then x else y end Max
x. x
Identity
12
Ambiguity
The lambda expression
– x. y. f (g)
admits three possible interpretations,
illustrating the ambiguity of the lambda
calculus grammar:
– x. {y. {f (g)}},
– x. {{y. f } (g)}, and
– {x. y. f } (g).
13
Remove ambiguity
Complicating the grammar and Using
parentheses.
However, it is preferable to leave the grammar
as it is and add the convention that the function
application has the highest precedence.
Thus, by default, the interpretation of the
preceding expression is the first entry in the list.
Braces are used to override this precedence
when necessary.
14
Free and Bound Identifiers
x. x+y
– Y is a reference that is not bounded called a
free identifier.
x. x+y (5)=5+y
x, y, z. x+y+z => {x. {y. {z. (x+y+z)}}}
Free identifiers may be renamed without
changing the value of expressions within
which they occur.
15
© 2003 Brooks/Cole Publishing / Thomson Learning™
Figure 12.3 A lambda expression
with free and bound identifiers
16
Reductions
Alpha-conversion (α-conversion)
– x. E α y. E[ x → y]
( w. ( y. z) w) α ( x. ( y. z) x)
Beta-conversion(β-conversion)
– x. E1 E2 β E1 [x → E2]
(x. x +1) 5 β 5+1 6
(g. g (a. b. a)) ((a. b. f. f a b) p q)
β ((a. b. f. f a b) p q) (a. b. a)
β (b. f. f p b) q) (a. b. a)
β (f. f p q) (a. b. a)
β (a. b. a) (p q) β ( b. p) (q) β p
17
Reductions (2)
Eta-conversion(η-conversion)
– {x. E} x η E
{x. (sqr 5)} x η (sqr 5) η 25
{x. y} x η y
Gamma-conversion(δ-conversion)
– {function x y} δ function (x y)
Add 5 3 δ add(5 3) 8
P407 examples
18
The Church-Rosser Theorem
If a lambda expression M evaluates to a normal
form A via a sequence of reduction (M *A),
and another sequence of reductions takes M to
a normal form B (M *B), then some common
term N can be found such that A can be reduced
to N (A *N and B *N).
Any relation that satisfies this condition is said to
have the diamond property or the confluence
property.
19
© 2003 Brooks/Cole Publishing / Thomson Learning™
Figure 12.4 The Church-Rosser theorem
20
© 2003 Brooks/Cole Publishing / Thomson Learning™
Figure 12.5 Alternative evaluations of a lambda expression
21
Order of evaluation
No two orders of evaluation of a lambda
expression can give different normal
forms.
Normal order (call-by-name)
– Reduce the left most expression at every
stage.
Applicative order (call-by-value)
– Evaluates the function and the argument of an
application first.
22
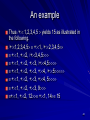
An example
Normal order:
–
–
–
–
–
–
(x. x + x + x + x) ((x. x) a)
(x. x) a + (x. x) a+ (x. x) a+ (x. x) a
a + (x. x) a+ (x. x) a+ (x. x) a
a + a+ (x. x) a+ (x. x) a
a + a+ a+ (x. x) a
a + a+ a+ a
Applicative order
– (x. x + x + x + x) ((x. x) a)
– (x. x + x + x + x) (a)
– a + a+ a+ a
23
To be continued
Principles of Functional Programming
24
Principles of Functional
Programming
A relation describes associations between
objects.
For example, consider two set of elements, X
and Y. A relation R between X and Y is
defined as a set of pairs of elements such as
{a1, b1,a2 b2, … ,an, bn}, where every
ai is a member of X and every bi is a member
of Y. Here, X is called the source domain, and
Y is called the target domain.
25
© 2003 Brooks/Cole Publishing / Thomson Learning™
Figure 12.6 A relation expressing {<x1, y1>, <x1,
y2>, <x2, y2>, <x4, y3>, <x4, y5>}
26
A relation such that there is at most one such y for
every x is said to be a function that corresponds to a
mapping from one element of X to one element of Y.
© 2003 Brooks/Cole Publishing / Thomson Learning™
Figure 12.7 A function expressing {<x1, y1>, <x2, y2>, <x3, y4>, <x4, y5>}
27
Functions
A function can be defined in terms of four
components:
– A domain set, which is the set of objects to which the
function can be applied;
– A range set, which is the set containing all objects
that can result from an application of the function;
– A definition, which is the specification of how a range
element is determined from a domain element; and
– A name, which is a symbol dedicated to the function.
28
Functions (2)
A function can be viewed as a set of pairs
(x, y) such that yF(x) or as a subset of
the Cartesian Product XY:
F { (x, y) XY | yF(x) }
where means “is equivalent to” and
means “is contained in”. This is an
advantage of viewing a function as a set
for the study of the definition of functions
in programming languages.
29
An example
F(x) (x1) Mod 10
Indicating that, the function on the set of digits
(i.e., {0,1,2,3,4,5,6,7,8,9}) adds one to each digit
in modulo fashion This function can be
represented as the following set of pairs:
{(0,1),(1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,8),(8
,9),(9,0)}
or in set terminology as:
F { (x, y) digitdigit | y (x1) Mod 10}
30
An alternative representation
A function is
– F (x1, x2, … , xn, value)
where the last argument is called the
function result and uniquely can be
determined by the argument values of x1,
x2, … , xn.
31
Six independent components of FP
Set of primitives, which are predefined by the
language as the basic functions and
correspond to the built-in operations of
imperative languages.
Set of functional forms, which are functions
that accept functions as parameters to create
new functions.
Application operation, which is the built-in
mechanism for applying a function to its
arguments and producing a value as the result.
32
Six independent components (2)
Set of data objects, which are the allowed members of
the domain and range sets. Data objects consist of some
atomic type and the ability to construct some form of
aggregate objects from other objects.
Binding names to functions, which is a mechanism for
denoting names to the new functions being defined.
Dynamic storage management, which is an implicit
storage allocation and a garbage collection mechanism
because the functional languages do not provide
facilities for directly modifying the state of the storage for
a computation.
33
Orders of Functions
A function whose parameters and result
are all nonfunctional is called a first-order
function.
A function that has a functional parameter
or result is called a higher order
function.
34
Essential primitives
Selection operations: FIRST is used to extract
the first element of a sequence of elements,
LAST is used to extract the last element, and
TAIL is used to extract all the elements but the
first element.
– x1
– xn
– x2, … ,xn
FIRST: x1,x2, … ,xn
LAST: x1,x2, … ,xn
TAIL: x1,x2, … ,xn
Examples
– first: 3,2,4,6 3
– last: 3,2,4,6 6
– tail: 3,2,4,6 2,4,6
35
Essential primitives (2)
Structuring operations: Operations are used to combine,
dissect, or rearrange elements.
–
–
–
–
–
xn,x1, … ,xn-1 ROTR: x1,x2, … ,xn
x2, … ,xn,x1 ROTL: x1,x2, … ,xn
n LENGTH: x1,x2, … ,xn
x,x1,x2, … ,xn CONS: x,x1,x2, … ,xn
(ROTate Right)
(ROTate Left)
(LENGTH)
(CONstruct Sequence)
For example,
–
–
–
–
rotr: 3,2,4,6 6,3,2,4
rotl: 3,2,4,6 2,4,6,3
length: 3,2,4,6 4
cons: 3,2,4,6 3,2,4,6
36
Essential primitives (3)
Arithmetic operations: Ordinary arithmetic operations
are applied to sequences of two elements to produce a
new element; + is used for addition, for subtraction, *
for multiplication, for division and, | for residue
operation. In functional arithmetic operations we use the
prefix form (e.g., :x,y instead of the usual Infix
notation (e.g., x y). The following are some function
definitions.
: x,y xy
: 3,2 5
: x,y xy
: 8,2 4
: x,y xy
: 3,2 6
: x,y xy
: 6,3 3
|: x,y x(xy)y
|: 9,2 1
37
Essential primitives (4)
Predicate operations: Operations are used to produce
results as truth values. We represent truth by T and false by
F in which a predicate function yields either T or F. In
addition to predicates for comparing numbers such as , ,
, , and , it provides predicates to inquire about sequences
and atoms. For example, in the following two examples, the
first returns a Boolean (T or F) from an inquiry of an atom
object, whereas the second returns a Boolean (T or F) from
an inquiry of a sentence.
ATOM:x if x is an atom then T else F
atom: a,b F
NULL:x if x nil then T else F
null: a,b F
eq: a,b F
eq: a,a T
: 4,2 T
38
Essential primitives (5)
Logical operations: Operations provide the
combination of the truth values. The operators are AND,
OR, and NOT.
AND: x,y T if both are T
and: T,F F
and: T,T T
OR: x,y T if one is T
or: T,F T
or: F,F F
NOT: x T if x is F
not: T F
not: F T
39
Essential primitives (5)
Identity operation: The function ID yields
the same element. For example,
x ID:x
id:a a
The most interesting features of FP
languages are their functional forms
because we are not used to functional forms
in conventional programming languages.
40
Program-Forming Operations
(PFO)
Composition
Construction
Insert
Apply to all
Condition
41
Composition
The functional form composition, denoted °, has the
syntax
(f °g): X f : ( g : X)
takes two functions as the arguments, and produces a
function equivalent to the application of the first
argument to the result of the application of the second
argument. For example, if we define two functions as
f(x) x 5 and g(x) x 4
then one composition form of f and g can be obtained:
h(x) f(g(x)), or
h(x) (x 4) 5 x 9
42
An example
The composition of the rotate left and
construct sequence operations applied to
a list of elements.
ROTL°CONS: x1, x2,x3,x4
ROTL: CONS: x1,x2,x3,x4
ROTL: x1,x2,x3 ,x4 x2,x3,x4,x1
43
Construction
The functional form construction, denoted [ ], has the
syntax
– [ f1, f2, … , fn ] : X f1 : X, f2 : X, … , fn : X
where it takes as arguments n functions, and yields a
function equivalent to applying each of the functions to
the same argument and forming a sequence of the
results. For example, if we have individual functions for
the maximum, minimum, and average of a sequence of
numbers, we define a construction as:
– [Maximum, Minimum, Average]
Then, for example, 5, 1, 3 is the produced result of
– [Maximum, Minimum, Average]:1,2,3,4,5
44
Insert
The functional form insert, denoted , has the following
syntax
f : X1, X2, … , Xn f : X1, f : X2, … , Xn
takes a function as an argument and yields a function
equivalent to applying the argument function to
successive elements of the sequence. For example,
f : if x is X1, then X1
else if x is the sequence X1, X2, … , Xn and n2
then f: X1, f: X2, … , Xn
45
An example
Thus +: 1,2,3,4,5 yields 15 as illustrated in
the following.
+:1,2,3,4,5 +:1, +:2,3,4,5
+:1, +:2, +:3,4,5
+:1, +:2, +:3, +:4,5
+:1, +:2, +:3, +:4, +:5
+:1, +:2, +:3, +:4, 5
+:1, +:2, +:3, 9
+:1, +:2, 12 +:1, 14 15
46
Apply to All
The functional form apply_to_all, denoted , has
the syntax
f: X1, X2, …, Xn f : X1, f : X2, … , f : Xn
This function can be illustrated in the following way.
f: if x is nil, then nil
else if x is the sequence X1, X2, …, Xn
then f:X1, f:X2, …, f:Xn
47
An example
This form takes a function as an argument and
yields a function equivalent to applying the
argument function to each element of the
sequence and forming a sequence of the
results. For example,
:2,3,4,5,6,2
yields 5,9,8, as illustrated in the following.
:2,3,4,5,6,2
:2,3,:4,5,:6,2 5,9,8
48
Condition
The functional form condition, denoted IF, takes
three functions as arguments and, depending on
the evaluation result of the first function as True
or False, returns the second or third function,
respectively. This function has the syntax
(IF function1 function2 function3):x
if function1:xT
then function2:x else
function3:x
if function1=x
then function2 else
function3
49
Examples
In the following two examples, evaluation of the
head of 2,3,5 with 2 and 3 yields the tail and
last element of the list, respectively.
– (IF FIRST:2,3,5 TAIL:2,3,5 LAST:2,3,5):2
– (IF 2 3,5 5):2 3,5
– (IF FIRST:2,3,5 TAIL:2,3,5 LAST:2,3,5):3
– (IF 2 3,5 5):3 5
50
Lisp Platform
http://www.lispworks.com/downloads/index
.html
51
Summary
Lambda Calculus
– Properties
– Ambiguity
– reductions
Principles of FP
– Components of a function
– Components of FPL
– PFO
•http://www.cs.cornell.edu/Courses/cs312/2001FA/lecture/lec25.htm
http://www.cs.uiowa.edu/~slonnegr/plf/Book/Chapter5.pdf
52