Download PowerPoint Presentation - AI and Automation

AI and Automation
Media and Culture
Lecture 9
John Lee
Introduction: what is “AI”?
• Two major areas where “AI” is talked about:
– engineering/automation
– studying, perhaps emulating, human cognition
• In practice, these do not often overlap
– (maybe they do in this video!)
– but at a theoretical level they share many issues and
approaches …
• Crucial general issue: how do we bring formal techniques to
bear in an informal world?
– “In logic, mathematics, and computer science, a formal system is a
formal grammar used for modelling purposes. Formalization is the
act of creating a formal system, in an attempt to capture the
essential features of a real-world or conceptual system in formal
language.” (Wikipedia, 26.10.05)
An unusual case …
Examples of formal systems
• Arithmetic (formal theory and calculus of numbers)
• Logic (formal theory and calculus of propositions)
• Natural language grammars
– Chomsky and all that …
• Shape grammars
– (http://www.mit.edu/~tknight/IJDC/)
• Music grammars
– (Lehrdahl, F. and R. Jackendoff. 1983. A Generative Theory of
Tonal Music, Cambridge, Mass: MIT Press)
•
•
•
•
Databases
Knowledge bases
Meteorological models (fluid dynamics)
Economic models
Formality and formalisation
• Central issue in AI and automation (but also much else):
– Computer is an entirely formal system, but world (and people)
seem not to be
– How to go from informal world to formal system, derive some
result, and then get back again without losing anything
important?
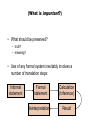
(What is important?)
• What should be preserved?
– truth?
– meaning?
• Use of any formal system inevitably involves a
number of translation steps:
Informal
statement
Formal
statement
Reinterpretation
Calculation
(Inference)
Result
Basic logical principles
• Analysis of natural language (e.g. English) argument:
– translation into logical form, application of rules, then
translation back …
• Compare analysis of arithmetical calculation:
–
–
–
–
Suppose 82 students get 175 pages of notes each …
Form is: result = A x B = 82 x 175 …
Calculation gives: result = 14,350
So we need (e.g.) to budget for 14,350 copies
Informal
statement
Formal
statement
Reinterpretation
Calculation
(Inference)
Result
… basic principles (continued)
• A simple argument (application of modus ponens):
– If the switch is down, (then) the light is on;
the switch is down …
<Informal>
– If P then Q; P …
<(semi-) formal translation>
P –> Q P
Q
<formal inference>
– … therefore Q
– So the light is on
<reinterpretation>
Informal
statement
Formal
statement
Reinterpretation
Calculation
(Inference)
Result
COMPUTATION
• What is it?
• Why is it important?
Turing's machine
• The first properly worked out theory of computation …
• an abstract formal machine
• head and tape:
– head can read, erase, write symbols, and move tape one square left or
right
– head is defined by a few rules e.g.: if the symbol below head is ‘1’,
erase it, write a ‘0’, and move one square left
– input for problem is posed by writing it on the tape at start time
– output from the problem is on the tape at ‘halt’ time
– given machine defines a mathematical function (set of pairs of
input/output)
Simple example …
• an adding machine — two numbers in ‘tally notation’
separated by blank
• machine finds blank, ‘moves 1s across blank’ until finished
• infinite (or extendable) machines — can always add more
tape
Head
I
I
I
I
I
I
I
I
I
I
I
I
I
I
Universal machines
• a Universal machine can mimic any other Turing machine
• mimicked machine is encoded as number on U-machine's tape,
along with input for particular problem for mimicked machine
• U-machine can mimic the encoded machine solving the problem
<emulation>
• Turing then proved that there are functions which U-machine
can't compute …
– notably the ‘halting problem’: will machine halt when computing a
given function?
• … but developed the “Church-Turing” thesis that:
– a Universal Turing Machine can compute anything that can be
computed at all
• A staggering result from such a simple starting point!
• Corollary: some functions cannot be computed at all …
What is so important about Turing's
machine?
• active head vs. passive memory: treating program as
data
• hardware vs. software — distinguish abstract
computation from physical implementation
• can consider large range of alternative implementations
• establishes an abstract ‘informational’ level for
describing behaviour
– in fact, engineered computers are like Turing machines with
random access memory (RAM) (not infinite, unfortunately)
– and vastly complicated heads called central processing units
(CPUs)
– (these are technically “von Neumann” machines)
Automation of logical proof
• Sometimes proofs can be computable
• Even whole systems of proof
• Programming languages can be based on this
– E.g. Prolog
– A language based on theorem proving from
• FACTS and
• RULES
Compare:
factorial(1, 1).
factorial(Num, Factorial):M is Num-1,
factorial(M, FM),
Factorial is FM*Num.
(Declarative)
int factorial(int x) {
if (x == 1) return x;
else return x*factorial(x-1);
}
(Procedural)
Applications of AI
• What can we do with these ideas, and how?
General applications of AI (1):
Representation of knowledge
• (Contrast with data …
– knowledge is richer and includes means of deriving consequences)
• Rule-based systems
–
–
–
–
Cf Prolog: represent everything with facts and rules …
… then derive consequences by proof.
Assumes all knowledge can be captured this way
As in traditional expert systems
• Case-based reasoning
– Suppose that systems of rules will be too complicated …
– Instead store cases that have worked in the past,
– and some rules for working out how to re-use these
General applications of AI (2):
Approaches to formal semantics
• Meaning as truth conditions
• What does the world have to be like for a sentence to
be true?
• Provides semantics for simple systems like
propositional or predicate calculus
• Can be elaborated for use with natural languages, e.g.
– Consider the world at other points in time
– Consider other possible worlds
• What can this approach not capture?
Understanding humans
• How can we use computational theories to
understand the workings of the human mind?
• Is this an illusory goal?
Representational theories of mind
• The Computational Metaphor: hard and soft AI
• Contrast between focus on representation and focus
on behaviour
• What is "intelligence"?
– Is it what you can do or is it how you do it?
• The Turing Test
– The Loebner Prize – http://hps.elte.hu/~gk/Loebner/TT.html
– Eliza
• Dennett, the "Intentional Stance" and instrumentalism
– Idea that notions like “intelligence” are attributed
– Linked to anti-essentialism and anti-realism
Connectionist approaches and
non-representationalism
• Connectionism, or “neural-net”-based theories
– Distributed processing
– No explicit locus of symbols or syntactic structures
• Emergence
– The sum of a system can be more than its parts
• Environmental embedding and situated action
– Lucy Suchman
• Compare philosophical approaches of, e.g.
– Heidegger (existential embedding)
– Wittgenstein (social embedding)
Two classic critiques
• Dreyfus – phenomenology & Heidegger –
Winograd & Flores
– Fundamentalist anti-representationalism
– Strong AI is impossible in principle
• Searle – the “Chinese Room”
– More pragmatic argument
– Homunculus knows nothing, hence
system cannot be a locus of
understanding
– Extended as claim that no mere
symbol-processing system could ever
“understand” anything at all
– Claimed to be an “in-principle”
argument
近义词
AI in practical use
• What is actually being done using these ideas?
Practical considerations:
AI as software engineering
• Various general application fields
– Expert systems
• Either rule-based or case-based
– Verification systems
• To prove e.g. properties of safety-critical software
– Language engineering – LSA – etc.
• Used e.g. to mark essays
• Information extraction, e.g. as in Edinburgh-Stanford Link
• Combined maybe with text/speech generation: www.dj4me.com
– Dialogue systems
• Increasingly multimodal: speech, gesture, etc.
• Telephone sales etc. applications; commercial “chatbots”
• Entertainment, e.g. the BBC’s Jamie Kane
– ITSs
• Will teachers be replaced by computers?
• Importance of the social …
Design/architecture applications
• Representation of design knowledge (contrast with
Schön!)
– Cf. Coyne et al. Knowledge-Based Design Systems
•
•
•
•
•
•
•
Intelligent information design and presentation
Automated musical composition
Shape grammars (http://www.mit.edu/~tknight/IJDC/)
CBR
Building performance evaluation systems
Standardisation and automation in construction
Issues of “prescriptiveness” …