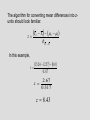* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
History of statistics wikipedia , lookup
Foundations of statistics wikipedia , lookup
Taylor's law wikipedia , lookup
Degrees of freedom (statistics) wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Omnibus test wikipedia , lookup
Statistical hypothesis testing wikipedia , lookup
Misuse of statistics wikipedia , lookup
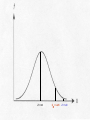
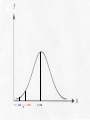
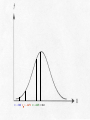
T- and Z-Tests for Hypotheses about the Difference between Two Subsamples Random samples, partitioned into two independent subsamples (e.g., men and women). Question: Are the means of some variable (such as salary) significantly different between the two subsample? Key: The sampling distribution of all theoretically possible differences between subsample means. For large samples (i.e., when the Central Limit Theorem holds), this sampling distribution of mean differences is normally shaped; for smaller samples, the sampling distribution takes the shape of one of the Student’s t distributions, identified by degrees of freedom. The key is: The difference between two means is a single value. In the case of these so-called “means difference tests,” the null hypothesis is that the means in general (i.e., in the universe) do NOT differ. Symbolically, H0: 2 - 1 = 0.00 There are two possible alternate hypotheses: nondirectional; H1: 2 - 1 0.0 and directional, either H1: 2 - 1 > 0.0 or H1: 2 - 1 0.0 In the 1984 General Social Survey, female respondents were asked whether or not their mothers had attended college. Then these female respondents were asked about their own education levels. A reasonable (alternate) hypothesis (H1) would be: Women whose mothers attended college will themselves have more formal education than women whose mothers did not attend college. Thus, our two hypotheses are : H1: 2 - 1 > 0.0 H0: 2 - 1 = 0.00 Dividing respondents into women whose mothers attended college and women whose mothers did not led to the calculation of the following statistics for the two subsamples: Mothers ATTENDED College _ Y2 = 15.24 s22 = 6.57 N2 = 90 Mothers DID NOT Attend _ Y1 = 12.57 s12 = 9.82 N1 = 359 Notice that the sample means DO in fact differ. This is NOT the question. Because these two subsamples combined exceed 100, we know that the Central Limit Theorem applies. We can convert the difference between the value of the sample mean differences and the presumed value of the mean difference in the universe under the null hypothesis (i.e., 0.0) to z-values by using the estimated standard error of the difference (the standard deviation of the sampling distribution of sample mean differences). Recall that in general standard errors are estimated by dividing the standard deviation of the sample by the square root of the sample size, ̂ sY N However, in the case of this means difference test, we have TWO subsamples and thus TWO standard deviations (actually variances in this example), one for each subsample. What do we do? Simply combine the two subsample variances, as follows: ˆ y 2 y1 2 2 2 1 s s N 2 N1 With the information from above, this means 6.57 9.82 ˆ y2 y1 90 359 ˆ y 2 y1 ˆ y ˆ y 2 2 y1 0.073 0.0274 0.1004 y1 0.317 The algorithm for converting mean differences into zunits should look familiar: Y z 2 Y1 2 1 ˆ Y Y 2 1 In this example, 15.24 12.57 0.0 z 0.317 2.67 z 0.317 z 8.43 Selecting alpha = 0.05 for a one-tailed test and looking for a critical value in Appendix 1 (pp. 540-542), we again interpolate between 0.4495 and 0.4505, making z = 1.645. Since 8.43 is GREATER THAN the critical value of 1.645, we REJECT the null hypothesis at the 0.05 level and conclude that IN GENERAL women whose mothers attended college have higher education levels than women whose mothers did not attend college. Selecting alpha = 0.05 for a one-tailed test and looking for a critical value in Appendix 1 (pp. 540-542), we again interpolate between 0.4495 and 0.4505, making z = 1.645. Since 8.43 is GREATER THAN the critical value of 1.645, we REJECT the null hypothesis at the 0.05 level and conclude that IN GENERAL women whose mothers attended college have higher education levels than women whose mothers did not attend college. Z = 0.0 Z = 1.645 Z = 8.43 For random samples whose combined size is less than 120, we cannot assume that the sampling distribution of mean differences will be normally shaped. This is because the Central Limit Theorem doesn't hold with samples this small. Student's t distributions must be used instead. The only new wrinkle here is that the standard error of the difference cannot be estimated as above. The sample standard deviations must be pooled in a way that is sensitive to the impact of even slight differences in small numbers. Consider the following example: The 63-city data set that we are using this semester has been divided into two subsamples, one consisting of SUNBELT cities and the other of FROSTBELT cities. The question is: Did frostbelt cities lose population at a higher rate than sunbelt cities in the fifteen years between 1960-1974? Sample statistics are these: Frostbelt Cities _ Y2 = - 4.14 s22 = 9.98 N2 = 37 Sunbelt Cities _ Y1 = 2.84 s12 = 57.61 N1 = 26 In the sample, frostbelt cities clearly lost population (population change - 4.14 percent) at a greater rate than sunbelt cities (which GAINED population, + 2.84 percent). The question is, is this sample difference sufficient to infer a similar trend in the universe of American cities? Our alternate hypothesis is that in general frostbelt cities lost population at a higher rate than sunbelt cities, hence H1: 2 - 1 < 0.0 In other words, we expect 2 to be a larger negative number than 1. Notice again that the presence of the “less than” sign (“<”) dictates a one-tailed test, this time in the left-hand tail where negative mean differences are located. Our null hypothesis is that there is no difference in the rates of population change, or H0: 2 - 1 = 0.00 Since the subsample sizes are relatively small, we can't simply slam the standard deviations together to estimate the standard error of the difference. We must weight the subsample standard deviations (actually the subsample variances) by the size of the subsamples (actually by the number of degrees of freedom in the subsamples) before estimating the standard error. This is called pooling. s pooled [( N 2 1) s ( N1 1) s ] ( N 2 N1 2) 2 2 In this example, s pooled [(37 1)(9.98) (26 1)(57.61)] (37 26 2) s pooled s pooled [(36)(9.98) (25)(57.61)] 61 359.280 1440.250 61 2 1 s pooled 1799.53 61 s pooled 29.500 s pooled 5.431 Now we can use this “pooled” constant to estimate the standard error of the difference. The estimation is ˆ y2 y1 where s = spooled s2 s2 1 1 s N 2 N1 N 2 N1 ˆ y ˆ y 2 2 y1 ˆ y 2 ˆ y y1 1 1 37 26 (5.431) 0.027 0.039 y1 2 (5.431) y1 ˆ y 2 (5.431) 0.066 (5.431)(0.257) y1 1.396 Now we have the value of the standard error of the difference, 1.396; this is our “currency exchange rate” that will allow us to determine the value of the test statistic. The algorithm should look familiar: Y t 2 Y1 2 1 ˆ Y Y 2 1 In this example, [( 4.14) (2.84)] 0.0 t 1.396 6.98 t 1.396 t 5.00 We now know that location - 6.98 on the sampling distribution converts to a t-location of - 5.00 on the underlying X-axis. But what is the exact SHAPE of this sampling distribution? It is the Student’s t distribution with 61 degrees of freedom. We have 63 cities selected randomly, but the cities have been subdivided into two subsamples (frostbelt and sunfelt cities). The 37 frostbelt-city subsample has 36 degrees of freedom (37 - 1 = 36), and the 26 sunbelt-city subsample has 25 degrees of freedom (26 - 1 = 25). More generally, the number of degrees of freedom in the t-test is df = N2 + N1 - 2 Consulting Appendix 2 (p. 543) in search of the critical value for df = 61, we once again find only critical values for df = 60 and for df = 120. Let's assume that we want to make our test with alpha = 0.05. We could interpolate, by finding the value that is 1 / 60th of the way from 1.671 to 1.645. This value is extremely small and would round back to 1.671. But we need the critical value for the left (negative) tail, and Appendix 2 has only values for the right (positive) tail. Because Student's t distributions are all SYMMETRICAL, we simply add the negative sign to 1.671. Thus, our critical value is t0.05 = –1.671. Since t = - 5.00 is GREATER THAN t = - 1.671, this means that our sample difference lies INSIDE the region of rejection in the left-hand tail. Thus, we REJECT the null hypothesis at the 0.05 level and conclude that in general frostbelt cities in the U.S. probably did lose population at a greater rate than sunbelt cities in the period 1960 and 1974. t = - 5.00 t = - 1.671 t = 0.0 Using SAS to Produce T-Tests libname old 'a:\'; libname library 'a:\'; options nonumber nodate ps=66; proc ttest data=old.cities; class agecity2; var manufpct; title1 'An Example of a T-Test'; title2 'SAS Version 8.1'; title3 'PPD 404'; run; An Example of a T-Test SAS Version 8.1 PPD 404 The TTEST Procedure Statistics Variable Class N MANUFPCT MANUFPCT MANUFPCT Newer Older Diff (1-2) Lower CL Mean Mean Upper CL Mean Lower CL Std Dev Std Dev Upper CL Std Dev Std Err 22.928 20.1 -2.706 26.526 23.92 2.6063 30.125 27.74 7.9183 8.9262 7.2268 8.7659 10.949 9.2553 10.316 14.165 12.875 12.536 1.7761 1.8511 2.6565 38 25 T-Tests Variable Method Variances MANUFPCT MANUFPCT Pooled Satterthwaite Equal Unequal DF t Value Pr > |t| 61 57.1 0.98 1.02 0.3304 0.3139 Equality of Variances Variable Method MANUFPCT Folded F Num DF Den DF F Value Pr > F 37 24 1.40 0.3897 Reject the null hypothesis (H0) when either: 1. the value of the statistical test (2, z, t, F', or F) exceeds the critical value at the chosen -level; or, 2. the p-value for the statistical test is smaller than the chosen value of . Do NOT reject the null hypothesis (H0) when either: 1. the value of the statistical test (2, z, t, F', or F) is less than the critical value at the chosen -level; or, 2. the p-value for the statistical test is greater than the chosen value of . t = - 5.00 t = - 1.671 t = - 0.25 t = 0.0 Exercise 1 Means Difference Test In the 1984 General Social Survey (GSS), 234 male respondents with at least some college had a mean occupational prestige score of 47.49 (with a variance of 213.28). In contrast, 351 male respondents with only a high school education or less had an average occupational prestige score of 34.04 (with a variance of 132.30). Test the null hypothesis (H 0) that there is no statistically significant difference in occupational prestige between these two groups. Assume that = 0.05. Perform a two-tailed test. Make your decision regarding the null hypothesis using z-values in Appendix 1 (“Proportions of Area under Standard Normal Curve"), pp. 540-542. 1. What is the value of the standard error? 2. What is the value of Z? 3. What are the values of Z at the 2.5 percent and 97.5 percent areas under the normal curve? 4. Do you reject or accept this null hypothesis? Exercise 1 Answers Means Difference Test 1. What is the value of the standard error? 2. What is the value of Z? 11.850 3. What are the values of Z at the 2.5 percent and 97.5 percent areas under the normal curve? 1.96 Do you reject or accept this null hypothesis? Reject 4. 1.135 Exercise 2 Two Independent Samples t-test In an experiment to determine the effects of hunger on handeye coordination, the following results, representing the number of tasks completed success-fully, were obtained: Experimental Group (#1) (Hungry) Mean S.D. N 14.0 2.449 10 Control Group (#2) (Normal) 19.0 3.873 12 Calculate the estimated standard error of the difference, obtain the value of t, and test the hypothesis that the normally-fed (control) group performed better than did the hungry (experimental) group. Use Student's t distribution (Appendix 2, p. 543), and assume that = 0.05. Perform a one-tailed test. Exercise 2 (continued) Two Independent Samples t-test 1. Expressed symbolically, what is the alternate hypothesis? 2. Expressed symbolically, what is the null hypothesis? 3. What is the value of the standard error? 4. What is the value of t? 5. How many degrees of freedom in this problem? 6. What is the critical value of tdf? 7. Do you reject or accept the null hypothesis? Exercise 2 Answers Two Independent Samples t-test 1. Expressed symbolically, what is the alternate hypothesis? 2 - 1 > 0.0 2. Expressed symbolically, what is the null hypothesis? 2 - 1 = 0.0 3. What is the value of the standard error? 1.416 4. What is the value of t? 3.530 5. How many degrees of freedom in this problem? 6. What is the critical value of tdf? 7. Do you reject or accept the null hypothesis? Reject 20 + 1.725