Download Decibel notes

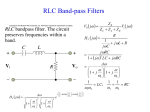
Digital and Interfacing
Systems.
Ceng 306.
Decibel (dB)
Supplement
Prepared by Mike Crompton (Revised 31 March 2005)
Decibel (dB)
A decibel is one tenth of a ‘Bel’. The Bel is the unit used to measure the response of the
human ear to sound intensity. It may be thought of as a ‘quantity of sound’. The human
ear responds to sound on a logarithmic scale, thus the dB scale is also logarithmic. It is
most often used to compare two levels of intensity, rather than give absolute values of
intensity.
One common use of dB’s in electronics is to compare different levels of power (Watts).
For example the power output to power input ratio of an amplifier (Power Gain). The
relationship between dB and Watts is:
dB = 10 Log10 Watts.
To determine the power ‘Gain’ of an amplifier, the ratio of power out to power in is:
Power Gain = Power Out / Power In
and to express this in dB:
dB Gain = 10 Log (Power Out / Power In).
The gain of an amplifier can also be expressed as a ratio of Voltage Out divided by
Voltage In.
Since there is a direct relationship between Watts (Power) and Voltage (or Current), the
voltage (or current) gain can also be expressed in dB.
dB Gain = 20 Log (Voltage Out / Voltage In)
Note: The above formula is only correct if the input and output impedance is the same.
Very often this is not the case and an error will result. Since the error is only significant
when the difference in impedance is very large, we will ignore it when calculating RC or
RL filter gain.
Converting Voltage Gain (or loss) to dB is particularly useful when expressing the loss of
signal when fed through a passive RC Hi or Lo pass filter. To use a low pass filter as an
example, we say that as we increase frequency, VC , which is also VOUT , drops. When it
drops to 0.707 times VIN we have reached the cut-off frequency (FC). All frequencies
above this will be greatly ‘attenuated’ (reduced, negative gain) and considered as
unusable. This 0.707 times VIN is the half power level (50% of Watts in) and is actually
equal to a drop of 3dB, or –3dB. Thus a 3dB change is equal to the power being halved or
doubled.
e.g. If VIN is 12V and VOUT is 12 x 0.707, dB Gain is:
dB Gain = 20 Log (VOUT / VIN) = 20 Log [ (12 x 0.707) / 12] = -3.01 dB
2
or if power in is 3Watts and power out is 6Watts, dB gain is:
dB Gain = 10 Log (POUT / PIN) = 10 Log (6/3) = 3.01 dB
Continuing with a Lo-Pass filter, at frequencies below FC the loss, attenuation or negative
gain changes from slightly below 0dB at 0 Hz to –3dB at FC. From that point on, further
increases in frequency produce a –20dB change for every decade of increase. i.e. At 10
times FC attenuation is –20dB, at 100 times FC attenuation is –40dB and at 1000 times FC
it is –60dB etc. See the ‘Bode Plot’ below.
For a Hi-Pass filter the –20dB change occurs as the frequency drops below FC. i.e. At
1/10 FC attenuation is –20dB, at 1/100 FC it is –40db and at 1/1000 FC it is –60dB.
dB
Filter output in dB.
0dB
-3dB
-20dB
-40dB
-60dB
Freq.
Fc
Fc x 10
Fc x 100
Fc x 1000
Bode plot of Low-Pass filter dB output Vs frequency
A Hi-Pass filter Bode plot would be a mirror image of the low-pass plot above.
Working with dB’s can at first be intimidating, but with practice the benefits soon
become obvious. These include the ability to represent large gain values with relatively
small dB values, and to determine overall gain of multi-stage amplifiers by simply adding
the individual dB gains.
3